Поиск целочисленного решения двойственной задачи.

Составим задачу, двойственную к исходной задаче (9) – (10). Мы получим следующую задачу на минимум:

 

g (U) = 4u₁ +12u₂ + 4u₃ ® min, (12)

u ₁ + 5 u ₂ +2u₃ 2,

3u₁ - u₃ ³ 1, (13)

– 2u₁ -u₂ +3u₃ ³ – 3,

u ₁, u _2, u ₃³ 0.

 

Обозначим через – оптимальный опорный план двойственной задачи (12) – (13) воспользуемся теоремой о равновесии.

1. Подставим координаты оптимального опорного плана в систему ограничений (10):

 

 

Так как второе ограничение превратилось в строгое неравенство, то соответствующая компонента оптимального опорного плана двойственной задачи равна нулю (). Осталось найти компоненты и . Для этого воспользуемся второй частью теоремы о равновесии.

2. Так как первая и вторая компоненты оптимального опорного плана строго больше нуля (), то соответствующие (первое и второе) ограничения двойственной задачи, при подстановке в них компонент оптимального плана , обратятся в равенства. Данные равенства дают нам систему линейных уравнений для нахождения и :

 

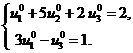(14)

 

Подставляя в систему (14) уже найденное значение , получим систему двух уравнений с двумя неизвестными:

 

(15)

 

Решением данной системы является . Таким образом, мы нашли оптимальный опорный план двойственной задачи: . При этом экстремальные значения функций цели взаимно-двойственных задач совпадают:

.

Теперь по двойственной задаче найдем опорный план, который соответствует целочисленному решению основной задачи(9)-(10).

Алгоритм нахождения целочисленного оптимального опорного плана такой же.

Через обозначим целочисленный оптимальный опорный план двойственной задачи (12) – (13) воспользуемся теоремой о равновесии.

3. Подставим координаты целочисленного оптимального опорного плана в систему ограничений (10):

Так как первое и второе ограничения превратились в строгие неравенства, то соответствующие компоненты оптимального опорного плана двойственной задачи равны нулю (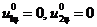). Осталось найти компоненту . Для этого воспользуемся второй частью теоремы о равновесии.

Так как первая компонента целочисленного оптимального опорного плана строго больше нуля, то соответствующее (первое) ограничение двойственной задачи, при подстановке в него компонент целочисленного оптимального плана , обратится в равенство. Получим уравнение , из которого легко найти , подставляя найденные ранее значения 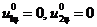. Т.е. =1.

Таким образом, мы нашли целочисленный оптимальный опорный план двойственной задачи: . При этом экстремальные значения функций цели взаимно-двойственных задач совпадают:

.

Составим исходную таблицу к задаче (12)-(13)(предварительно сделав ее на максимум и ограничения вида ). После двух шагов модифицированных жордановых исключений, приходим к оптимальному опорному плану двойственной задачи, записанному в таблице 12. Полученное оптимальное решение u₁=4/7, u₂=0, u₃=5/7 нецелочисленно, поэтому приступаем к отысканию целочисленного плана двойственной задачи. Проведем его двумя путями: обычным симплекс-методом и двойственным.

Выбираем среди свободных членов дробный. Так как в нашем

примере все они дробные, берем любой из них, например 5/7 из

первой строки.

Таблица 12

	-v2 -u2 -v1
u3= u1= v3=	1/7 15/7 -3/7 -2/7 5/7 -1/7 1 6 -1	5/7 4/7
g=	4/7 4/7 16/7	-36/7

 

По формулам (4) находим дробные доли коэффициентов b выбранной первой строки:

Дополнительное ограничение будет иметь вид

Вводим это ограничение в задачу и получаем табл.13.

 

Таблица 13

	-v2 -u2 -v1
u3= u1= v3= s1=	1/7 15/7 -3/7 -2/7 5/7 -1/7 1 6 -1 -1/7 -1/7 -4/7	5/7 4/7 -5/7
g=	4/7 4/7 16/7	-36/7

 

 

План, записанный в таблице, стал недопустимым. Принимаем за разрешающий элемент число (-4/7), делаем шаг модифицированных жордановых исключений и приходим к таблице 14.

Таблица 14

	-v2 -u2 -s1
u3= u1= v3= v1=	1/4 9/4 -3/4 -1/4 3/4 -1/4 5/4 25/4 -7/4 1/4 1/4 -7/4	5/4 4/7 21/4 5/4
g=	0 0 4	-8

 

 

Найденное решение оптимально, но не целочисленно. Берем дробный свободный член 5/4 снова в первой строке и по коэффициентам этой строки формулируем аналогично предыдущему второе дополнительное условие. Практически оно составляется прямо в таблице, поскольку дробные доли коэффициентов легко вычисляются в уме. Записывать их надо со знаком минус (табл.15

 

Таблица 15

	-v2 -u2 -s1
u3= u1= v3= v1= s2=	1/4 9/4 -3/4 -1/4 3/4 -1/4 5/4 25/4 -7/4 1/4 1/4 -7/4 -1/4 -1/4 -1/4	5/4 3/4 21/4 5/4 -1/4
g=	0 0 4	-8

 

План, записанный в табл. 15, снова является недопустимым.

Выбираем разрешающий элемент (-1/4) и делаем еще один

шаг (табл. 16). План, полученный в табл. 16, является допустимым, оптимальным и целочисленным.

Таблица 16

	-s2 -u2 -s1
u3= u1= v3= v1= v2=	1 2 -1 -1 1 0 5 5 -3 1 0 -2 -4 1 1
g=	0 0 4	-8

 

Таким образом,

 

 

ГЛАВА II

ТРАНСПОРТНАЯ ЗАДАЧА

 

§1. Математическая постановка задачи.

Общая постановка транспор­тной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления А₁, А₂,..., А_m в n пунктов назначения В₁, В₂,..., В_n. При этом в качестве крите­рия оптимальности обычно берется либо минимальная стоимость пере­возок всего груза, либо минимальное время его доставки. Рассмотрим транспортную задачу, в качестве критерия оптимальности которой взята минимальная стоимость перевозок всего груза. Обозначим через cij тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через a_i – запасы груза в j-м пункте отправления, через bj - потребности в грузе в j-м пункте назначения, а через х_ij - количество единиц груза, перевозимого из i-го пункта отправления в j-й пункт назначения. Тогда математическая постановка транспортной задачи состоит в определении минимального значения функции

F= (1)

при условиях

=b_j (j=1,…,n), (2)

=a_i (i=1,…,m), (3)

x_ij≥0 (i=1,…,m; j=1,…,n). (4)

Поскольку переменные x_ij (i=1,…,m; j=1,…,n) удовлетворяют системам линейных уравнений (2) и (3) и условию неотрицательности (4), обеспечиваются доставка необходимого количества груза из всех пунктов отправления, а также исключаются обратные перевозки.

Планом транспортной задачи называется всякое неотрицательное решение систем линейных уравнений (2) и (3), определяемое матрицей Х=(х_ij) (i=1,…,m; j=1,…,n).

Оптимальным планом транспортной задачи называется план Х*=(х^*_ij) (i=1,…,m; j=1,…,n), при котором функция (1) принимает свое минимальное значение.

Обычно исходные данные транспортной задачи записывают в виде табл.1.

Таблица 1

Пункты отправления	Пункты назначения	Запасы
В1	...	Вj	…	Вn
A1	с11 х11	...	с1j х1j	...	с1n х1n	a1
…	...	...	...	...	...	...
Ai	ci1 хi1	...	cij хij	...	cin хin	ai
…	…	...	…	...	…	…
Am	cm1 хm1	...	cmj хmj	...	cmn хmn	am
Потребности	b1	...	bj	...	bn

 

Очевидно, общее наличие груза у поставщиков равно , а общая потребность в грузе в пунктах назначения равна единиц. Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т.е.

= (5)

то модель такой транспортной задачи называется закрытой. Если же указанное условие не выполняется, то модель транспортной задачи называется открытой.

Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т.е. чтобы выполнялось равенство (5).

В случае превышения запаса над потребностью, т.е. при > ,вводят фиктивный (n+1)-й пункт назначения с потребностью b_n+1= - и соответствующие тарифы считают равными нулю: с_in+1=0 (i=1,...,m). Полученная задача является транспортной задачей для которой выполнено равенство (5).

Аналогично, при < вводят фиктивный (m+1)-й пункт отправления с запасом груза а_m+1= - и соответствующие тарифы полагаются равными нулю: с_m+1j=0 (j=1,…,n). Этим задача сводится к транспортной задаче с закрытой моделью, из оптимального плана которой получается оптимальный план исходной задачи. Поэтому в дальнейшим будем рассматривать только закрытую модель транспортной задачи. Если же модель конкретной задачи является открытой, то, исходя из сказанного выше, перепишем таблицу условий задачи так, чтобы выполнялось равенство (5).

Число переменных х_ij в транспортной задаче с m пунктами отправления и n пунктами назначения равно n+m. Так как мы предполагаем, что выполняется условие (5), то число линейно независимых уравнений равно n+m –1. Следовательно, опорный план транспортной задачи может иметь не более n+m-1 отличных от нуля неизвестных.

Если в опорном плане число отличных от нуля компонент равно в точности n+m-1, то план является невырожденным, а если меньше – то вырожденным.

Для определения опорного плана существует несколько методов. Три из них – метод северо-западного угла, метод минимального элемента и метод аппроксимации Фогеля – рассматриваются ниже. Мы рассмотрим наиболее эффективный из них, а именнно следующий.

Метод аппроксимации Фогеля. При определении опорного плана транспортной задачи методом аппроксимации Фогеля на каждой ите­рации по всем столбцам и по всем строкам находят разность между двумя записанными в них минимальными тарифами. Эти разности записывают в специально отведенных для этого строке и столбце в таблице условий задачи. Среди указанных разностей выбирают мини­мальную. В строке (или в столбце), которой данная разность соответс­твует, определяют минимальный тариф. Клетку, в которой он записан, заполняют на данной итерации.

Если минимальный тариф одинаков для нескольких клеток данной строки (столбца), то для заполнения выбирают ту клетку, которая расположена в столбце (строке), соответствующем наибольшей разнос­ти между двумя минимальными тарифами, находящимися в данном столбце (строке).

 

Пример.

Используя метод аппроксимации Фогеля, найти опорный план транспортной задачи. Четыре предприятия данного экономического района для производства продукции используют три вида сырья. Потребности в сырье каждого из предприятий соответственно равны 1120, 50, 190 и 110 ед. Сырье сосредоточено в трех местах его получения, а запасы соответственно равны 160, 140, 170 ед. На каждое из предприятий сырье может завозиться из любого пункта его получения.

 

 

Тарифы перевозок являются известными величинами и задаются матрицей

 

 

7 8 1 2

С = 4 5 9 8

9 2 3 6

 

Составить такой план перевозок, при котором общая стоимость перевозок является минимальной.

Решение.

Перепишем данные задачи в виде таблицы.

 

Пункты отправления	Пункты назначения	Запасы
В1	В2	В3	В4
А1
А2
А3
Потребности

 

Для каждой строки и столбца таблицы условий найдем разности между двумя минимальными тарифами, записанными в данной строке или столбце, и поместим их в соответствующем дополнительном столбце или дополнительной строке таблицы 1.

В строке А₁: 2-1=1

А₂: 5-4=1

А₃: 3-2=1

В столбце В₁: 7-4=3

В₂: 5-2=3

В₃: 3-1=2

В₄: 6-2=4

Вычислив все эти разности, видим, что наибольшая из них соответствует столбцу В₄. В этом столбце минимальный тариф записан в клетке, находящейся на пересечении строки А₁ и столбца В₄. Таким образом, эту клетку следует заполнить. Заполнив её, тем самым мы удовлетворим потребности пункта В₄.Поэтому исключим из рассмотрения столбец В₄ и будем считать запасы пункта А₁ равными 160-110=50 ед.

 

Таблица 1

Пункты отправле-ния	Пункты назначения	Запа-сы	Разности по строкам
В1	В2	В3	В4
А1								-	-	-	-
А2
А3										-	-
Потреб-ности
Разности по столбцам
			-
			-
		-	-
		-	-
-		-	-

 

После этого определим следующую клетку для заполнения. Снова найдем разности между оставшимися двумя минимальными тарифами в каждой из строк и столбцов и запишем их во втором дополнительном столбце и во второй дополнительной строке таблицы 1.Как видно из этой таблицы, наибольшая указанная разность соответствует строке А₁.Минимальный тариф в этой строке записан в клетке, которая находится на пересечении её с столбцом В₃.Следовательно, заполняем эту клетку. Поместив в неё число 50, тем самым предполагаем, что запасы в пункте А₁ полностью исчерпаны, а потребности в пункте В₃ стали равными 190-50=140 ед. Исключим из рассмотрения строку А₁ и определим новую клетку для заполнения. Продолжая итерационный процесс, последовательно заполняем клетки, находящиеся на пересечении строки А₃ и столбца В₃, строки А₃ и столбца В₂, строки А₂ и столбца В₂. В результате получим опорный план

0 0 50 110

Х = 120 20 0 0

0 30 140 0

 

При этом плане общая стоимость перевозок такова:

S=1*50+2*110+4*120+5*20+2*30+3*140=1330.

Как правило, применение метода аппроксимации Фогеля позволяет получить либо опорный план, близкий к оптимальному, либо сам оптимальный план. Найденный нами опорный план является оптимальным.

 

В задачах о назначениях мы всегда имеем дело с вырожденными оптимальными планами, у которых ненулевых базисных компонент на 1 меньше, чем ненулевых. В такой ситуации наличие отрицательных оценок не говорит о неоптимальности опорного плана, а чаще всего зависит от расположения нулевых базисных компонент в соответствующей таблице транспортной задачи. В этом случае необходимо использовать такой метод построения первоначального оптимального плана, при котором базисные клетки выбирались бы наилучшим образом. Как известно таким методом является метод аппроксимации Фогеля, так как только опорный план, построенный по этому методу, имеет все положительные оценки и следовательно только он может быть признан оптимальным.

 

ЛИТЕРАТУРА

 

 

Основная

 

1. Замбицкий Д.К. Линейная алгебра и линейное программирование: Учеб. пособие / Д.К. Замбицкий, М.К. Замбицкий. – Кишинэу: Еврика, 1997. – 200 с.

2. Зуховицкий С. И. Линейное и нелинейное программирование / С. И. Зуховицкий, Л.И. Авдеева. – М.: Наука, 1967. – 352 с.

3. Полунин И.Ф. Курс математического программирования / И.Ф. Полунин. – Минск: Вышэйш. шк., 1968. – 253 с.

4. Полунин И.Ф. Курс математического программирования: Для с.-х. вузов по спец. «Экономика и организация сельского хоз-ва», «Бухгалтерский учет в сельском хоз-ве» и «Экономика и организация водного хоз-ва» / И.Ф. Полунин. – 3-е изд., доп. – Минск: Вышэйш. шк., 1975. –
380 с.

5. Полунин И.Ф. Курс математического программирования: Для с.-х. вузов по спец. «Экономика и организация сельского хоз-ва» и «Бухгалтерский учет в сельском хоз-ве» / И.Ф. Полунин. – Минск: Вышэйш. шк., 1970. – 318 с.

 

Дополнительная

 

1. Зуховицкий С. И. Линейное и выпуклое программирование / С.И. Зуховицкий, Л.И. Авдеева. – 2-е, изд. переработ. и доп. – М.: Наука, 1967. – 360 с.

2. Полунин И.Ф. Математическое программирование в землеустройстве: Учеб. пособие для землеустроит. фак. с.-х. вузов / И.Ф. Полунин. – Минск: Вышэйш. шк., 1968. – 253 с.

3. Еремин И.И. Теория линейной оптимизации / И.И. Еремин; Отв. ред. Л.Д. Попов; РАН. УРО. Ин-т математики и механики. – Екатеринбург, 1999. – 312 с.