y = b 0 + bi xi + bii xi 2 , (1)
напомним следующие факты:
1. Если bii > 0, то уравнение (1) описывает вогнутую функцию
(ветви параболы направлены вверх), а если bii < 0 – выпуклую.
2. Абсцисса вершины параболы (1) равна
xi в = − bi /2 bii.
Из этой формулы вытекают остальные свойства.
3. Если имеет место соотношение:
| bi | > 2| bii |, (2)
то вершина параболы находится вне диапазона варьирования фактора xi и, следовательно, уравнение (1) описывает монотонную функцию.
Если при этом bi > 0, то эта функция монотонно возрастающая, а при bi < 0 – монотонно убывающая.
4. При наличии соотношения
| bi | < 2| bii | (3)
функция (1) имеет экстремум внутри диапазона варьирования фактора xi: максимум при bii < 0 или минимум при bii > 0.
4. Пример выполнения РГР 2 и РГР 3
Применение В-плана второго порядка для исследования силовых характеристик процесса пиления древесины цепными моторными пилами
В эксперименте, выполненном в МЛТИ, был использован В-план с полным факторным планом (ПФП) в ортогональной части для исследования влияния пяти основных факторов на силовые характеристики процесса пиления древесины цепными моторными пилами. Матрица этого плана для нормализованных факторов приведена в столбцах табл. 4.
Эксперимент проводился на специальном пильном стенде. Исследуемые факторы, их интервалы и уровни варьирования приведены в табл. 5.
Формулы, связывающие нормализованные и натуральные обозначения (см. формулу (4.1) в [1] или (4.2.6) в [2]), будут в данном случае иметь следующий вид:
 x 1 = (D −0,9) / 0,3; x 2 = (v – 13,5) / 4,6;
x 1 = (D −0,9) / 0,3; x 2 = (v – 13,5) / 4,6;
x 3 = (F н – 90) / 30; x 4= (l – 20) / 10.
x 5= (L – 48) / 18;
Таблица 4
| № опыта | х 1 | х 2 | х 3 | х 4 | х 5 | 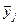 , Н , Н
| № опыта | х 1 | х 2 | х 3 | х 4 | х 5 |  ,Н ,Н
| |||
| +1 | +1 | +1 | +1 | +1 | −1 | +1 | −1 | +1 | −1 | |||||||
| +1 | +1 | +1 | +1 | −1 | −1 | +1 | −1 | −1 | +1 | |||||||
| +1 | +1 | +1 | −1 | +1 | −1 | +1 | −1 | −1 | −1 | |||||||
| +1 | +1 | +1 | −1 | −1 | −1 | −1 | +1 | +1 | +1 | |||||||
| +1 | +1 | −1 | +1 | +1 | −1 | −1 | +1 | +1 | −1 | |||||||
| +1 | +1 | −1 | +1 | −1 | −1 | −1 | +1 | −1 | +1 | |||||||
| +1 | +1 | −1 | −1 | +1 | −1 | −1 | +1 | −1 | −1 | |||||||
| +1 | +1 | −1 | −1 | −1 | −1 | −1 | −1 | +1 | +1 | |||||||
| +1 | −1 | +1 | +1 | +1 | −1 | −1 | −1 | +1 | −1 | |||||||
| +1 | −1 | +1 | +1 | −1 | −1 | −1 | −1 | −1 | +1 | |||||||
| +1 | −1 | +1 | −1 | +1 | −1 | −1 | −1 | −1 | −1 | |||||||
| +1 | −1 | +1 | −1 | −1 | +1 | |||||||||||
| +1 | −1 | −1 | +1 | +1 | −1 | |||||||||||
| +1 | −1 | −1 | +1 | −1 | +1 | |||||||||||
| +1 | −1 | −1 | −1 | +1 | −1 | |||||||||||
| +1 | −1 | −1 | −1 | −1 | +1 | |||||||||||
| −1 | +1 | +1 | +1 | +1 | −1 | |||||||||||
| −1 | +1 | +1 | +1 | −1 | +1 | |||||||||||
19 | −1 | +1 | +1 | −1 | +1 | −1 | ||||||||||
| −1 | +1 | +1 | −1 | −1 | +1 | |||||||||||
| −1 | +1 | −1 | +1 | +1 | −1 |
Таблица 5
| Наименование фактора | Обозначение | Интервал варьирования фактора | Уровень варьирования фактора | |||
| натуральное | нормализованное | нижний (−) | основной (0) | верхний (+1) | ||
| Снижение ограничителя подачи пильной цепи, мм | D | х 1 | 0,3 | 0,6 | 0,9 | 1,2 |
| Скорость резания, м/с | v | х 2 | 4,6 | 8,9 | 13,5 | 18,1 |
| Усилие надвигания пильного аппарата на образец, H | F н | х 3 | ||||
| Длина пропила, см | l | х 4 | ||||
| Рабочая длина пильного аппарата | L | х 5 |
Выходная величина эксперимента – усилие пиления F п, H.
Опыты проводились на древесине березы. Результаты предварительно проведенных экспериментов позволили принять гипотезу о нормальном распределении выходной величины. Проверка проводилась по критерию c2 Пирсона. На основе этих данных было рассчитано необходимое число n дублированных опытов, которое оказалось равным пяти.
Таблица 6
| Обозначение коэффициента регрессии | b 0 | b 1 | b 2 | b 3 | b 4 | b 5 | b 11 | b 22 | ||||||||||
| Оценка коэффициента регрессии | 219,46 | 29,98 | 3,94 | 52,82 | −8,87 | 21,18 | 2,9 | 0,4 | ||||||||||
| Пересчитанная оценка | 218,22 | 29,76 | 4,15 | 52,7 | −8,55 | 20,97 | − | − | ||||||||||
| Обозначение коэффициента регрессии | b 33 | b 44 | b 55 | b 12 | b 13 | b 14 | ||||||||||||
| Оценка коэффициента регрессии | −8,6 | −23,54 | −23,6 | 0,26 | 5,51 | 2,33 | ||||||||||||
| Пересчитанная оценка | − | -23,87 | -26,84 | − | 5,63 | − | ||||||||||||
| Обозначение коэффициента регрессии | b 15 | b 23 | b 24 | b 25 | b 34 | b 35 | b 45 | |||||||||||
| Оценка коэффициента регрессии | −3,19 | 1,68 | −1,51 | 2,01 | 3,53 | 4,76 | 8,58 | |||||||||||
| Пересчитанная оценка | −2,97 | − | − | − | 3,4 | 4,88 | 8,24 | |||||||||||
При реализации экспериментального плана в двух случаях пришлось несколько отступить от рекомендованных В-планом уровней варьирования факторов: в опытах № 18 и № 22 значения фактора l составили 26 см вместо 30 (соответственно значения x 4 в этих опытах фактически равны +0,6 вместо +1). В соответствии с найденным значением n =5 каждый опыт повторялся 5 раз. В седьмом столбце табл. 4 приведены значения усилий пиления, усредненные по пяти дублированным опытам каждой серии:
 .
.
По критерию Кохрена проверялась однородность дисперсий опытов:
G расч = 0,0875 < G табл = 0,12 для q = 0,05.
Это позволило оценить дисперсию воспроизводимости s 2 { y } как среднее арифметическое дисперсий опытов
 ;(2.2)
;(2.2)
s 2 { y } = 16455/42 = 391,8.
Связанное с ней число степеней свободы fy равно
fy = N (n −1) = 42 (5−1) = 168.
Из указанных выше отклонений реализованной матрицы от В-плана формулы (6.4) в [2] или (6.5) в [1] для расчета нормализованных коэффициентов регрессии оказались неприменимыми. Этот расчет был произведен на ЭВМ с помощью стандартной программы метода наименьших квадратов. Рассчитанные оценки коэффициентов регрессии приведены во второй строке табл. 6.
Оценки дисперсий и ковариаций коэффициентов регрессии находили с помощью формул (6.6) в [2] или (6.7) в [1], так как погрешности, вносимые отклонениями от В-плана в выражения, определяемые этими формулами, незначительны. Из последнего столбца табл.6.3 [1] или [2] имеем:
Т1 » 0,158; Т2»0,0332; Т3 »0,0294;
Т 4»0,5; Т5»−0,0918; Т6»0,0312.
По формулам (6.7) в [1] или (6.6) в [2] рассчитаны оценки:
s 2{ b 0} = (0,158/5) × 391,8 = 12,4;
s 2{ bi } = (0,0294/5) × 391,8 = 2,3;
s 2{ bii } = (0,408/5) × 391,8 = 32;
s 2{ bij } = (0,0312/5) × 391,8 = 2,44;
 |
Cov{ b 0, bii } = − (0,0332/5) × 391,8 = −2,6;
Cov{ bii, bij } = − (0,0918/5) × 391,8 = −7,18.
В соответствии с методикой оценки значимости коэффициентов регрессии определено табличное значение t -критерия Стьюдента для числа степеней свободы fy = 168. Из таблиц t -критерия (см.табл.1 Приложения в [1] или [2]) для q = 0,05 найдено t табл = 1,96. Для коэффициента b 0 имеем
s { b 0} =  =
= 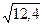 = 3,52; t табл s { b 0} = 1,96 × 3,52 = 6,9.
= 3,52; t табл s { b 0} = 1,96 × 3,52 = 6,9.
Отсюда видно, что для коэффициента b 0 соотношение (4.40) в [2] или (5.12) в [1] не выполняется, следовательно, он значим. Аналогичным образом установлена значимость всех линейных коэффициентов регрессии, а также коэффициентов b 44, b 55, b 13, b 15, b 34, b 35, b 45.
Значимые коэффициенты регрессии были пересчитаны на ЭВМ. Для этого в матрицу Х вводились только столбцы, соответствующие значимым коэффициентам. Вновь полученные оценки приведены в третьей строке табл. 6.
Таким образом, получено следующее уравнение регрессии:
y = 218,22 + 29,76 х 1 + 4,15 х 2 + 52,7 х 3 − 8,55 х 4 +
+20,97 х 5 – 23,87 х 42 – 26,84 х 52 + 5,63 х 1 х 3 – 2,97 х 1 х 5 + 3,4 х 3 х 4 + 4,88 х 3 х 5 + 8,24 х 4 х 5. (1)
Проверка его адекватности проведена согласно пункту 5.3 [1] или подпункту 4.5.3 [2].
Вычислены значения отклика  − по уравнению регрессии (2.4) для каждого опыта. Определена дисперсия адекватности s ад2 по формуле (4.47) [2] или (5.20) [1]: s ад2 = 541,16.
− по уравнению регрессии (2.4) для каждого опыта. Определена дисперсия адекватности s ад2 по формуле (4.47) [2] или (5.20) [1]: s ад2 = 541,16.
Вычислено расчетное F -отношение:
F расч = s ад2 / s 2 { y }; F расч = 541,16/391,8 =1,38,
которое сравнено с табличным F -отношением F табл (см. табл. 2 Приложения в [1] или [2]) для уровня значимости q и чисел степеней свободы f ад (числитель) и fу (знаменатель). Имеем f ад = N – p = 29, fу = 168. Для q = 0,05 F табл =1,5. Полученное соотношение F расч < F табл позволило принять гипотезу об адекватности регрессионной модели (1).
Приведем некоторые общие выводы, касающиеся анализа и интерпретации квадратичной модели. Для этого лучше всего пользоваться уравнением в нормализованных обозначениях факторов.
Займемся выборочным анализом уравнения. Очевидно, что зависимость y от каждого из факторов х 1, х 2, х 3 является линейной, так как соответствующие квадратичные члены отсутствуют. При этом можно утверждать, что с ростом величины D (снижение ограничителя подачи пильной цепи), соответствующей нормализованному фактору х 1, отклик возрастает всегда, при любых значениях остальных факторов. Для этого достаточно убедиться, что b 1 > 0 и b 1 >  . Действительно, имеем b 1 = 29,76 > 0 и 29,76 > 5,63 +2,97. Аналогично, с ростом скорости резания и усилия надвигания пильного аппарата на образец (нормализованные факторы х 2 и х 3 соответственно) усилия резания также всегда возрастают. Зависимости отклика от факторов х 4 и х 5 описываются уравнениями парабол, так как b 44 и b 55 отличны от нуля.
. Действительно, имеем b 1 = 29,76 > 0 и 29,76 > 5,63 +2,97. Аналогично, с ростом скорости резания и усилия надвигания пильного аппарата на образец (нормализованные факторы х 2 и х 3 соответственно) усилия резания также всегда возрастают. Зависимости отклика от факторов х 4 и х 5 описываются уравнениями парабол, так как b 44 и b 55 отличны от нуля.
Далее можно отметить, например, что наибольшее влияние фактора х 1 имеет место при х 3 = +1 и х 5 = −1. При этом ¶1 max = 29,76 + 5,63 + 2,97 = 38,36. Наибольшее влияние фактора х 5 проявляется в точке х 5 = −1; х 1 = −1; х 3 = х 4 = +1. При этих значениях |¶5 max |= | b 5| + 2| b 55| + | b 15| + | b 35| + | b 45| = 63,9. С другой стороны, парабола, которой описывается зависимость y = f (x 5), имеет, как будет показано ниже, максимум внутри диапазона варьирования фактора x 5, а в этой точке величина ¶5 равна нулю. Наибольшее влияние по показателю ¶ imax имеет фактор х 3: при х 1 = х 4 = х 5 = +1 |¶3 max |=66,61.
Рассмотрим семейство графических зависимостей y от х 5 при различных значениях х 4 и фиксированных уровнях остальных факторов. При этом появится эффект парного взаимодействия b 45, которое является наиболее значимым (см.1). Значения факторов х 1, х 2, х 3 зафиксировали на уровнях х 1 = х 2 = х 3 = −1, поскольку (как это показано в п. 6.6 [2]) при этих сочетаниях, а также при х 4 = +1 и х 5 = −1 достигается минимум усилий резания y. Подставив значения х 4 = +1 и х 1 = х 2 = х 3 = −1 в (2.4) получим
y = 101,42 + 27,3 х 5 –26,84 х 52. (2)
Можно построить эту параболу по точкам, но лучше предварительно выяснить ее «поведение» в интересующем исследователя диапазоне −1£ х 5 £ +1. Для этого уравнения b 55 = −26,84 < 0. Из соотношений (2.6) и (2.7) выполняется последнее. Поэтому данная парабола выпуклая и имеет максимум внутри диапазона варьирования, а именно в точке х 5в = −27,3/2Ч (-26,84) = 0,509. Это означает, что при соответствующем значении натурального фактора – рабочей длины пильного аппарата, имеет место максимум усилий резания. Подставив найденное значение х 5 = х 5в в уравнение (2), найдем величину этого максимума y в = 108,36. Для приближенного построения параболы можно воспользоваться еще тремя точками: х 5 = −1, y = 47,28; х 5 = 0, y = 101,42; х 5 = +1, y = 101,88 (кривая 1 на рис.1).
 |
|
Отметим, что от графиков, построенных для нормализованных факторов, очень просто перейти к натуральным обозначениям факторов. Для этого достаточно, не изменяя самой кривой, перейти к другому масштабу по оси абсцисс. Фактически вместо указанных на оси абсцисс значений нормализованного фактора –1 и +1 надо написать значения нижнего и верхнего уровней соответствующего натурального фактора (см. рис.1).
