РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

Архангельский государственный технический университет

 

 

ЭЛЕКТРОДИНАМИКА

Методические указания

К выполнению контрольного задания № 3

Для студентов-заочников

Инженерно-технических специальностей

Архангельск

Рассмотрены и рекомендованы к изданию методической комиссией

факультета промышленной энергетики

Архангельского государственного технического университета

29 октября 2003 г.

 

Составители:

Л.В. Филимоненкова, доц., канд. техн. наук;

Н.С. Самылова, ст. преп.;

И.В. Шульгин,ст. преп.

 

 

Рецензент

А.В.Соловьев, доц.,канд. техн. наук

 

УДК 530.1

Филимоненкова Л.В., Самылова Н.С., Шульгин И.В. Электродинамика: Методические указания к выполнению контрольного задания N3 для студентов-заочников инженерно-технических специальностей Архангельск: Изд-во АГТУ, 2004. – 45 с.

Подготовлены кафедрой физики АГТУ.

В указаниях даны общие рекомендации к решению задач по электромагнетизму, приведен необходимый справочный материал.

Предназначены для студентов-заочников инженерно-технических специальностей.

Ил. 35. Табл. 4. Библиогр. 8 назв.

 

 

ã Архангельский государственный технический университет, 2004

РЕКОМЕНДАЦИИ К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ

 

К выполнению контрольной работы следует приступить только после изучения материала, соответствующего данному разделу программы, внимательного ознакомления с примерами решения задач, приведенных в данном пособии по каждому разделу курса.

При выполнении контрольной работы необходимо руководствоваться следующими правилами.

1. Контрольная работа выполняется в обычной школьной тетради (каждая контрольная выполняется в отдельной тетради). Для замечаний рецензента на страницах тетради оставляются поля. Каждая следующая задача должна начинаться с новой страницы. Условия задач переписываются полностью без сокращений.

2. При решении задач следует пользоваться международной системой единиц (СИ). Все величины, входящие в условия задачи, выражаются в единицах этой системы.

3. Решения задач должны сопровождаться краткими, но исчерпывающими пояснениями, раскрывающими физический смысл употребляемых формул. В тех случаях, когда это возможно, дать чертеж, выполненный с помощью чертежных принадлежностей.

Если при решении задачи применяется формула, получаемая для частного случая, не выражающая какой-нибудь физический закон или не являющаяся определением какой-нибудь физической величины, то её следует вывести.

4. Решать задачу надо в общем виде, то есть выразить искомую величину в буквенных обозначениях величин, заданных в условии задачи. При таком способе решения не производятся вычисления промежуточных величин.

Получив решение в общем виде, сделать анализ его размерности. Для этого надо подставить в правую часть полученной рабочей формулы вместо символов величин обозначения единиц, провести с ними необходимые действия и убедиться в том, что полученная при этом единица соответствует искомой величине. Если такого соответствия нет, то это означает, что задача решена неверно.

5. В конце контрольной работы следует указать учебники и учебные пособия, которыми пользовались при решении задач.

6. Получив из университета проверенную работу, следует внимательно ознакомиться с замечаниями и указаниями рецензента. Если при выполнении контрольной работы были допущены ошибки, необходимо выполнить работу над ошибками в той же тетради и направить ее на повторную проверку.

7. После получения положительной рецензии студент обязан пройти собеседование по существу решенных задач. Итогом собеседования является зачет по контрольной работе.

8. Студентам, проживающим вблизи университета или филиалов и учебно – консультационных пунктов, рекомендуется прослушать курс лекции по физике, организуемых для студентов заочников, а также использовать очные консультации преподавателей кафедры физики.

 

Основные уравнения электродинамики

 

1. Электростатика

 

1.1. Закон сохранения электрического заряда:

,

где - алгебраическая сумма зарядов, входящих в изолированную систему; N - число зарядов.

1.2. Закон Кулона. Сила взаимодействия между двумя точечными зарядами и модуль этой силы F:

; ,

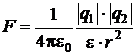где - радиус-вектор, соединяющий заряды; - электрическая постоянная, , e - диэлектрическая проницаемость среды, в которой расположены заряды q ₁ , q ₂.

 

Здесь коэффициент:

.

 

1.3. Характеристики электрического поля:

напряженность ; потенциал ,

где - сила, действующая на точечный положительный заряд q, помещенный в данную точку поля, -потенциальная энергия точечного положительного заряда q, помещенного в данную точку поля.

 

1.4. Напряженность и потенциал j поля точечного заряда q:

; ,

где - радиус - вектор, проведенный из точки, в которой расположен заряд q, до интересующей нас точки.

 

1.5. Напряженность и потенциал электрического поля, создаваемого заряженной сферической поверхностью радиусом R, несущей заряд q, на расстоянии r от центра сферы:

· внутри сферы (r<R)

E =0; ;

· на поверхности сферы (r=R)

; ;

· вне сферы (r>R)

; .

 

1.6. Распределение зарядов. Для упрощения математических расчетов во многих случаях бывает удобно игнорировать тот факт, что заряды имеют дискретную структуру и считать, что они “размазаны” определенным образом в пространстве. Другими словами, удобно заменить истинное распределение точечных дискретных зарядов фиктивным непрерывным распределением. При переходе к непрерывному распределению вводят понятие о плотности заряда — объемной r, поверхностной s, линейной t:

, ; , ; , ,

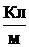где dq – заряд, заключенный в объеме dV, на поверхности dS, на длине dl.

1.7. Напряженность электрического поля, создаваемого бесконечно длинной равномерно заряженной нитью (или цилиндром) на расстоянии r от его оси:

,

где t-линейная плотность заряда.

1.8. Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью:

,

где s – поверхностная плотность заряда.

1.9. Поток Ф _Е вектора напряженности электрического поля:

· через плоскую поверхность, помещенную в однородное поле,

,

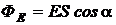· через произвольную поверхность S, помещенную в неоднородное поле,

Рис. 1.

,

где вектор, модуль которого равен dS, а напрвление совпадает с направлением единичного вектора нормали к элементу поверхности; a - угол между вектором напряженности и нормалью к элементу поверхности (рис.1).

1.10. Теорема Остроградского-Гаусса. Поток вектора напряженности через любую замкнутую поверхность, охватывающую заряды q₁, q₂,…,q_N:

,

где - алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности; N -число зарядов.

1.11. Cвязь между напряженностью и потенциалом:

или -grad j,

где - единичные векторы координатных осей x,y,z.

Знак минус показывает,что вектор направлен в сторону убывания потенциала.

В случае электрического поля, обладающего сферической симметрией, эта связь выражается:

; .

 

В случае однородного поля:

; ,

где Dj=(j₁- j₂) - разность потенциалов двух точек поля вдоль силовой линии; d -расстояние между этими точками.

 

1.12. Принцип суперпозиции (наложения) электрических полей:

; ,

где - напряженность результирующего поля, созданного несколькими точечными зарядами, равная векторной сумме напряженностей складываемых полей;

j - потенциал поля, созданного системой N точечных зарядов, равный алгебраической сумме потенциалов, создаваемых отдельными точечными зарядами.

 

1.13. Работа, совершаемая электрическим полем при перемещении точечного заряда q из одной точки поля, имеющей потенциал j₁, в другую, имеющую потенциал j₂:

.

1.14. Энергия взаимодействия системы точечных зарядов:

,

где j _i - потенциал, создаваемый в той точке, в которой находится заряд q_i, всеми зарядами, кроме i -го.

 

1.15. Электроемкость конденсатора:

,

где q - заряд, накопленный на конденсаторе, - разность потенциалов между обкладками.

 

1.16. Электроемкость уединенной проводящей сферы радиусом R, находящейся в бесконечной среде с диэлектрической проницаемостью e:

,

где S - площадь пластин; d - расстояние между пластинами; e - диэлектричес-кая проницаемость диэлектрика, заполняющего пространство между пластинами.

 

1.17. Соединение конденсаторов в батареи.

 

Соединение	Параллельное	Последовательное
Схема
Сохраняющаяся величена	U1=U2=U3=Un=const	q1=q2=q3=qn=const
Суммируемые величины
Результирующая емкость

 

1.18. Энергия заряженного конденсатора:

,

где q - заряд конденсатора; C- электроемкость; U - разность потенциалов между обкладками.

 

1.19. Пондеромоторная сила - сила, с которой пластины конденсатора притягивают друг друга:

,

где знак минус указывает, что сила F - сила притяжения.

1.20. Объемная плотность энергии:

.

В случае однородного поля, то есть поля, напряженность которого в каждой точке его одинакова как по модулю, так и по направлению ():

.

Для электрического поля в среде с диэлектрической проницаемостью e плотность энергии через напряженность поля Е:

.

1.21. Полная энергия электрического поля через объемную плотность энергии:

.

Примеры решения задач

Пример 1.

Рис. 2

Три точечных заряда q ₁ =q ₂ =q ₃=1нКл расположены в вершинах равно-стороннего треугольника. Какой заряд q₄ нужно поместить в центре треугольника, чтобы указанная система зарядов находилась в равновесии?

 

Дано: q ₁ =q ₂ =q ₃=1 нКл=10^-9 Кл

Найти: q ₄.

Решение.

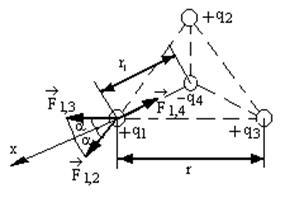
Все три заряда, расположенные по вершинам треугольника, находятся в одинаковых условиях. Поэтому достаточно выяснить, какой заряд следует поместить в центре треугольника, чтобы какой – нибудь один из трех зарядов, например q ₁, находился в равновесии.

Заряд q ₁ будет находиться в равновесии, если векторная сумма действующих на него сил равна нулю (рис. 2):

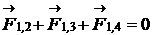, (1)

где , , -силы, с которыми действуют на заряд q ₁ заряды q ₂, q ₃, q ₄.

Заменим векторное равенство (1) скалярным соотношением в проекции на ось x. Учитывая расположение зарядов, выберем ось x, проходящую через заряды q ₁ и q ₄, то есть совпадающую с биссектрисой угла равностороннего треугольника:

.

Учитывая, что F _1,2= F _1,3, получим:

.

Применяя закон Кулона и имея в виду, что q ₁= q ₂= q ₃, получим:

 

или

.

Выполнив преобразования, найдем

. (2)

Из геометрических построений в равностороннем треугольнике следует:

.

C учетом этого формула (2) примет вид:

.

Подставив численные значения, получим

q₄ = -577 пКл.

Следует отметить, что равновесие системы зарядов будет неустойчивым.

Пример 2.

Электрическое поле создано двумя точечными зарядами q ₁=30 нКл и q ₂= -10 нКл. Расстояние между двумя зарядами d =20 см. Определить напряженность электрического поля в точке, находящейся на расстоянии r ₁=15 см от первого заряда, на расстоянии r ₂=10 см от второго заряда (рис.3).

 

Дано: q ₁=30 нКл =30×10^-9 Кл, q ₂=-10 нКл =-10×10^-9 Кл, d =20 см =20×10^{-2 м,} r ₁=15 см =15×10^{-2 м,} r ₂=10 см =10×10^{-2 м.}

Найти: Е.

Решение.

Согласно принципу суперпозиции электрических полей каждый заряд создает поле независимо от присутствия в пространстве других зарядов. Поэтому напряженность электрического поля в искомой точке может быть найдена как векторная сумма напряженностей и полей, создаваемых каждым зарядом в отдельности:

.

Напряженность электрического поля, создаваемого в вакууме (e=1) первым зарядом q ₁:

,

вторым зарядом q ₂:

.

Вектор (рис.3) направлен по силовой линии от заряда q ₁, так как заряд q ₁ положителен; вектор направлен так же по силовой линии, но к заряду q ₂, так как заряд q ₂ отрицателен.

Абсолютное значение вектора найдем, используя теорему косинусов:

 

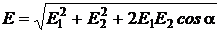, (3)

где a - угол между векторами и может быть найден из треугольника со сторонами r₁, r₂ и d,

.

Производя подстановку в уравнение (3) и вынося общий множитель за знак корня, получим:

.

Подставив численные значения, получим:

Пример 3.

Тонкое кольцо радиусом R =8 см несет заряд, равномерно распределенный с линейной плотностью t=10^-8 Кл/м. Какова напряженность электричес-кого поля в точке, равноудаленной от всех точек кольца на расстояние r =10 см?

 

Дано: R =8 см =8×10^{-2 м,} t=10^-8 Кл/м, r =10 см =10×10^{-2 м.}

Найти E.

Решение.

Рис. 4

Поле создано зарядом, распределенным по тонко-му кольцу заданного ради-уса. Оно не обладает дос-таточной симметрией даже при равномерном распре-делении заряда (нельзя указать точную конфигу-рацию силовых линий), поэтому для расчета на-пряженности можно ис-пользовать только прин-цип суперпозиции .

Разобьем кольцо на элемен-тарные участки d l (рис.4,а).

Каждый такой участок можно принять за точечный заряд, несущий заряд dq =t dl. Элементарный заряд dq, находящийся на элементе dl, создает в данной точке С на расстоянии r вектор напряженности , равный по модулю:

,

где r - расстояние от элемента заряда dq до точки поля С.

Векторы 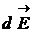от всех элементарных участков образуют симметричный конический веер (рис.4,б). Из соображений симметрии можно заключить, что результирующий вектор направлен вдоль оси кольца. Каждый из составляющих векторов 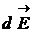вносит в результирующий вектор вклад , равный по модулю:

dЕ₁=dЕcos j

или

, (4)

при этом составляющие , параллельные плоскости кольца, в сумме дают нуль. Проинтегрировав по всему кольцу уравнение (4) и заменив cosj через r и R (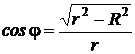), получим абсолютное значение результирующего вектора :

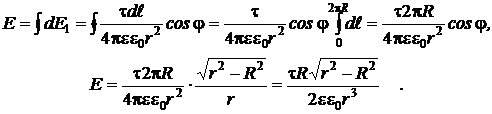
Подставив численные значения, получим:

.

Пример 4.

Точечный заряд Q =-2×10^-10 Кл расположен на продолжении оси диполя, электрический момент которого P_q =1,5×10^-10 Кл×м, на расстоя-нии r =10 см от центра (ближе к положи-тельному заряду диполя). Какую работу надо совершить, чтобы перенести этот заряд в симметрично расположенную точку по другую сторону диполя? Плечо диполя l<<r (рис. 5).

Дано: Q =-2×10^-10 Кл, Р_q =1,5×10^-10 Кл×м, r =10 см =10×10^{-2 м,} l<<r.

Найти: А.

Решение.

Работа А ^*, совершаемая внешними силами при перемещении заряда в электрическом поле, равна работе сил поля, взятой с обратным знаком:

, (5)

где j₁, j₂ – потенциалы соответственно начальной и конечной точек.

Поле создается двумя точечными зарядами +q и –q диполя, и потенциалы точек 1 и 2 следует искать методом суперпозиции. Как видно из рисунка 5, точка 1 находиться на расстоянии от положительного заряда и на расстоянии от отрицательного заряда. В соответствии с этим потенциал первой точки:

 

, (6)

где , – потенциалы в первой точке, созданные соответственно положительным и отрицательным зарядами:

Аналогично потенциал второй точки:

. (7)

Приведем к общему знаменателю каждое из выражений (6) и (7):

(8)

. (9)

Если учесть, что ql=P_q и при r >> l членами можно пренебречь, то выражения (8) и (9) примут вид:

Подставив эти выражения в уравнении (5), получим:

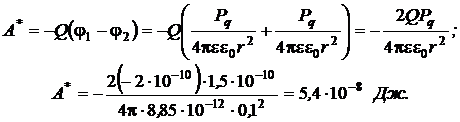
Пример 5

Электрическое поле создано длинным цилиндром радиусом R =1 см, равномерно заряженным с линейной плотностью t=20 нКл./м. Определить разность потенциалов двух точек этого поля, находящихся на расстоянии а₁ =0,5 см и а₂ =2 см от поверхности цилиндра в средней его части (рис. 6).

 

Дано: R =1 см =10^{-2 м,} t=20 нКл/м =20×10^-9 Кл/м, а₁ =0,5 см =5×10^{-3 м, а} ₂ =2 см =2×10^{-2 м.}

Найти: Dj.

Решение.

Для определения разности потенциалов воспользуемся соотношением между напряженностью поля и изменением потенциала:

- qrad j.

Для поля с осевой симметрией, каким является поле цилиндра, это соотно-шение можно записать в виде:

или .

Проинтегрировав это выражение, найдем разность потенциалов двух точек, отстоящих на расстояниях r ₁ и r ₂ от оси цилиндра:

или . (10)

Так как цилиндр и точки взяты вблизи его средней части, то для выражения напряженности поля можно воспользоваться формулой напряженности поля, созданного бесконечно длинным цилиндром:

.

Произведя подстановку в уравнение (10), получим:

или

. (11)

Так как величины r₁ и r₂ входят в формулу (11) в виде отношения, то их можно выразить в любых, но только одинаковых единицах:

r₁=R+a₁ =1,5 см; r₂=R+a₂ =3 см

Подставим численные значения в формулу 11, получим:

 

2. Электрический ток

 

2.1 Сила тока есть скалярная физическая величена, определяемая зарядом, проходящем через поперечное сечение проводника в единицу времени:

.

2.2. Постоянный ток – ток, сила тока и направление которого не изменяется со временем:

,

где q – заряд, прошедший через поперечное сечение проводника за время t.

 

2.3. Плотность тока есть величина, определяемая силой тока, проходящего через единицу площади поперечного сечения проводника, перпендикулярного направлению тока:

.

2.4. Сопротивление однородного проводника:

,

где r_э - удельное сопротивление вещества проводника; - его длина; S- площадь поперечного сечения.

2.5. Закон Ома

· для неоднородного участка цепи:

 

,

 

· для однородного участка цепи ( =0):

 

,

· для замкнутой цепи:

,

где - разность потенциалов на концах участка цепи; 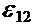- ЭДС источников тока, входящих в участок; U ₁₂ - падение напряжения на участке цепи; R ₁₂ - сопротивление участка цепи; R - сопротивление внешней цепи; r - внутреннее сопротивление источника тока; - ЭДС всех источников тока цепи.

 

2.6. Работа постоянного тока на участке за время t:

A=IUt.

2.7. Мощность тока P_R при прохождении тока по участку с сопротивлением R:

.

2.8. Полная мощность цепи - мощность, развиваемая источником тока:

 

.

 

2.9. Коэффициент полезного действия источника тока:

 

.

 

2.10. Закон Джоуля - Ленца. Если ток проходит по неподвижному проводнику, то вся работа идет на его нагревание и количество теплоты, выделяющееся в участке цепи за время dt:

 

.

 

В случае постоянного тока (I =const):

 

.

 

2.11. Законы Кирхгофа.

Первый закон Кирхгофа: алгебраическая сумма токов, сходящихся в узле, равна нулю; т. е.

,

где n – число токов, сходящихся в узле.

 

Второй закон Кирхгофа: в любом замкнутом контуре разветвленной цепи алгебраическая сумма произведений сил токов I_i на сопротивление R_i соответствующих участков этого контура равна алгебраической сумме ЭДС , встречающихся в этом контуре; т. е.

где n - число участков, содержащих активное сопротивление; к - число источников в контуре.

При решении задач по законам Кирхгофа надо придерживаться следующих правил.

1. Обозначить на схеме буквами узлы и контуры.

2. Произвольно выбрать направление токов (если они не оговорены условием задачи) во всех участках цепи и обозначить их на чертеже стрелками.

3. Учесть направление токов при составлении первого закона. Положи-тельными считать токи, подходящие к узлу, а отрицательными – отходя-щие от узла.

4. Составить систему уравнений для первого закона Кирхгофа. Число уравнений, составленных по этому закону, должно быть на единицу меньше числа узлов в цепи.

5. Выбрать произвольно направление обхода контуров. Условиться, что ЭДС в уравнении будет положи-тельной, если направление от отрицательного полюса к положительному совпадает с направлением обхода, в противном случае ЭДС следует считать отрицательной.

6. Считать падение напряжения в цепи (IR) положи-тельным, если выбранное ранее направление тока на этом участке (между двумя узлами) совпадает с направлением обхода контура, и отрица-тельным, если направление тока не совпадает с направлением обхода контура.

7. Первый контур выбрать произвольно. При составлении уравнений следующих контуров надо включать в них контуры, ранее не входящие.

8. Число уравнений, составленных по второму закону Кирхгофа, определяется следующими условиями. Если число контуров в цепи m, а узлов в ней n, то число независимых уравнений, достаточных для решения, будет равно m-n +1.

9. Получение в ответе токов с отрицательными знаками означает, что было выбрано направление, обратное действительному.

Пример 6

Найти токи, протекающие в каждой ветви электрической цепи (рис. 7), если , R₁ =0,5 Ом, R₂ =0,3 Ом, R₃ =120 Ом. Внутреннее сопротивление источника тока не учитывать.

 

Дано: , , R₁ =0,5 Ом, R₂ =0,3 Ом, R₃ =120 Ом.

Найти: I ₁, I ₂, I ₃.

Решение.

Задача дана для расчета разветвленных цепей, когда в них есть несколько источников тока. При решении задач такого типа рационально пользоваться законами Кирхгофа.

1. Обозначаем на схеме (рис. 7) контуры, узлы и направление токов.

2. Устанавливаем число ветвей m (в данной схеме их три) и число узлов n (в данной схеме их два - в точках В и Н).

3.

Рис. 7

Для составления уравнений по первому закону Кирхгофа достаточно выбрать один из указанных узлов. Выберем узел В, в котором сходятся токи от трех проводников. Учитывая направления токов, получим:

I ₁ -I ₂ -I ₃=0. (12)

4. Устанавливаем число уравнений, необходимых для решения задач по второму закону Кирхгофа. Это число уравнений равно m-n +I=3-2+I=2. Выбираем контуры ВСДНВ и АВНТА.

5. Устанавливаем обход по контуру ВСДНВ, учитывая правило знаков при обходе тока внутри источников ЭДС. Выбираем обход по часовой стрелке, при котором ЭДС будет положительной. С учетом выбранного ранее направления токов составляем первое уравнение по второму закону Кирхгофа:

(13)

Cоставляем уравнение для второго контура BHTAB. Так как в этом контуре два источника тока ( > ), обход начинаем от к по часовой стрелке.

Кроме того, знаки при ЭДС и падения напряжения IR устанавливаем в соответствии с ранее приведенными правилами:

(14)

Подставив в равенства (12), (13), (14) значения сопротивлений и ЭДС, получим систему уравнений:

Эту систему уравнений с тремя неизвестными можно решить обычными приемами алгебры, в данной задаче удобно воспользоваться методом определителей (детерминантов). С этой целью перепишем уравнения еще раз в следующем виде:

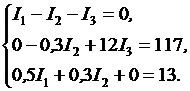
Искомые значения токов найдем из выражений:

; ; ,

где D - определитель системы уравнен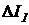ий; , , - определители, полученные заменой соответствующих столбцов определителя D столбцами, составленными из свободных членов трех вышеприведенных уравнений.

Составим и вычислим определитель системы и определители для I₁, I₂, I₃:

; ;

; .

Отсюда получаем:

;

;

.

 

Магнитное поле тока

 

3.1 Характеристики магнитного поля:

- вектор магнитной индукции – характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками;

- вектор напряженности – характеризует магнитное поле, создаваемое только макротоками.

В случае однородной изотропной среды:

= ,

где - магнитная проницаемость среды; - магнитная постоянная, =4p×10^-7Гн/м.

3.2 Закон Био-Савара-Лапласа. Элемент проводника с током I создает в некоторой точке А индукцию поля:

; ,

 

где - - радиус-вектор, проведенный из элемента проводника в точку А; a – угол между радиусом-вектором и направлением тока в элементе проводника (рис. 8).

3.3 Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током:

,

где 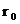- кратчайшее расстояние от оси проводника до точки, в которой определяется магнитная индукция.

Вектор индукции направлен по касательной к силовой линии. Для бесконечно длинного проводника силовыми линиями являются окружности. Направление силовой линии (а значит, и направление вектора ) определяется по правилу правого винта (рис. 9).

3.4 Магнитная индукция поля, создаваемого отрезком проводника с током: