Неопределенный интеграл.

Перед изучением темы необходимо убедится в твердом знании таблицы производных основных элементарных функций.

Сначала вводится понятие первообразной данной функции. Функция называется первообразной данной функции на заданном промежутке, если выполняется равенство в любой точке этого промежутка.

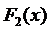Любые две первообразных и данной функции отличаются друг от друга на произвольную постоянную величину: .

Совокупность первообразных данной функции называется ее неопределенным интегралом и обозначается так:

, где

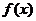- под интегральная функция,

- под интегральное выражение,

x – переменная интегрирования.

Таким образом, интегрирование – это отыскание совокупности первообразных функции по заданной ее производной.

Основные свойства неопределенного интеграла:

6 Неопределенный интеграл не зависит от обозначения переменной интегрирования.

Таблица основных неопределенных интегралов:

Приступая к интегрированию убедитесь в безупречном знании таблицы основных интегралов.

Определенный интеграл

Пусть функция y=f(x) определена и непрерывна на некотором отрезке [a,b]. Если F(x)+c – первообразная функции для f(x), то приращения F(b)-F(a) первообразных функций при изменении аргумента x от x=a до x=b называется определенным интегралом и обозначается символом , т.е.

Для вычисления определенного интеграла от данной функции f(x) на отрезке [a;b] служит формула Ньютона-Лейбница, связывающая определенный интеграл с неопределенным через первообразную:

Задача 11. Найдите интегралы:

Решение.

1. Пользуясь свойствами неопределенного интеграла, запишем его так, чтобы получить табличные интегралы:

2. Этот интеграл можно привести к табличному, если воспользоваться заменой переменной (подстановка). Пусть 5-x3=t. Находим дифференциалы обеих частей подстановки: d(5-x³)=d t, или -3x²d x =d t, откуда .

Данный в условии интеграл примет вид

Здесь на втором шаге введена замена переменной t вместо x, в результате полечен табличный интеграл, а потом сделан возврат к прежней переменной x.

Вычислить определенный интеграл

Решение. Этот интеграл можно вычислить, введя следующую замену переменной: 9-5sin x= t.

Тогда d(9-5sinx)=d t

или –5 cos x d x =d t

откуда. Cos x d x = - 1/5 d t

При замене переменной в определенном интеграле поменяются и границы интегрирования. Новые границы интегрирования найдем из подстановки, то есть из равенства 9-5sin x= t, полагая в нем x=0, а затем. Соответственно получим . получим t=9 и t=4. Это можно записать короче так: .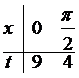

Итак.

Задача 13.

Сделайте чертеж и вычислите площадь фигуры, ограниченной линиями y=8+2x-x² и y+2x-4.

Решение. Первая из двух данных линий – парабола, направленная ветвями вниз, поскольку коэффициент при x² отрицательный, а вторая линия – прямая, пересекающая обе оси координат.

Для построения параболы найдем координаты ее вершины: y’=2-2x; 2-2x=0, x=1 – абсцисса вершины; y(1)=8+2∙1-1²=9 – ее ордината, N(1;9) - вершина. Теперь найдем точки пересечения параболы и прямой, решив систему уравнений

Приравнивая правые части уравнения, левые части которых равны, получим 8+2x-x²=2x-4 или x²-12=0, откуда .

Итак, точки - точки пересечения параболы и прямой (рис. **).

Построим прямую y=2x-4. Она проходит через точки (0;-4),(2;0) на осях координат. Для построения параболы можно еще ее точки пересечения с осью 0x, то есть корни уравнения 8+2x-x²=0 или x²-2x-8=0. По теореме Виета легко найти его корни: x₁=2, x₂=4. На рис.4 изображена фигура (параболический сегмент M₁N M₂), ограниченный данными линиями.

Вторая часть задачи состоит в нахождении площади этой фигуры. Ее площадь можно найти с помощью определенного интеграла по формуле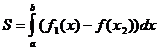

Применительно к данному условию, получим интеграл

Ответ: (кв. ед.)

Задача 14.

Сделайте чертеж и вычислите объем тела, образованного вращением вокруг оси O y фигуры, ограниченной линиями x y =3, y=1, y-3=0.

Решение. Чтобы сделать чертеж, запишем уравнение первой линии, в виде 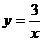- это функция обратно пропорциональной зависимости, а ее график – гипербола, две ветви которой расположены в первой и третьей координатных плоскостях. Две другие линии – это прямые, параллельные оси Ox (рис.4). Найдем точки пересечения гиперболы с прямыми. Если в уравнении 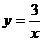положим y=1, то получим x=3, а если положим y=3, то получим x=1. Итак, A(1;3), B(3;1) – точки пересечения данных линий. Теперь вычислим объем тела, которое получится в результате вращения заштрихованной фигуры вокруг оси O y. Это можно сделать, пользуясь формулой , где x=φ(y).

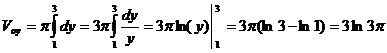В условиях данной задачи x y =3, откуда , c=1, d=3, таким образом (куб. ед.)

Ответ: V=3l n3π (куб. ед.)

Задача 15.

Точка движется прямолинейно с ускорением (м/с²) a(t)=5t²-7t+2. Найдите уравнение скорости V(t), если V(0)=4м/с.

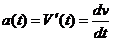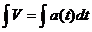Решение. Поскольку ускорение есть производная скорости, то чтобы найти скорость по ее производной, надо найти интеграл от ускорения в самом деле, так как , то d v=a(t)d t и тогда, интегрируя обе части последнего равенства и учитывая, что , получим или

С учетом того, что V(0)=4, получим, полагая t=0, что C=4. Значит, скорость движения точки в условиях данной задачи выражается уравнением

Ответ: