Задача 16.
Решите дифференциальное уравнение 
Решение. Это уравнение первого порядка с разделяющимися переменными. Для разделения переменных этого уравнения в виде 
и разделим его по членно на произведение 
. В результате получим 
или
Интегрируя обе части последнего уравнения, получим общее решение
аrc sin y =arc sin x + C.
Найдем теперь частное решение, удовлетворяющее начальным условиям 
. Подставляя в общее решение начальные условия, получим
; откуда C=0.
Следовательно, частное решение имеет вид arc sin y=arc sin x, но синусы равных дуг равны между собой
sin (arc sin y)=sin (arc sin x).
Откуда, по определению арксинуса, следует, что y=x
Ответ: y =x
Задача 17.
Решите дифференциальное уравнение y’’=sin2x при начальных условиях:
Решение. Запишем уравнение так 
. Интегрируя обе части, получим 
откуда 
Интегрируя левую и правую части уравнения еще раз, найдем общее решение 
, (**). Чтобы найти частное решение, удовлетворяющее начальным условиям, подставим начальные условия в выражения (*) и (**), для первой производной и функции с тем, чтобы получить систему уравнений с неизвестными С1 и С2. В результате получим систему 
, решая которую находим, что C1=1, С2=0. Тогда частное решение уравнения такое 
Ответ: 
Задача 18.
Составить уравнение кривой, проходящей через точку 
и имеющей угловой коэффициент 
в любой точке касания.
Решение. По заданной производной , рассмотрим её как дифференциальное уравнение, найдем функцию, удовлетворяющую этому уравнению, то есть общее решение. Имеем 
или y d y =d x. Интегрируя обе части, последнего уравнения находим 
или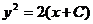 
- общее деление это множество кривых, удовлетворяющих условию . Найдем среди них ту, которая проходит через точку , то есть координаты точки A должны удовлетворять уравнению кривой. Подставляя эти координаты в общее решение, получим 
, откуда С =0. Таким образом, искомое уравнение кривой, удовлетворяющей условий задачи, 
.
Ответ: .
Теория вероятностей.
Испытанием называется выполнение совокупности некоторых условий.
Событие – это результат испытания. События могут быть трех видов: достоверные, невозможные, случайные. Среди случайных событий различают не совместн ые и совместные, независимые и зависимые. Противоположными называют два единственно возможных несовместных события.
Классическое определение вероятности: вероятностью события А называется отношение числа m исходов, благоприятствующих наступлению события А, к числу n исходов как благоприятствующих так и не благоприятствующих наступлению события А.
Обозначение 
. По определению, 0<P(A)<1.
Вводится понятие суммы событий (несовместных, совместных), произведения событий (независимых, зависимых), формулируются теоремы вероятности суммы, произведения событий, вероятности хотя бы одного из независимых событий, полной вероятности. Эти понятия и теоремы надо повторить по учебнику.
Кроме классического определения вероятности используется статическое определение, согласно которому вероятностью события (относительной частотой или частностью) называется отношение числа M исходов, благоприятствующих наступлению события A к числу N фактически произведенных испытаний.
Обозначение: 
.
Практика показывает, что P(A)≈W(A).Поэтому при решении задач часто используют систематическую вероятность.
Задача 19.
В партии 100 деталей, из них 1 нестандартных. Определить вероятность того, что взятая наудачу деталь окажется стандартной?
Решение. Пусть события A означают, что наудачу взятая деталь стандартная. Число стандартных деталей m=100-12=88. Число всех деталей в партии n=100. По определению, 
Ответ: P(A)=0,88.
Задача 20.
В коробке перемешаны 20 синих и 15 белых шаров одинакового размера. Наудачу вынимается один шар. Какова вероятность того, что вынутый шар – белый?
Решение. m=15 – число белых шаров, n=20+15=35 – число всех шаров, белых и небелых. Пусть Б – вынут белый шар. Тогда 
Ответ: 
Задача 21.
В урне 8 красных и 5 синих шаров. Из урны наугад вынимаются по 2 шара. Найти вероятность того, что они разного цвета (событие А).
Решение. Число благоприятных исходов m=8·5=40, так как каждый красный шар, а их8, может быть, случайно вынут с каждым из 5 синих шаров. Число же любых пар наудачу вынутых шаров равно числу сочетаний из 13 по 2, то есть 
. 
Ответ: 
Задача 22.
Карточка “Спортлото” содержит 36 чисел. В тираже участвуют 5 чисел. Какова вероятность того, что верно будут угаданы все 5 чисел (событие А)?
Решение. Число сочетаний по 5 чисел, отличающихся составом, из 36 равно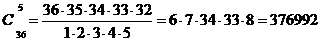 
. Только одно из этих сочетаний приемлемо. То есть искомая вероятность 
Ответ:
Задача 23.
В лотерее из 12 билетов 8 выигрышных. Какова вероятность того, что из 6 наудачу выбранных билетов а) 2 выигрышных? Б) 3 выигрышных?
Решение. Пусть А – наудачу взятый билет – выигрышный, 
– не выигрышный.
По условию, 
. Требуется найти вероятность того, что из 6 взятых билетов а) равно 2 выигрышных, б) равно 3 выигрышных. Задача решается с помощью формулы Бернулли: P n (K)=CK pK qn-k. В данной задаче n=6 – число независимых испытаний, k=2, k=3 – число появлений события А.
Получим 
Задача 24.
Высеиваются три семени A,B,C. Вероятность всхожести для каждого из них такова: P(A)=0.6; P(B)=0.7; P(C)=0.5. Какова вероятность того, что взойдет хотя бы одно из семян?
Решение. Известно, что вероятность появления хотя бы одного из n независимых событий (E) вычисляется по формуле P(E)=1-q1q2...q n, где
q1,q2,...,q n – вероятности противоположных событий:
(q1=1-p1).
В данной задаче по условию p1=0,6 тогда q1=1-0,6=0,4
p2=0,7 q2=0,3
p3=0,5 q3=0,5
Таким образом P(E)=1-0,4·0,3·0,5=1-0,06=0,94.
Ответ: P(E)=0,94=94%.
Задача 25.
Десять различных книг расставляются наугад на одной полке. Какова вероятность того, что три определенные книги окажутся поставленными рядом?
Решение. Найдем число из 10 элементов по 3, то есть число троек, отличающихся составом, из десяти книг:
Только одна из этих 120 троек удовлетворяет условию задачи.
Значит 
Ответ:
ЛИТЕРАТУРА
Основная
Математика для техникумов. Алгебра и начало анализа / Под ред. Г.Н. Яковлева. 4.1 – М.: Наука. 1987
Математика для техникумов. Алгебра и начало анализа / Под ред. Г.Н. Яковлева. 4.2 – М.: Наука. 1988
Математика для техникумов. Геометрия / Под ред. Г.Н. Яковлева. - М.: Наука. 1989
Федин Н.Г., Федин С.Н. Геометрия. – М.: Высшая школа. 1989
Апанасов П.Г., Орлов М.И, Сборник задач по математике. – М.: Высшая школа. 1987
Дополнительная
Афансьев О.Н., Бродский Я.С., Павлов А.Л. Математика для техникумов. – М.: Наука. 1991
Афансьев О.Н., Бродский Я.С., Гуткин И.И., Павлов А.Л. Сборник задач по математике на базе средней школы. – М.: Наука. 1992
Богомолов Н.В. Практические задачи по математике. –М.: Высшая школа. 1990
Валуцэ И.И., Дилигул Т.Д. Математика для техникумов на базе средней школы. – М.: Наука. 1989
Цыпкин А.Г. Справочник по математике для средней школы /Под ред. С.А. Степанова. – М.: Наука. 1979
Сергиенко Л.Ю., Самойленко П.И. Планирование учебного процесса по математике. –М.: Высшая школа. 1987
Калинина В.Н., Панкин В.ф. Математическая статистика. – М.: Высшая школа. 1994
Методические рекомендации по математике. – М.: Высшая школа. 1976. вып.1; 1978, вып. 2; 1980, вып.3; 1981, вып.4; 1982, вып.5; 1984, вып.6; 1985, вып.7; 1986, вып.8; 1987, вып.9; 1988, вып.10; 1989, вып.11; 1990, вып.12.