Применение производной в задачах с параметром

При решении задач с параметром часто бывает необходимо строить график некоторой функции. В простейших случаях (квадратичная, дробно-линейная функции) можно обойтись без производной, но более сложные графики строим с применением производной. При построении графиков функций будем пользоваться сокращенной схемой исследования, состоящей из трех пунктов: 1) нахождение области определения; 2) определение нулей функции и промежутков знакопостоянства; 3) нахождение экстремумов и промежутков монотонности.

1. Определить число решений уравнения в зависимости от параметра. Решение. Строим график функции . Для этого находим производную . Приравниваем ее к нулю, чтобы найти точки экстремумов и промежутки монотонности (возрастания и убывания). Уравнение имеет корни . Составим таблицу монотонности.

 

	+		–		+
				–2

 

Отметим, что функция обращается в ноль в точках 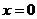, . Эти данные позволяют построить схему графика (на рисунке представлен более точный график, построенный с использованием второй производной, но для решения данной задачи такая точность не обязательна). Мысленно двигая горизонтальную прямую , считаем число точек пересечения с графиком. Получаем при одно решение, при два решения, при три решения. Ответ: при одно решение, при два решения, при три решения.

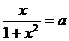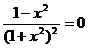2. Построить график функции . Определить, при каких значениях параметра уравнение имеет хотя бы один корень в промежутке . Решение. Находим производную = . Приравниваем ее к нулю, чтобы найти точки экстремумов и промежутки монотонности: , . Составим таблицу монотонности.

 

 

	–		+		–
		–0,5		0,5

 

Отметим, что функция обращается в ноль в точке 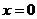, при положительна, а при отрицательна. Эта функция имеет также важную особенность: при неограниченном увеличении 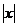значения функции стремятся к нулю, так как знаменатель содержит в более высокой степени, чем числитель. Эту особенность надо отразить на чертеже, «устремляя» график к оси абсцисс при удалении «на бесконечность». Теперь выделим часть графика, соответствующую (рис. 3). Для этого найдем значения , . По чертежу видно, что уравнение 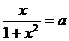имеет решение, принадлежащее промежутку , в том случае, когда . Ответ: .

3. Построить график функции . Определить, при каких значениях параметра уравнение имеет два различных корня в промежутке . Решение. Область определения . Находим производную . Приравниваем ее к нулю, чтобы найти точки экстремумов и промежутки монотонности: . В таблицу монотонности необходимо внести колонку для той точки, в которой производная не существует, т. е. 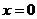. Получаем график на рис. 4.

 

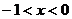
	+		–	Не сущ.	–		+
		–2		Не сущ.

Теперь выделим часть графика, соответствующую (рис. 5). Для этого найдем значения . По чертежу видно, что уравнение имеет два различных решения, принадлежащих промежутку , в том случае, когда . Ответ: .

 

4. При каких значениях параметра уравнение имеет хотя бы один корень? Решение. Преобразуем уравнение к виду 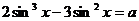, . Положим и построим график функции 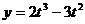с областью определения . Находим производную . Приравниваем ее к нулю, чтобы найти точки экстремумов и промежутки монотонности: , . Составим таблицу монотонности:

 

 

	+		–		+
				–1

 

Найдем значение функции в точке : 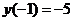. Теперь можем построить график (рис. 6). По графику видно, что уравнение имеет решение, принадлежащее множеству , если 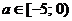. Ответ: .

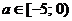5.

При каких значениях уравнение имеет решение? Решение. Применим формулу тройного аргумента: . Получим уравнение . Положим и построим график функции с областью определения . Находим производную . Находим нули производной , и составим таблицу монотонности. Найдем значения функции в точках экстремумов и на концах отрезков: ; ; . Следовательно, множество значений – это отрезок 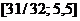. Ответ: .

6. Решить уравнение при условии, что оно имеет ровно два различных корня. Решение. Рассмотрим функцию и построим ее график. Для этого найдем производную . Так как производная обращается в 0 только в точке (при этом ), получаем таблицу монотонности на рис. 7, с учетом которой строим график (рис.8). Получаем, что ровно два корня уравнение имеет при и один из этих корней . Остается найти второй корень уравнения 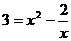. Так как – корень уравнения , то можно выделить сомножитель : . Из уравнения получаем . Ответ: .

7.

При каких значениях параметра уравнение имеет ровно один корень? Решение. Исследование будет немного проще, если ввести замену . Тогда уравнение примет вид 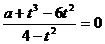. Это уравнение должно иметь ровно один положительный корень. Данное условие равносильно тому, что уравнение имеет ровно один положительный корень, не равный 2 ( не входит в ОДЗ). Изобразим график функции , 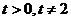(рис. 3). Для этого найдем производную , точки экстремумов и . Точку 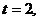надо «выколоть». Проследим, при каких значениях прямая имеет с графиком ровно одну точку пересечения. По графику видно, что это условие выполняется при . Ответ: .

 

8. Найти значение , при котором является точкой максимума функции . Решение. Находим производную . Приравниваем ее к нулю, чтобы найти точки экстремумов и промежутки монотонности: , . В данном случае, очевидно, что — больший корень, причем производная положительна при и при , а между корнями она отрицательна.. Значит, максимум функции находится в точке . Отсюда . Ответ: 7.

9. При каких значениях функция убывает на всей числовой прямой? Решение. Найдем производную . Чтобы функция , непрерывная на всей числовой прямой, являлась всюду убывающей, потребуем, чтобы для всех выполнялось неравенство . Квадратичная функция не меняет знак на всей числовой прямой, если ее дискриминант . Получаем неравенство .

10. При каких значениях параметра функция возрастает на всей числовой прямой? Решение. Найдем производную . Чтобы данная функция являлась всюду возрастающей, потребуем, чтобы для всех выполнялось неравенство . Обозначим и получим неравенство , или, учитывая , , которое обязано выполняться для всех . Решим соответствующее квадратное уравнение и получим корни , . Очевидно, условие выполняется в том и только в том случае, если оба корня не положительны, т. е. , или . Ответ: .

11. *При каких значениях параметра функция возрастает при всех ? Решение. Найдем производную . Чтобы данная функция являлась возрастающей при всех , потребуем, чтобы для всех выполнялось неравенство . Это выполнено при условии , или . Ответ: .

12. При каком функция 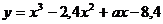не имеет экстремума в критической точке? Решение. Находим производную . Чтобы в критической точке не было экстремума, нужно, чтобы в этой точке производная обращалась в ноль, но не меняла знака. Это возможно, если квадратный трехчлен является полным квадратом, т. е. его дискриминант равен нулю: . Отсюда . Ответ: .

13. При каком функция имеет положительную точку максимума? Решение. Находим производную . Приравниваем ее к нулю . Корни этого уравнения . Судя по распределению знаков , максимум должен быть в точке, соответствующей меньшему корню, в данном случае . Значит, должно выполняться неравенство 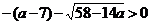. Решаем неравенство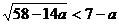 . Ответ: .

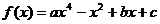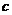14. На рисунке 9 изображен график функции . Определить знаки коэффициентов . Решение. Знаки и определяются легко: , так как точка пересечения с осью Оу лежит выше оси Ох. Так как при 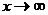, то . Чтобы определить знак , найдем производную: , число – это значение производной в точке 0. Но по углу наклона касательной в точке пересечения с осью ординат (или по тому, что функция в окрестности этой точки убывает) мы можем сделать вывод, что производная в этой точке отрицательна, т. е. . Ответ: 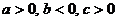.