Здесь рассмотрим основные понятия обработки информации при формировании оценок неизвестных параметров динамических систем по результатам случайных наблюдений. Начнем рассмотрение таких задач с наиболее простой задачи оценивания неизвестных параметров распределения.
Лекция 22. Задачи оценивания как частный случай статистического решения
Многие практически важные задачи сводятся к получению статистических выводов относительно всех или некоторых неизвестных параметров функции распределения, принадлежащие известному семейству функций. Например, пусть имеется случайный вектор Х, вид плотности распределения которого известен, но неизвестны параметры плотности распределения.
- неизвестный параметр (скаляр или вектор)
Проведены измерения и получен вектор 
- ошибка измерений СВ
Требуется по результатам измерений найти оценку вектора неизвестных параметров
Искомая оценка будет являться функцией результатов измерений.
,
где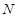 
-число измерений.
Предположим, что в качестве измерений Y рассматривается возможная реализация случайной величины x. Тогда, как известно, в качестве математического ожидания можно взять выборочное математическое ожидание
,
а в качестве дисперсии можно взять исправленную выборочную дисперсию
Если исходное распределение случайной величины Х является нормальным - 
, то есть 
, тогда
О свойствах точечных оценок было сказано выше (см. «Обработка результатов статистического моделирования»). Кратко напомним эти свойства.
1. Несмещенность
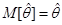
2. Состоятельность
3. Эффективность
Оптимальные оценки
Перечисленные выше свойства точечных оценок характеризуют точность формируемых оценок, при этом с каждой оценкой параметра связана ошибка, и величина этой ошибки может сильно влиять на качество получаемых решений. С целью учёта влияния ошибки на качество получаемых решений вводится понятие оптимальной оценки. Они формируются с использованием понятия функции потерь.
Предположим, что с каждой оценкой 
,полученной по результатам 
наблюдений (опытов) параметра связана функция потерь 
.
В качестве функции потерь обычно используются следующие функции:
1. Квадратичная
Для скалярного параметра 
: 
Для векторного параметра : 
,
где 
- весовая матрица.
2. Простая
3. Модуль ошибки
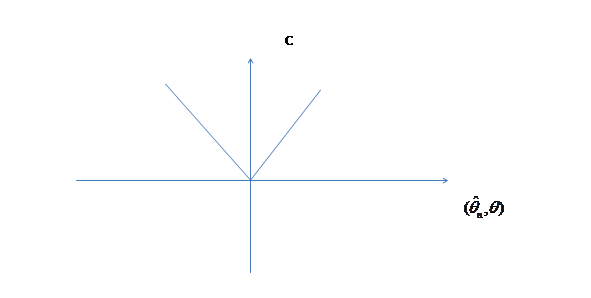
4. Экспоненциальная
5. Прямоугольная
Основные свойства функций потерь
1. Скалярная функция n-переменных.
2. Значение функции потерь в нуле равно нулю (за исключением простой).
3. Неубывающая функция ошибки.
4. Симметричная относительно нуля.
Так как оценка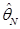 
- случайная величина, то и потери будут также случайной величиной, поэтому для сравнения оценок между собой и выбора наилучшей оценки рассматривают статистические характеристики функции потерь, так называемые функции риска.
Можно строить различные функции риска. Наиболее часто используются следующие:
1. Условный риск – математическое ожидание функции потерь при фиксированном значении параметра
Наиболее предпочтительной оценкой 
в этом случае естественно считать такую оценку, которая минимизирует условный риск для всех значений , однако такие оценки существуют в редких случаях и называются они равномерно наилучшими. Обычно оценка , минимизирующая условный риск зависит от и поэтому не ясно какую из различных оценок при разных выбирать. Эта зависимость исключается, если воспользоваться байесовским подходом, при котором полагается случайной величиной с известным законом распределения.
2. Средний риск – это полное математическое ожидание функции потерь.
Оценка , минимизирующая риск является байесовской
;
- байесовский риск.
3. Апостериорный риск – это апостериорное математическое ожидание функции потерь.
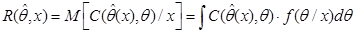
Решения получаемые путём минимизации среднего и апостериорного риска эквивалентны, то есть в том и другом случае получаем байесовскую оценку.
Действительно, из выражения для среднего риска, находим:
Поскольку 
, то минимум среднего риска по достигается в той же точке 
, что и минимум апостериорного риска.
Примеры байесовских оценок
- Байесовская оценка для простой функции потерь
Подставим выражение для функции потерь в выражения для апостериорного риска.
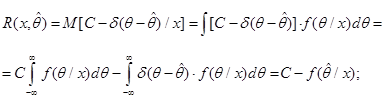
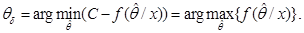
Таким образом, для простой функции потерь байесовская оценка является оптимальной по критерию максимума апостериорной плотности вероятности.
- Байесовская оценка для квадратичной функции потерь
Будем считать, что параметр – скалярный. Тогда функцию потерь можно записать как функцию разности.
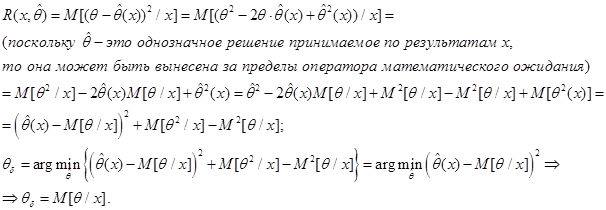
Таким образом для квадратичной функции потерь байесовская оценка представляет собой условное или апостериорное математическое ожидание оцениваемого параметра. При этом эта оценка является оптимальной по критерию минимума средней квадратической ошибки.
Недостатком байесовского оценивания является необходимость знания априорного распределения. Существуют методы оценивания, не использующие предположение об априорном распределения оцениваемого параметра. К таким методам относятся: метод максимального правдоподобия (ММП) и метод наименьших квадратов (МНК).
Метод максимального правдоподобия
Для реализации метода необходимо знать закон распределения результатов наблюдений, связанных с оцениваемым параметром. Применение ММП для оценки параметра 
экспоненциального закона распределения было рассмотрено в разделе III, лекция 15 «Методы получения точечных оценок параметров распределения».
Здесь рассмотрим применение ММП для следующей задачи. Пусть требуется оценить n-мерный вектор 
неизвестных параметров по результатам N измерений. При этом каждое измерение 
- 
представляет собой вектор размерности 
.
,
где 
, 
, 
, 
.
Запишем плотность распределения ошибки измерений.
Функция правдоподобия представляет собой плотность распределения гауссовского вектора с математическим ожиданием 
и ковариационной матрицей 
.
Для нашей задачи функция правдоподобия имеет вид:
Учитывая, что неизвестный вектор 
входит только во второе слагаемое, то максимизация функции правдоподобия с целью нахождения оценки 
, эквивалентна минимизации по квадратичной формы 
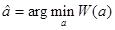
Воспользуемся необходимым условием, для этого вспомним правило дифференцирования квадратичных форм.
Имеем систему из n нелинейных уравнений относительно параметра . Для решения системы можно использовать какой-либо из методов математического программирования.
Для оценок максимального правдоподобия при нормальном законе ошибок измерений выполняется свойство состоятельности.
Метод наименьших квадратов
Метод находит широкое применение в задачах оценки параметров движения КА. Также используется в навигационных системах. Рассмотрим ту же модель, что рассматривали в ММП. Идея метода состоит в том, что в качестве оценок неизвестного параметра принимаются значения параметра, для которого полученные измерения наиболее близкие к значениям, предсказываемым или вычисляемым с помощью модели измерений. В качестве меры близости используется квадратичная форма (поэтому метод называется методом наименьших квадратов - МНК). Для применения МНК необходимо, чтобы ошибки измерений были центрированы (математическое ожидание равно нулю).
В качестве меры близости измеренных значений 
и предсказанных моделью значений 
, примем квадрат их разности (или квадрат разности ошибки, а в векторном случае квадратичную форму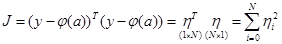 
).
Мы получили систему из n уравнений, которая практически совпадает с системой уравнений для ММП при 
. Отсюда следует, что при аддитивных и независимых ошибках измерений, распределенных по нормальному закону, МНК можно рассматривать как частный случай ММП.
Метод наименьших квадратов в приведённом виде использует всю выборку и не требует никаких априорных статистических сведений о динамической системе и ошибках измерений, кроме предположений о центрированности ошибок, то есть равенстве нулю их математического ожидания. Недостатком этой схемы МНК является сложность системы уравнений, приводящая к неоднозначности решений, а так же необходимость запоминания больших массивов информации и обработки этих массивов в реальном масштабе времени. Для снижения количества запоминаемой информации разработана рекуррентная схема применения метода наименьших квадратов, в которой каждое текущее измерение обрабатывается, и формируется текущая оценка неизвестного параметра на основе всех предыдущих и текущего измерений. Поэтому здесь в каждый конкретный момент времени нужно помнить только последний момент измерений.
Рассмотрим использование МНК для линейной модели измерений.
В качестве невязки или меры расхождения примем следующую квадратичную форму:
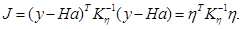
Необходимые условия минимума квадратичной формы:
|
- система нормальных уравнений,
где 
- оценка параметра 
.
Найдём выражение для оценки из системы нормальных уравнений:
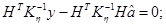
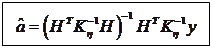
В данном случае необходимые условия совпадают с достаточными условиями.
Найдём точность полученной оценки, которую будем характеризовать ковариационной матрицей ошибок оценок. Для этого перепишем соотношения для измерений в таком виде: 
и умножим его слева на 
. В результате получим:
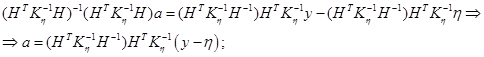
Запишем выражение для ошибки оценки
Найдём выражение для ковариационной матрицы ошибок оценок:
Таким образом, ковариационная матрица ошибок оценок определяется следующим соотношением:
|
Литература
1. Статистическая динамика и оптимизация управления летательных аппаратов: Учебн. пособие для авиационных специальностей вузов/ А, А. Лебедев, В. Т. Бобронников, М. Н. Красильщиков, В. В. Малышев. – М. Машиностроение, 1985.
2. Статистическая динамика и оптимизация управления летательных аппаратов: Учебн. пособие для вузов/ В. Т. Бобронников и др.; под общ. ред. М. Н. Красильщикова, В. В. Малышева. – Изд. 2-е, перераб. и доп. – Москва: Альянс, 2013.
3. Росин М. Ф., Булыгин В. С. Статистическая динамика и теория эффективности систем управления: Учебник для вузов. – М.: Машиностроение, 1981.
4. Тихонов В. И., Харисов В. Н. Статистический анализ и синтез радиотехнических устройств и систем: Учеб. пособие для вузов. – М.: Радио и связь, 2004.