Тройные интегралы
П.1. Понятие тройного интеграла. Свойства тройного интеграла
Пусть функция  непрерывна в замкнутой области
непрерывна в замкнутой области  (т.е. в области V пространства Оxyz). Разобьем область V сеткой произвольных гладких поверхностей на n элементарных областей
(т.е. в области V пространства Оxyz). Разобьем область V сеткой произвольных гладких поверхностей на n элементарных областей  (
( ), объемы которых обозначим
), объемы которых обозначим  . В каждой элементарной области выберем произвольным образом точку
. В каждой элементарной области выберем произвольным образом точку  (
( ), умножим значение
), умножим значение  функции в этой точке на
функции в этой точке на  и составим сумму всех таких произведений
и составим сумму всех таких произведений
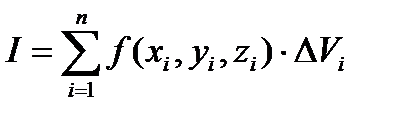 (1)
(1)
Сумма (1) называется интегральной суммой функции 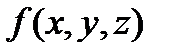 по области V.
по области V.
Обозначим через  максимальный диаметр элементарной области
максимальный диаметр элементарной области  (максимальное расстояние между точками этой области).
(максимальное расстояние между точками этой области).
Определение. Если существует конечный предел интегральной суммы (1) при 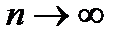 (
( ) и он не зависит ни от способа разбиения области V на элементарные области, ни от выбора точек
) и он не зависит ни от способа разбиения области V на элементарные области, ни от выбора точек  в них, то этот предел называется тройным интегралом от функции
в них, то этот предел называется тройным интегралом от функции 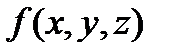 по области V и обозначается
по области V и обозначается  или
или  .
.
Таким образом, по определению, имеем
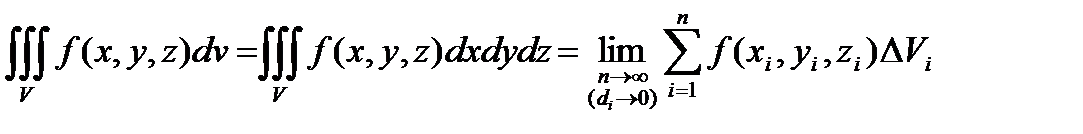 . (2)
. (2)
Теорема. Если функция  непрерывна в ограниченной замкнутой области V, то предел интегральной суммы (2) при
непрерывна в ограниченной замкнутой области V, то предел интегральной суммы (2) при 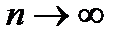 (
( ) существует и не зависит ни от способа разбиения области V на элементарные части, ни от выбора точек
) существует и не зависит ни от способа разбиения области V на элементарные части, ни от выбора точек  в них.
в них.
Свойства тройного интеграла аналогичны свойствам двойного интеграла.
1.  .
.
2.  .
.
3.  =
= 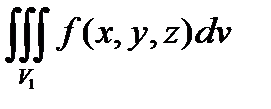 +
+  , где
, где 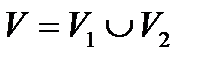 , а пересечение областей
, а пересечение областей 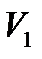 и
и  состоит из границы, их разделяющей.
состоит из границы, их разделяющей.
4. Если в области интегрирования  , то и
, то и  ; если в области V функция
; если в области V функция  , то и
, то и  .
.
5. Если в области V функция  , то
, то  , где V – объем области интегрирования.
, где V – объем области интегрирования.
6.  , где m и M – наименьшее и наибольшее значения функции
, где m и M – наименьшее и наибольшее значения функции  в области V.
в области V.
7. (теорема о среднем значении). Если функция  непрерывна в замкнутой области V, то в этой области существует точка
непрерывна в замкнутой области V, то в этой области существует точка 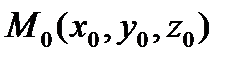 , такая что
, такая что  где V – объем области интегрирования.
где V – объем области интегрирования.
п.2. Вычисление тройного интеграла в декартовой системе координат
В декартовой системе координат вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.
Пусть область интегрирования V ограничена снизу поверхностью  , сверху – поверхностью
, сверху – поверхностью  (
( ), причем
), причем  и
и  – непрерывные функции в замкнутой области D, являющейся проекцией области V на плоскость Оxy.
– непрерывные функции в замкнутой области D, являющейся проекцией области V на плоскость Оxy.
 Пусть область V – правильная в направлении оси Оz, т.е. любая прямая, параллельная оси Оz, пересекает границу области не более чем в двух точках. Тогда для любой функции
Пусть область V – правильная в направлении оси Оz, т.е. любая прямая, параллельная оси Оz, пересекает границу области не более чем в двух точках. Тогда для любой функции 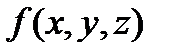 , непрерывной в области V, справедлива формула
, непрерывной в области V, справедлива формула
 . (3)
. (3)
Таким образом, вычисление тройного интеграла сводится к вычислению двойного интеграла от определенного (в скобках). При этом сначала вычисляется внутренний интеграл по переменной z (при этом x и y – const), а затем – двойной по области D. Результатом вычисления внутреннего интеграла является функция двух переменных: x и y.
Если область D ограничена линиями  , где
, где  и
и  – непрерывные на отрезке
– непрерывные на отрезке  функции, причем
функции, причем  , то, переходя в формуле (3) от двойного интеграла по области D к повторному, получим
, то, переходя в формуле (3) от двойного интеграла по области D к повторному, получим
 . (4)
. (4)
По формуле (4) вычисляется тройной интеграл в декартовых координатах.
Замечания.
1. Аналогичным образом вычисляется тройной интеграл и в том случае, когда область интегрирования является правильной в направлении осей Оx и Оy.
2. Если область V более сложная, чем рассмотренная выше, то ее следует разбить на конечное число областей, правильных в направлении какой-либо оси, и просуммировать результаты вычисления по этим областям.
3. Если область интегрирования – прямоугольный параллелепипед, задаваемый неравенствами 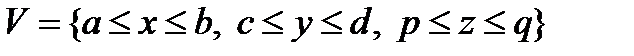 , то
, то
 . (5)
. (5)
Пример 1. Вычислить 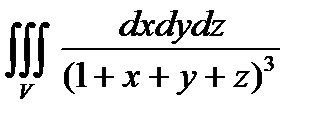 , где область V ограничена поверхностями
, где область V ограничена поверхностями  .
.
 Решение. Чтобы найти интеграл, необходимо понимать, как выглядит область интегрирования V. Построим ее. Уравнения
Решение. Чтобы найти интеграл, необходимо понимать, как выглядит область интегрирования V. Построим ее. Уравнения  определяют в пространстве
определяют в пространстве  координатные плоскости Оyz, Оxz и Оxy соответственно, уравнение
координатные плоскости Оyz, Оxz и Оxy соответственно, уравнение  – плоскость, проходящую через точки
– плоскость, проходящую через точки  и
и  . Область интегрирования V представляет собой тетраэдр. Область V является правильной в направлении оси Оz (как и в направлении осей Оx и Оy). Её проекция на плоскость Оxy – треугольник ОАВ, является правильной в направлении оси Оy (и оси Оx). В области V справедливы неравенства
. Область интегрирования V представляет собой тетраэдр. Область V является правильной в направлении оси Оz (как и в направлении осей Оx и Оy). Её проекция на плоскость Оxy – треугольник ОАВ, является правильной в направлении оси Оy (и оси Оx). В области V справедливы неравенства  . Тогда, согласно формуле (4), имеем:
. Тогда, согласно формуле (4), имеем:



 .
.
Пример 2. Вычислите 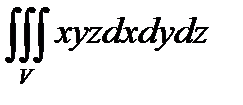 , если область V ограничена сферой
, если область V ограничена сферой  и плоскостями
и плоскостями  (первый октант).
(первый октант).
Решение. Область V ограничена снизу плоскостью  и сверху – поверхностью
и сверху – поверхностью  Изобразим проекцию области V на плоскость Oxy.
Изобразим проекцию области V на плоскость Oxy.
| х |
| у |
| 0 |
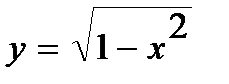
|



 .
.