Задания для выполнения контрольной работы №2.

Задание 1

321-340. Найти общее решение дифференциального уравнения.

321. 322.

323. 324.

325. 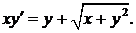326.

327 328

329. 330.

Задание 2

381-390. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость

381.

382.

383.

384.

385.

386.

387.

388.

389.

390.

Задание 3

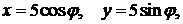391. Вычислить криволинейный интеграл вдоль окружности обходя ее против хода часовой стрелки. Сделать чертеж.

392. Вычислить криволинейный интеграл вдоль параболы от точки А(1;1) до точки В(2;4). Сделать чертеж.

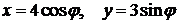393. Вычислить криволинейный интеграл вдоль эллипса , обходя его против хода часовой стрелки. Сделать чертеж.

394. Вычислить криволинейный интеграл вдоль параболы 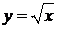от точки А(1;1) до точки В(4;2). Сделать чертеж.

395. Вычислить криволинейный интеграл от точки до точки 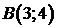вдоль прямой, проходящей через эти точки. Сделать чертеж.

396. Вычислить криволинейный интеграл от точки до точки вдоль прямой проходящей через эти точки. Сделать чертеж.

397. Вычислить криволинейный интеграл от точки до точки вдоль прямой, проходящей через эти точки. Сделать чертеж.

398. Вычислить криволинейный интеграл вдоль кривой от точки до точки . Сделать чертеж.

399. Вычислить криволинейный интеграл вдоль параболы от точки до точки . Сделать чертеж.

400. Вычислить криволинейный интеграл 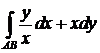вдоль кривой от точки до точки 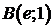. Сделать чертеж.

Задание 4

431-440. Найти интервал сходимости степенного ряда

431. 432.

433 434.

435. 436.

437. 438.

439. 440.

Задание 5

461-470. Разложить данную функцию в ряд Фурье в интервале

461. в интервале

462. в интервале

463. в интервале

464. в интервале

465. в интервале

466. в интервале

467. 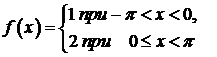в интервале

468. в интервале

469. Функция задана в интервале Разложить данную функцию в ряд Фурье в интервале 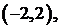продолжив ее в интервал четно.

470. Функция задана в интервале Разложить данную функцию в ряд Фурье в интервале 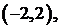продолжив ее в интервал нечетно.

Задание 6

521-530. Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющего заданным начальным условиям.

521.

522.

523.

524.

525.

526.

527.

528.

529.

530.

Методические рекомендации по выполнению заданий.

321-340. Найти общее решение дифференциального уравнения.

Пример 1.

381-390. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость

Пример: Вычислить V тела, ограниченного поверхностями .

Решение

Строим область интегрирования

x

 

или – это цилиндрическая поверхность, в основании которой лежит парабола, а образующие параллельны оси OZ.

- это плоскость, параллельная оси ОУ.

По формуле вычисления объема имеем:

.

Вычислим двойной интеграл. Для этого изобразим проекцию тела на плоскость ХОУ:

x

 

 

391-400. Решение криволинейного интеграла сводится к решению определенного интеграла, используя уравнения кривой.

Пример 1. Вычислить

вдолькривой от до 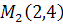(рис. 41).

Решение

 

Сведем данный криволинейный интеграл второго рода к определенному интегралу, используя уравнение кривой . Вычислим: 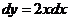. По условию переменная х изменяется от 1 до 2. Тогда

Пример 2. Вычислить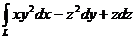

при перемещении по дуге винтовой линии

от точки пересечения с плоскостью z=0до точки пересечения с плоскостью z=1.

Решение

Сведем интеграл к определенному, используя уравнение кривой

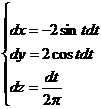
Найдем пределы интегрирования. По условию z=0 и z=1, тогда

Первый интеграл равен нулю, второй после двукратного применения формулы интегрирования по частям равен , третий равен .

Ответ: .

Если кривая замкнута, то криволинейный интеграл по такой кривой называется криволинейным интегралом по замкнутому контуру и обозначается . За положительный обход замкнутой кривой выбирается обход против часовой стрелки.

Пример 3. Вычислить криволинейный интеграл

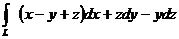
по замкнутой кривой ,

Решение

Замкнутая кривая ограничена тремя линиями АВ, ВС и СА, поэтому криволинейный интеграл по замкнутому контуру разобьется на сумму трех интегралов по каждой линии.

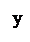
Сведем каждый криволинейный интеграл к определенному, используя уравнения кривых.

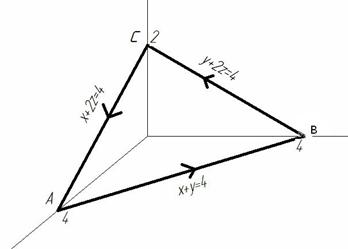
: кривая АВ расположена в плоскости ХОУ, следовательно , уравнение кривой , отсюда 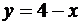, где , тогда

.

: кривая ВС расположена в плоскости УОZ, следовательно , уравнение кривой , отсюда , , , тогда

.

: кривая СА расположена в плоскости ХОZ, следовательно , уравнение кривой , отсюда , где , тогда

.

Окончательно: .

Ответ: 4.

Если вектор – функция задана на плоскости, то криволинейный интеграл второго рода по замкнутому контуру можно свести к двойному с помощью формулы Грина:

,

где область D – это область, которую ограничивает замкнутый контур L.

431-440. Найти интервал сходимости степенного ряда

461-470. Разложить данную функцию в ряд Фурье в интервале

521-530. Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющего заданным начальным условиям.