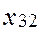Классическая транспортная задача
Имеется р пунктов производства (поставщики) и q пунктов потребления (потребители) некоторого однородного продукта.
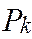 - объемы производства в пунктах производства k (k=1,…,p);
- объемы производства в пунктах производства k (k=1,…,p);
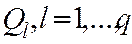 - объемы потребления в пунктах потребления l;
- объемы потребления в пунктах потребления l;
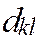 - затраты, связанные с перевозкой единицы продукта из пункта р производства в пункт q потребления.
- затраты, связанные с перевозкой единицы продукта из пункта р производства в пункт q потребления.
Требуется прикрепить пункты производства к пунктам потребления таким образом, чтобы суммарные расходы на транспортировку были минимальными.
Математическая модель
Пусть  - планируемый объем перевозок из пункта k в пункт l;
Найти матрицу (план перевозок) - планируемый объем перевозок из пункта k в пункт l;
Найти матрицу (план перевозок)
 удовлетворяющую условиям:
1.
удовлетворяющую условиям:
1.  ≥0, k=1,…,p; l=1,…,q
2. ≥0, k=1,…,p; l=1,…,q
2.  (суммарное количество продукции не превышает объемов производства) (суммарное количество продукции не превышает объемов производства)
 (удовлетворение спроса)
3. (удовлетворение спроса)
3. 
| Возможны случаи:
а)  - суммарные запасы превышают суммарные потребности
б) - суммарные запасы превышают суммарные потребности
б) 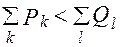 - суммарные потребности превышают суммарные запасы
в) - суммарные потребности превышают суммарные запасы
в)  - суммарный объем производства совпадает с суммарным объемом потребления
Размерность задачи: (р+ q) x (р ·q) - суммарный объем производства совпадает с суммарным объемом потребления
Размерность задачи: (р+ q) x (р ·q)
|
Математическая модель
Возможны случаи:
а)  - суммарные запасы превышают суммарные потребности
б) - суммарные запасы превышают суммарные потребности
б) 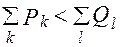 - суммарные потребности превышают суммарные запасы
в) - суммарные потребности превышают суммарные запасы
в)  - суммарный объем производства совпадает с суммарным объемом потребления - суммарный объем производства совпадает с суммарным объемом потребления
| Если имеют место случаи а) или б), модель называется открытой, в случае в) – закрытой.
 Открытая модель в закрытую:
Если имеет место случай а), вводится фиктивный потребитель Открытая модель в закрытую:
Если имеет место случай а), вводится фиктивный потребитель 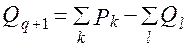 Если имеет место случай б), вводится фиктивный поставщик
Если имеет место случай б), вводится фиктивный поставщик  При этом стоимость перевозок объема продукции полагают равными нулю.
При этом стоимость перевозок объема продукции полагают равными нулю.
|
Классическая транспортная задача
Задача Т2
Пусть  , k=1,…,p; l=1,…,q
Найти план перевозок , k=1,…,p; l=1,…,q
Найти план перевозок 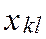 ,
удовлетворяющий условиям:
1. ,
удовлетворяющий условиям:
1.  ≥0, k=1,…,p; l=1,…,q
2. ≥0, k=1,…,p; l=1,…,q
2. 
 3.
3. 
| Задача Т2*
Определить вектор
 ,
удовлетворяющий условиям:
1. -
2. ,
удовлетворяющий условиям:
1. -
2.  3.
3. 
|
Признак оптимальности
Допустимый план перевозок 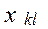 является оптимальным ↔ найдется вектор является оптимальным ↔ найдется вектор  , удовлетворяющий условию 2 задачи Т2*, что , удовлетворяющий условию 2 задачи Т2*, что
| |
 При этом вектор y является оптимальным в двойственной задаче.
При этом вектор y является оптимальным в двойственной задаче.
|
Оптимальное решение
Теорема. В классической транспортной задаче и двойственной к ней всегда существует оптимальная матрица  , k=1,…,p; l=1,…,q и оптимальный вектор
, k=1,…,p; l=1,…,q и оптимальный вектор  .
.
Классическая транспортная задача
Исходная информация Таблица 1

| 
| 
| … | 
|
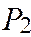
| 
| 
| … | 
|
| … | ||||

| 
| 
| … | 
|

| 
| … | 
|
Классическая транспортная задача (пример)
Исходная информация Таблица 2
 = 100 = 100
|

|

|
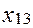
|

|
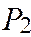 =120 =120
|

|

|

|
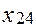
|
 =80 =80
|

|

|

|

|
 =70 =70
|  =90 =90
|  =85 =85
|  =55 =55
|
Выполнено условие: 100+120+80=70+90+85+55; р =3; q =4, размерность задачи:
(р+ q) x (р ·q)= 7 x 12
Классическая транспортная задача (пример)
При условии  , k =1,2,3; l= 1,2,3,4 найти план перевозок
, k =1,2,3; l= 1,2,3,4 найти план перевозок 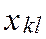 , удовлетворяющий условиям:
, удовлетворяющий условиям:
 ≥0, k= 1,2,3; l =1,2,3,4
≥0, k= 1,2,3; l =1,2,3,4


Матричная запись ограничений




Двойственная задача (пример)
Найти вектор
 :
:
1. –
2. 
 3.
3. 
Теорема
Среди р+q ограничений задачи Т2 одна строка (любая) линейно зависима от других.
Теорема
В оптимальном решении задачи Т2 не может быть более (р+q -1) ненулевых компонентов  , если оптимальное решение единственное.
, если оптимальное решение единственное.
(Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б. Математическое программирование:
-М.: Высшая школа, 1980. -300с.)
Замечание. В приведенном примере в оптимальном решении только 6 переменных могут быть ненулевыми, если оптимальное решение – единственное.
МПУ для классической транспортной задачи (метод потенциалов)
1 этап ( Построение допустимого базисного множества К ). Для построения исходного д.б.м. К применяется метод северо-западного угла. При этом полностью используются возможности поставщиков и полностью удовлетворяются потребности потребителей
Пример.
Исходные данные Метод северо-западного угла
| (1,1):  , ,  (1,2):
(1,2):  , , 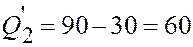 (2,2):
(2,2):  , ,  (2,3):
(2,3):  , ,  (3,3):
(3,3):  , ,  (3,4):
(3,4): 
|
Исходное допустимое решение, д.б. м. К
1 этап. Получили исходное допустимое решение по методу северо-западного угла:
| занятая клетка[1] | _ свободная клетка | _ | ||
| _ | _ | |||
| _ | _ | |||
К ={(1,1); (1.2); (2,2); (2,3); (3,3); (3,4)} – допустимое базисное множество
 , остальные элементы матрицы равны 0. Количество ненулевых компонент (занятых клеток) р+q -1=6, µ(x)=-7875
, остальные элементы матрицы равны 0. Количество ненулевых компонент (занятых клеток) р+q -1=6, µ(x)=-7875
Двойственный вектор
2 этап.
Находится двойственный вектор y (K):

| К ={(1,1); (1.2); (2,2); (2,3); (3,3); (3,4)} – допустимое базисное множество (6 уравнений, 5 неизвестных, полагаем  ) )
 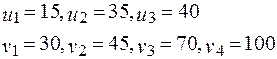 
|
Проверка двойственной допустимости б.м. К
2 этап.
Если вектор y (K) – допустимый в двойственной задаче, т.е.
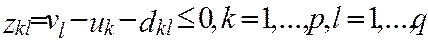 ,
то соответствующее ему д.б.м. К является д.д.б.м. ,
то соответствующее ему д.б.м. К является д.д.б.м.
| К ={(1,1); (1.2); (2,2); (2,3); (3,3); (3,4)} – допустимое базисное множество
   y (K)=(15,35,40,30,45,70,100)
y (K)=(15,35,40,30,45,70,100)
 Условие нарушается для (1,3) и (1,4)
Условие нарушается для (1,3) и (1,4)
|
Выбор элемента для ввода в д.б.м. К
2 этап.
Условие нарушается для (1,3) и (1,4)
Выбираем (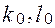 ): ): 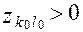 , ,  (
(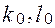 )=(1,4)
Вычисляем коэффициенты разложения вектора )=(1,4)
Вычисляем коэффициенты разложения вектора
 по базисным векторам:
по базисным векторам:

|   = =  Элемент (1,4) вводится в д.б.м. К
Элемент (1,4) вводится в д.б.м. К
    Среди
Среди  есть положительные, определим элемент, выводимый из базиса. есть положительные, определим элемент, выводимый из базиса.
|