Определение моментов инерции тел вращения
методом крутильных колебаний.
Учебно-методическое пособие
К лабораторной работе № 1.3
Владивосток
УДК53(о76.5)
ББК 22.36
0-60
Определение моментов инерции тел вращения
0-60 методом крутильных колебаний. Проверка теоремы Гюйгенса – Штейнера.
0-61 Учебно-методическое пособие к лабораторной работе № 1.3 по дисциплине «физический практикум»// сост. В.Е.Полищук,Р.Ф.Полищук. – Владивосток: Издательский дом Дальневост. федерал.ун-та, 2013-с.12.
Пособие, подготовленное на кафедре общей физики Школы естественных наук ДВФУ, содержит методические указания к выполнению лабораторной работы по механике с целью экспериментального изучения момента инерции твердых тел вращения ипроверки теоремы Гюйгенса-Штейнера.
Для студентов ДВФУ всех специальностей.
УДК 53(076.5)
ББК 22.36
Составители Полищук В.Е.
Полищук Р.Ф.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего профессионального образования
«Дальневосточный федеральный университет»
(ДВФУ)
Школа естественных наук
Определение моментов инерции тел вращения методом
крутильных колебаний.
Проверка теоремы Гюйгенса-Штейнера.
Учебно-методическое пособие к лабораторной работе №1.3
По дисциплине «физический практикум»
Владивосток
Издательский дом Дальневосточного федерального университета
Целью данной лабораторной работы является изучение законов динамики вращательного движения твердого тела, экспериментальное измерение момента инерции простейших тел вращения и проверка теоремы Гюйгенса-Штейнера.
Основные понятия вращательного движения твердого тела .
Кроме понятия материальной точки, в механике используется модельное понятие абсолютно твердого тела – тела, деформациями которого в условиях данной задачи можно пренебречь. Такое тело можно рассматривать как систему жестко закрепленных материальных точек.
Вращательным движением твердого тела называется движение, при котором все точки тела описывают окружности, центры которых лежат на одной прямой, называемой осью вращения тела. При вращательном движении все точки тела движутся с одной и той же угловой скоростью и угловым ускорением и совершают одинаковые угловые перемещения. Однако, как показывает опыт, при вращательном движении твердого тела вокруг закрепленной оси, масса уже не является мерой его инертности, а сила – недостаточна для характеристики внешнего воздействия. Кроме того, опыты показывают, что ускорение при вращательном движении зависит не только от массы тела, но и от ее распределения относительно оси вращения; зависит не только от силы, но и от точки ее приложения и направления действия. Поэтому, для описания вращательного движения твердого тела введены новые динамические характеристики такие, как момент силы, момент импульса и момент инерции тела. При этом следует иметь в виду, что существует два разных понятия этих величин: относительно оси и относительно любой точки О (полюса, начала), взятой на этой оси.
Моментом силы 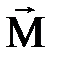 относительно неподвижной точки О называется векторная величина, равная векторному произведению радиус-вектора
относительно неподвижной точки О называется векторная величина, равная векторному произведению радиус-вектора 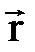 проведённого из точки О в точку приложения результирующей силы
проведённого из точки О в точку приложения результирующей силы  , на вектор этой силы:
, на вектор этой силы:

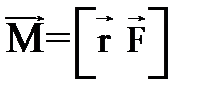 (1)
(1)
 Вектор момента силы
Вектор момента силы 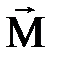 всегда перпендикулярен плоскости, в которой расположены вектора
всегда перпендикулярен плоскости, в которой расположены вектора 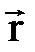 и
и  , а его направление относительно этой плоскости определяется правилом буравчика. Согласно правила правого буравчика (рис.2), при вращении его ручки в направлении от
, а его направление относительно этой плоскости определяется правилом буравчика. Согласно правила правого буравчика (рис.2), при вращении его ручки в направлении от 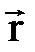 к
к  в направлении меньшего угла a, поступательное движение буравчика определит направление вектора
в направлении меньшего угла a, поступательное движение буравчика определит направление вектора 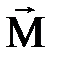
Вектора, направление которых связывают с направлением вращения (угловая скорость, угловое ускорение, момент силы, момент импульса и т.п.), называют псевдовекторами или аксиальными в отличие отобычных векторов (скорость, радиус-вектор, ускорение и т.п.), которые называют полярными или истинными.
Величина вектора момента силы (численное значение момента силы) определяется согласно формуле векторного произведения, т.е. 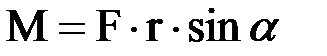 , где a- угол между направлениями векторов
, где a- угол между направлениями векторов 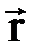 и
и  . Величина p= r·Sinα называется плечом силы (рис.2). Плечо силы р - это кратчайшее расстояние от точки О до линии действия силы
. Величина p= r·Sinα называется плечом силы (рис.2). Плечо силы р - это кратчайшее расстояние от точки О до линии действия силы 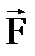 . Следовательно, величину момента силы можно найти как произведение силы на ее плечо:M=Fp.
. Следовательно, величину момента силы можно найти как произведение силы на ее плечо:M=Fp.
Моментом силы относительно оси, называется проекция на эту ось вектора момента силы, найденного относительно любой точки, принадлежащей этой оси. Ясно, что относительно оси момент силы является скалярной величиной. В системе СИ момент силы измеряется в Н·м
Мерой инертности тел при поступательном движении является их масса. Инертность же тел при вращательном движении зависит не только от массы тела, но и от ее распределения в пространстве относительно оси вращения. Мерой инертности тела при вращательном движении является момент инерции тела I относительно оси вращения или точки. Момент инерции, как и масса, величина аддитивная, скалярная.
Моментом инерции тела относительно оси вращения называется физическая скалярная величина, равная сумме произведений масс материальных точек (на которые можно разбить все тело) на квадратырасстояний каждой из них до оси вращения:
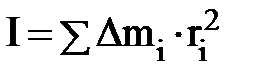 , (2)
, (2)
где I -момент инерции материальной точки.
В системе СИ момент инерции измеряется в кг·м2.
Момент инерции твердого тела зависит от массы тела, формы и размера тела.
Основной закон динамики вращательного движения твердого тела.
 I
I  =M. (3)
=M. (3)
Уравнение (3) называется основным уравнением динамики вращательного движения твердого тела относительно оси. Так как  =
= 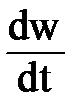 , а момент инерции тела относительно данной оси вращения является постоянной величиной и, следовательно, его можно внести под знак дифференциала, то уравнение (3) можно записать в виде:
, а момент инерции тела относительно данной оси вращения является постоянной величиной и, следовательно, его можно внести под знак дифференциала, то уравнение (3) можно записать в виде:
 . (4)
. (4)
ВеличинаIw=L (5)
называется моментом импульса тела относительно оси. C учетом (5) уравнение (4) можно записать в виде:
 (6)
(6)
Уравнения (3-6) носят скалярный характер, и применяются только для описания вращательного движения тел относительно оси. При описании вращательного движения тел относительно точки (или полюса, или начала), принадлежащей данной оси, указанные уравнения соответственно записываются в векторном виде:
 (3*);
(3*); 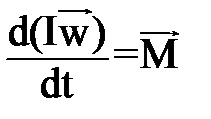 (4*);
(4*); 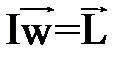 (5*);
(5*);  (6*).
(6*).
При сравнении уравнений поступательного и вращательного движений тела видно, что при вращательном движении вместо силы в уравнениях стоит ее момент, вместо массы тела – момент его инерции, вместо импульса (или количества движения) – момент импульса (или момент количества движения).
Из уравнений (6) и (6*) вытекает закон сохранения момента импульса твердого тела как относительно оси, так и относительно точки. Из уравнения (6) следует: если суммарный момент всех внешних сил М относительно оси равен нулю(M=0, следовательно и dL=0), то момент импульса этого тела относительно оси его вращения остается постоянной величиной (L=Const).
В данной лабораторной работе определяются моменты инерции для простейших тел вращения. Под телом вращения понимается объемное тело, возникающее при вращении плоской фигуры, ограниченной произвольной кривой, вокруг оси, лежащей в той же плоскости. Тело вращения всегда имеет ось симметрии. Простейшими примерами тел вращения являются:
шар – образован полукругом, вращающимся вокруг диаметра разреза;
цилинд р – образован прямоугольником,вращающимся вокруг одной из его сторон;
конус – образован прямоугольным треугольником, вращающимся вокруг одного из его катетов и т.п.
В рассматриваемой лабораторной работе методом крутильных колебаний определяются моменты инерции для тел: сферы, диска, стержня,полого и сплошного цилиндров. Кроме того, экспериментально проверяется теорема Гюйгенса-Штейнера. Эта теорема позволяет определить момент инерции тела относительно любой оси, не проходящей через центр массы тела, если известен момент инерции данного тела относительно оси проходящей через центр масс и параллельной относительно искомой оси.
Теорема Гюйгенса-Штейнера. Момент инерции тела относительно любой оси, не проходящей через центр массы данного тела, равен моменту инерции этого тела относительно оси, проходящей через его центр массы и параллельной первой оси, плюс произведение массы данного тела на квадрат расстояния между этими осями:I = Io+mɑ2, где I – момент инерции тела относительно искомой оси, (не проходящей через центр массы тела), Iо момент инерции тела относительно оси проходящей через центр массы и параллельной первой оси, m- масса тела, ɑ - расстояние между осями.
Вывод рабочей формулы для расчета момента инерции тел вращения методом крутильных колебаний.
Крутильный маятник в данной работе состоит из спиральной пружины,закрепленной в штативе. С пружиной жестко скреплена ось, свободно вращающаяся в штативе. На ось крепится тело, момент инерции которого определяется. Если эту систему вывести из положения равновесия, повернув тело на некоторый угол φ и отпустить, то возникнут крутильные колебания тела. При крутильных колебаниях на тело действует возвращающий момент силы, приостанавливающий отклонение тела от состояния равновесия, а затем сообщающий телу обратное движение. Возвращающий момент силы М обусловлен упругими силами, возникающими в спиральной пружине.
Как показывают эксперименты,в области упругих деформаций кручения, угол поворота 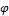 спиральной пружины прямо пропорционален проекции момента силы М на ось вращения z (Мz), т.е.
спиральной пружины прямо пропорционален проекции момента силы М на ось вращения z (Мz), т.е.
Мz = -G·φ (7).
Коэффициент пропорциональности G называется угловым коэффициентом упругости спиральной пружины. Из уравнения (3) следует:Мz = Iz·  ,где
,где  =
= 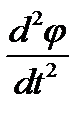 - угловое ускорение, Iz – момент инерции тела относительно вращающейся оси установки. Следовательно,
- угловое ускорение, Iz – момент инерции тела относительно вращающейся оси установки. Следовательно,
Мz = Iz· 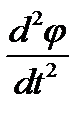 (8).
(8).
Из (7) и (8) следует равенство: Iz· 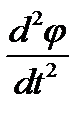 = - G·φ. Или
= - G·φ. Или
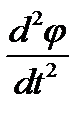 +
+  =0 (9)
=0 (9)
Уравнение (9) является дифференциальным уравнением гармонических колебаний, которое можно переписать в следующем виде
 +ω2φ = 0, (10)
+ω2φ = 0, (10)
где ω2 =  (11)
(11)
Уравнение (10) описывает колебания крутильного маятника относительно его положения равновесия. Из решения дифференциального уравнения (10) следует, что колебания крутильного маятника являются гармоническими φ = φо·Sin(ω·t +α), где φо – амплитуда углового смещения, равная начальному угловому отклонению маятника, а ω- циклическая частота колебаний, которая связана с периодом колебаний соотношением
ω=  (12)
(12)
Из уравнений (11) и (12) вытекает рабочая формула экспериментального определения момента инерцииIz для предложенных тел вращенияи проверки теоремы Гюйгенса – Штейнера:
Iz=I= 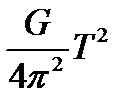 , (13)
, (13)
Подготовкаи выполнение лабораторной работы.

Рис.3Общий вид экспериментальной установки и исследуемых тел.
Как видно из рабочей формулы (13) основными параметрами при экспериментальном определении моментов инерции указанных выше тел, является период колебаний тела Т и угловой коэффициент упругости спиральной пружиныG. В данной лабораторной работе угловой коэффициент экспериментально уже определен и имеет значение 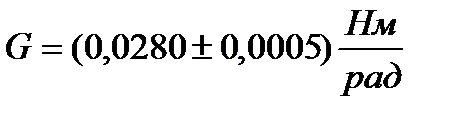 .
.