ЛЕКЦИЯ 6
6.1 Определения бесконечнобольшой функциив точке 
,
Определение 6.1. Функция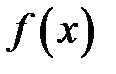 
называется бесконечно большой в точке , если 
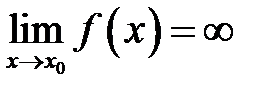, т.е. для любого, сколь угодно большого числа 
найдется такое число 
, что для всех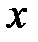 
, удовлетворяющих неравенству 
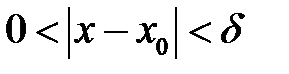, следует, что 
.
Теорема 6.1. Если функция 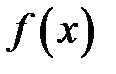– бесконечно большая в точке , то функция 
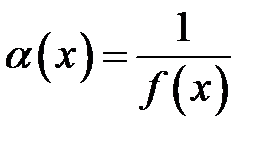является бесконечно малой в точке .
Теорема 6.2. Если функция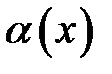 
– бесконечно малая в точке и отлична от нуля в окрестности этой точки, т.е. длявсех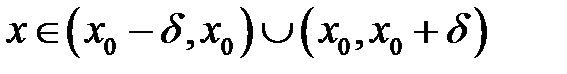 
для некоторого числа 
, то функция 
является бесконечнобольшой в точке .
Теорема 6.3 (о связи функции, имеющей конечный предел и бесконечно малой функцией при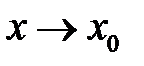 
).
Пустьфункция 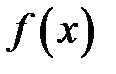определена в некоторой окрестности точки , за исключением может быть самой точки . Тогда для того, чтобы существовал конечный предел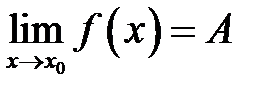 
, необходимо и достаточно, чтобы функцию 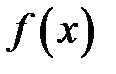можно было представить в виде 
, где 
– бесконечно малая в точке .
Доказательство. Необходимость. Пустьфункция 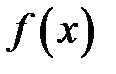имеет конечный предел 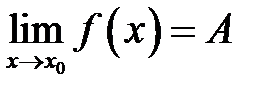. Это эквивалентно, тому, что 
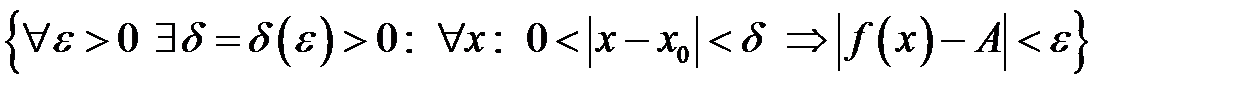. Обозначим 
. Отсюда .
Неравенство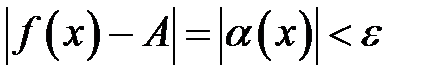 
говорит о том, что – бесконечно малая в точке .. Следовательно, .
Достаточность. Пустьфункцию 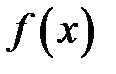можно было представить в виде , где А – постоянная (число), а – бесконечно малая в точке . Тогда 
. Подставим в последнее неравенство вместо ее выражение 
. Получили: 
, что эквивалентно тому, что 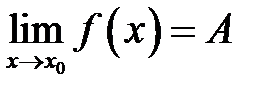, что и требовалось.
6.2 Определениянепрерывной функции
Определение 6.2. Функция 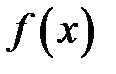называется непрерывной в точке , если выполняются три условия:
1) эта функция определена в некоторой окрестности точки ;
2) существует предел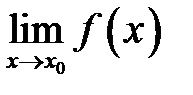 
;
3) этот предел равен значению функции в точке , т.е.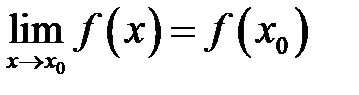 
.
На языке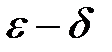 
условие 3) эквивалентно условию: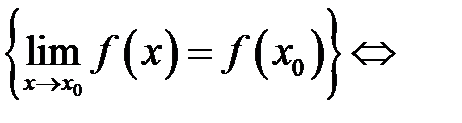 
.
Часто приходится рассматривать непрерывность функции в точке справа и слева.
Определение 6.3. Пусть функция 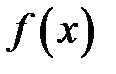определена в точке . Если 
, то говорят, что функция 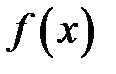непрерывна в точке слева. Если 
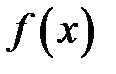, то функция непрерывна в точке справа.
Определение 6.4. Если функция непрерывна в каждой точке некоторой интервала 
, то она называется непрерывной в этоминтервале.
Функция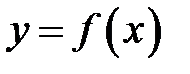 
называется непрерывной на отрезке 
, если она непрерывна во всех точках интервала , непрерывна справа в точке 
и непрерывна слева в точке 
.
Определение 6.5. Пусть функция 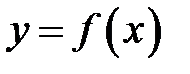определена на отрезке 
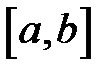. Возьмём произвольную точку 
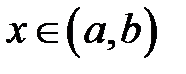. Близкая к ней другая точка 
может быть записана в виде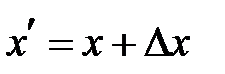 
, где число 
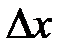называется приращением аргумента 
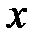. Оно может быть положительным или отрицательным. Разность 
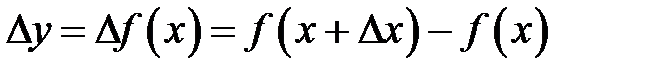называется приращением функции 
в точке 
, соответствующим приращению 
.
Определение 6.6. Функция называется непрерывной в точке , если она определена в некоторой окрестности этой точки, в том числе в самой точке , и если ее приращение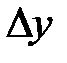 
в этой точке, соответствующее приращению аргумента 
, стремится к нулю,при 
.
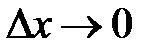Из этого определения следует, что если независимая переменная 
приближается к точке 
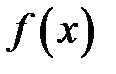, то значения функции неограниченно приближаются к значению функции в точке . При этом близким значениям аргумента соответствуют близкие значения функции. Поэтому графиком непрерывной функции является нигде не прерывающаяся линия.
Определение 6.5 утверждает, что 
. Получили, что 
. Если положить: 
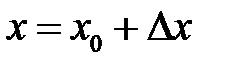, тогда из условия 
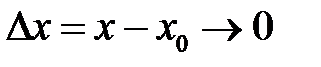следует 
, и определение 6.5 эквивалентно определению 6.1.