Пример решения классической транспортной задачи средствами MathCad

Лабораторная работа № 3

Задача. От ГПП промышленного предприятия, расположенной в узле 1, будет осуществляться электроснабжение цехов, расположенных в узлах 2, 3 и 4 (рисунок 3.1). Требуется найти оптимальную по критерию денежных затрат схему электрической сети.

Расчетные мощности всех узлов S_i и затраты c_ij на передачу единицы мощности по линии между узлами i и j приведены в таблице 3.1.

Решение задачи выполнить с учетом транзита мощности через нагрузочные узлы.

Рисунок 3.1

 

Таблица 3.1

№ вар	Si, МВА	cij, у.е./МВА
S 1	S 2	S 3	S 4	c 12	c 13	c 14	c 23	c 24	c 34
					1,0	1,0	2,2	1,8	2,1	1,0
					1,0	2,1	1,0	2,4	1,5	1,0
					2,1	1,0	1,0	2,3	1,0	1,2
					1,0	1,0	2,1	1,4	1,0	2,3
					2,2	1,0	1,0	1,0	2,1	1,5
					3,4	1,0	2,3	1,2	1,0	1,0
					1,0	2,3	3,3	1,0	1,4	1,0
					2,2	3,3	1,0	1,0	1,0	1,3
					1,0	3,4	2,3	1,2	1,0	1,0
					3,3	2,1	1,0	1,0	1,3	1,0

 

 

Методические указания к решению задачи.

 

Поставленная задача относится к классу транспортных задач с транзитом мощности через узлы.

Минимизируемая целевая функция в такой задаче имеет вид:

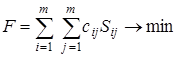, i ¹ j (3.1)

где S_ij – мощность, протекающая между узлами i и j;

m – количество узлов в схеме.

Ограничениями в транспортной задаче являются балансы мощности в узлах электрической сети.

Для решения задачи строим транспортную квадратную матрицу размерностью m (таблица 3.2). Справа от матрицы располагаем дополнительный столбец, в котором указывается заданная мощность источника питания S_i, а мощности нагрузочных узлов принимаются равными нулю (столбец источников). Снизу от матрицы располагаем дополнительную строку, в которой указываются заданные мощности нагрузок S_j, а мощность источника питания принимается равной нулю (строка нагрузок).

Каждая ij ячейка матрицы соответствует мощности, передаваемой от узла i к узлу j. Величины этих мощностей будем записывать в середине верхней части каждой ячейке транспортной матрицы. В правой средней части каждой ячейки запишем удельные стоимости c_ij передачи мощности от узла i к узлу j. Следует учесть, что
c_ij = c_ji.

Каждая ii (диагональная) ячейка матрицы соответствует транзитной мощности через i -й узел. Удельная стоимость передачи через i -й узел транзитной мощности
c_ii = 0.

 

Таблица 3.2 – Итерация 0

	v 1 = 0	v 2 = с 12	v 3 = с 13	v 4 = с 14
u 1 = 0		S 12 = S 2	S 13 = S 3	S 14 = S 4	S 1= S 2+ S 3 +S 4
	с 12	с 13	с 14
		«–»	«+»
u 2 =- с 12					S 2 = 0
с 21		с 23	с 24
u 3 =- с 13					S 3 = 0
с 31	с 32		с 34
u 4 =- с 14					S 4 = 0
с 41	с 42	с 43
		1«+»	«–»
	S 1 = 0	S 2	S 3	S 4	F = с 12 S 12 + с 13 S 13 + с 14 S 14

 

Этап 1. Определение допустимого решения транспортной задачи.

Одним из допустимых решений транспортной задачи с одним источником питания является радиальная сеть (рисунок 3.2), для которой выполняются балансы мощности во всех узлах:

S ₁₂ + S ₁₃ + S ₁₄ = S ₁; S ₁₂ = S ₂; S ₁₃ = S ₃; S ₁₄ = S ₄, (3.2)

а транзитные мощности через узлы:

S ₁₁ = 0; S ₂₂ = 0; S ₃₃ = 0; S ₄₄ = 0. (3.3)

Рисунок 3.2

Соответствующие этому решению значения мощностей занесены в транспортную матрицу (таблица 3.2). Значение целевой функции, определяемое по выражению (3.1), составляет:

F = c ₁₂ S ₁₂ + c ₁₃ S ₁₃ + c ₁₄ S ₁₄ (3.4)

и занесено в правый нижний угол транспортной матрицы (таблица 3.2).

Оптимизацию полученного решения выполним методом потенциалов.

Этап 2. Вычисление потенциалов источников и потребителей; проверка критерия оптимальности плана перевозок.

2.1 Присвоим каждой строке транспортной матрицы потенциал u_i, а каждому столбцу – потенциал v_j. Эти потенциалы таковы, что для каждой базисной переменной (переменной не равной нулю) должно выполняться условие:

c_ij = u_i + v_j. (3.5)

Транзитные переменные S_ii, соответствующие диагональным ячейкам транспортной матрицы, независимо от того, какие они имеют значения (нулевые или ненулевые), считаются базисными. Для этих переменных также должно выполняться условие (3.5).

Имеем семь базисных переменных S ₁₂ = S ₂, S ₁₃ = S ₃, S ₁₄ = S ₄, S ₁₁ = 0, S ₂₂ = 0,
S ₃₃ = 0 и S ₄₄ = 0. Количество неизвестных потенциалов восемь. Для решения системы (3.5) следует задаться значением одного из потенциалов, например, принять u ₁ =0. Тогда остальные потенциалы однозначно определятся из системы уравнений (3.5). Потенциалы проставлены в таблицу 3.3, обозначенную как «Итерация 0».

2.2 Для всех свободных переменных (недиагональных равных нулю переменных) определим косвенные стоимости:

D _ij = u_i + v_j - с_ij. (3.6)

2.3 Проверим критерий оптимальности: если все косвенные стоимости отрицательны (D _ij < 0), то допустимое решение будет оптимальным.

При невыполнении критерия оптимальности, например, для свободной переменной S ₄₃, эта переменная переводится в разряд базисных. Соответственно одна из базисных переменных должна перейти в разряд свободных. Для этого строится цикл пересчета.

Этап 3. Построение улучшенной схемы электрической сети, для которой затраты меньше или, по крайней мере, равны затратам для предыдущей схемы.

3.1 Выбираем свободную ячейку с наибольшей положительной косвенной стоимостью (max(D _ij)). Например, такой оказалась ячейка 43.

В цикл войдут ячейки (4,3) (отмечается знаком «+»), (1,3) (отмечается знаком «–»), (1,4) (отмечается знаком «+»), (4,4) (отмечается знаком «–»):

S ₄₃ («+») ® S ₁₃ («–») ® S ₁₄ («+»), ® S ₄₄ («–»).

В транспортной матрице получен цикл, показанный в таблице 3.2 стрелками.

3.2 В отрицательных вершинах цикла выбирается минимальная величина поставки: .

Выбираем , поскольку увеличение переменной S ₄₃ ограничено уменьшением переменной S ₁₃ до нулевого значения. При S ₄₃ = S ₁₃ базисная переменная S ₁₃ становится свободной (равной нулю). Увеличение переменной S ₄₃ не ограничено уменьшением переменной S ₄₄, поскольку все транзитные переменные S_ii входят в решение транспортной задачи со знаком минус.

В вершинах цикла, отмеченных знаком «+», переменные увеличиваются . В вершинах цикла, отмеченных знаком «–», переменные уменьшаются.

После перевода переменной S ₄₃ в разряд базисных, а переменной S ₁₃ в разряд свободных получается новая транспортная матрица (таблица 3.3).

 

Таблица 3.3 – Итерация 1

	v 1 = 0	v 2 = с 12	v 3 = с 13	v 4 = с 14
u 1 = 0		S 12 = S 2		S 14 = S 4+ S 3	S 1= S 2+ S 3 +S 4
	с 12	с 13	с 14
u 2 =- с 12					S 2 = 0
с 21		с 23	с 24
u 3 =- с 13					S 3 = 0
с 31	с 32		с 34
u 4 =- с 14			S 43 = S 3	- S 44 = - S 3	S 4 = 0
с 41	с 42	с 43
	S 1 = 0	S 2	S 3	S 4	F = с 12 S 12 + с 14 S 14 + с 43 S 43

 

Этой матрице соответствует новая схема электрической сети (рисунок 3.3). Видно, что переменная S ₄₃ вошла в состав базисных переменных (в схеме появилась линия между узлами 4 и 3), а базисная переменная S ₁₃ стала свободной (в схеме исчезла линия между узлами 1 и 3). Через узел 4 идет транзитная мощность S ₄₄ = S ₃.

 

Рисунок 3.3

 

Для новой транспортной матрицы по системе уравнений (3.5) определяются потенциалы u_i и v_j строк и столбцов и для всех свободных переменных проверяется критерий оптимальности (D _ij < 0). При невыполнении этого условия для какой-либо свободной переменной вся вычислительная процедура повторяется. Выполнение
D _ij < 0 для всех свободных переменных указывает на то, что найдено оптимальное решение.

В процессе решения задачи после каждого пересчета транспортной матрицы следует записывать текущее решение в виде (3.2) и (3.3), приводить новую схему электрической сети и вычислять по выражению (3.1) новое значение целевой функции.

 

Пример решения классической транспортной задачи средствами MathCad

 

Задача: В проектируемой системе электроснабжения имеется два узла с источниками питания и три узла потребителей. Мощности источников составляют A ₁ = 50 и A ₂ = 30 е.м., а мощности потребителей - B ₁ = 20, B ₂ = 25 и B ₃ = 35 е.м. Удельные затраты на передачу мощностей по линиям между узлами источников и потребителей составляют c ₁₁ = 1,2; c ₁₂ = 1,8; c ₁₃ = 1,5; c ₂₁ = 1,6; c ₂₂ = 2,3; c ₂₃ = 2,1 у.е./е.м.

Требуется найти оптимальную по критерию денежных затрат схему электрической сети.

Решение: Вначале создаем векторы Si и Sp, в которых содержатся исходные данные источников питания А и мощности потребителей В (транспонированные строки введены в целях сокращения места для записи исходных данных) и матрицу стоимостей перевозок С.

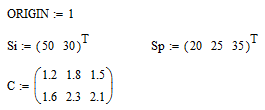
Затем фиксируем значения переменных;

Составляем целевую функцию, которая может быть представлена в виде следа (суммы диагональных элементов) произведения SC^Т, где Т – индекс транспонирования, записываем ее в такой форме:

Открываем вычислительный блок ключевым словом Given и задаем ограничения в матричном виде. С помощью встроенной функции Minimize (f, S) находим минимальное значение целевой функции f.

Блок решений может быть также записан в виде:

Векторы S1i и Sp1 введены для того, чтобы ограничения транспортной задачи записать в матричном виде. Например, для системы ограничений, представляющих собой балансы мощности в узлах источников питания:

мы получаем матричное уравнение S×S1i = Si. Аналогично вместо системы ограничений, представляющих собой балансы мощности в узлах потребителей, получаем матричное уравнение S^Т×S1p = Sp.