Функциональные ряды
ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ФУНКЦИОНАЛЬНЫХ РЯДОВ
Определение 1. Выражение вида
, (1.1)
где 
- функции переменной 
, называется функциональным рядом.
Определение 2. Областью определения функционального ряда называется пересечение областей определения его членов.
Так, областью определения ряда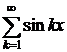 
является вся числовая прямая. Область определения ряда 
совпадает с множеством положительных чисел.
Придавая в (1.1) переменной 
определённые числовые значения из области определения ряда, мы получаем различные числовые ряды, которые могут оказаться сходящимися или расходящимися.
Определение 3. Точка 
из области определения ряда называется точкой сходимости функционального ряда (1.1), если числовой ряд
(
) 
() … 
() … (1.2)
сходится.
В противном случае называется точкой расходимости.
Определение 4. Совокупность тех значений , при которых функциональный ряд сходится, называется областью сходимости этого ряда.
Ясно, что область сходимости функционального ряда всегда является подобластью области определения этого ряда.
Очевидно, что в области сходимости ряда его сумма является некоторой функцией от , поэтому сумму функционального ряда обозначают через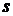 
().
Пример. Рассмотрим функциональный ряд
Этот ряд сходится при всех значениях , удовлетворяющих условию 
так как для каждого значения в интервале (-1;1) сумма ряда равна 
(сумма бесконечно убывающей геометрической прогрессии со знаменателем ). Таким образом, в интервале (-1;1) данный ряд определяет функцию
,
которая является суммой ряда, то есть
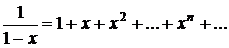
Отметим, что естественная область определения функции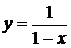 
шире области сходимости ряда 
Определение 5. Обозначим через 
сумму первых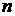 
членов ряда (1.1)
.
Если ряд (1.1) сходится и его сумма равна 
, то
,
где
Величина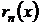 
называется остатком ряда (1.1).
Для всех значений в области сходимости ряда имеет место соотношение
,
поэтому
.
Определение 6. Функция 
называется представимой функциональным рядом (1.1) на некотором промежутке 
, если:
1) функциональный ряд сходится при любом из этого промежутка и имеет сумму ;
2) 
для любого 
.
Тот факт, что функция представима функциональным рядом, записывается так
.
МАЖОРИРУЕМЫЕ РЯДЫ
Определение. Функциональный ряд
(2.1)
называется мажорируемым в некоторой области изменения переменной , если существует такой сходящийся числовой ряд
(2.2)
с положительными членами, что для всех значений из данной области выполняются неравенства
(2.3)
Пример. Ряд 
мажорируем на всей числовой оси.
Действительно, для всех значений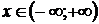 
а ряд
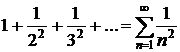
сходится.
Из определения следует, что ряд, мажорируемый в некоторой области, абсолютно сходится во всех точках этой области. Кроме того, мажорируемый ряд обладает следующим свойством.
Теорема. Пусть функциональный ряд
мажорируем на . Пусть - сумма этого ряда, 
– частичная сумма порядка 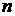. Тогда для любого сколь угодно малого числа 
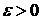найдётся независящее от положительное число 
такое, что для любого при всех 
будет выполняться неравенство
.
Доказательство. Обозначим через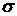 
сумму ряда (2.2)
,
тогда
,
где 
– сумма 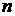первых членов ряда (2.2),
– сумма всех остальных членов этого ряда.
Так как этот ряд сходится, то
и, следовательно,
.
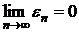Представим теперь сумму функционального ряда (2.1) в виде
,
где
,
Из условия (2.3) имеем
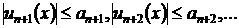
Поэтому
для любого .
Таким образом,
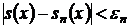
для всех , причём 
при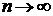 
.
Если мы возьмём 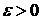, то найдётся номер такой, что при всех будет выполняться неравенство 
, а следовательно, и неравенство
.
Определение. Функциональный ряд называется равномерно сходящимся на , если для любого сколь угодно малого 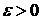найдётся такой номер , что для любого при всех будет выполняться неравенство
.
На основании теоремы следует, что мажорируемый ряд является рядом, равномерно сходящимся.
Пример 1. Ряд 
сходится на (-1;1). Для любого 
остаток ряда имеет вид
.
Очевидно, что
, 
.
Для всех одновременно неравенство
(если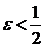 
)
при одном и том же 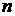невозможно. Сходимость данного ряда на (-1;1) неравномерна.
Пример 2. Ряд 
при любом 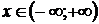сходится (он удовлетворяет условиям теоремы Лейбница). В условиях теоремы Лейбница остаток ряда оценивается по абсолютной величине модулем своего первого члена:
.
Значит, на всём бесконечном промежутке ряд сходится равномерно.
СВОЙСТВА ФУНКЦИОНАЛЬНЫХ РЯДОВ
I. Непрерывность суммы ряда
Рассмотрим ряд из непрерывных функций
сходящийся на некотором промежутке .
Известно, что сумма конечного числа непрерывных функций есть функция непрерывная. Для суммы ряда это свойство не сохраняется. Некоторые функциональные ряды с непрерывными членами имеют в качестве суммы непрерывную функцию, у других функциональных рядов с непрерывными членами сумма является разрывной функцией.
Пример. Рассмотрим функциональный ряд
Его члены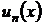 
являются непрерывными функциями при любом значении . Покажем, что этот ряд сходится, а сумма является разрывной функцией.
Частичная сумма порядка 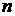этого ряда
.
Найдём сумму ряда:
1) если 
, то 
;
2) если 
, то 
;
3) если 
, то 
и 
Итак, имеем
Сумма рассматриваемого ряда есть функция разрывная.
Справедлива следующая теорема: всякий равномерно сходящийся ряд с непрерывными членами имеет в качестве суммы непрерывную функцию на рассматриваемом промежутке .
В частности, сумма ряда непрерывных функций, мажорируемого на некотором промежутке , есть функция, непрерывная на этом промежутке.
II. Интегрирование рядов
Теорема. Пусть ряд непрерывных функций
(3.1)
мажорируем на отрезке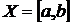 
, - сумма этого ряда. Тогда
(3.2)
где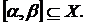 
Доказательство. Для определённости будем считать 
. Функцию можно представить в виде
где
Так как интеграл от суммы конечного числа слагаемых равен сумме интегралов от этих слагаемых, то
(3.3)
Так как ряд мажорируем, то при любом имеем
где при 
Поэтому
Так как при 
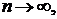то
Из (3.3) имеем:
Следовательно,
или
(3.4)
Выражение в квадратных скобках есть частичная сумма ряда
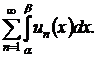
Частичные суммы этого ряда имеют предел, ряд сходится и его сумма в силу (3.4) равна 
то есть равенство (3.2) доказано.
Замечание. Если ряд (3.1) не мажорируем, то почленное интегрирование не всегда возможно.
III. Дифференцирование рядов
Теорема. Пусть ряд 
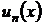где - функции, имеющие непрерывные производные на отрезке 
сходится на этом отрезке к сумме и ряд
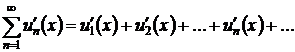(3.5)
мажорируется на том же отрезке, тогда
Доказательство. Обозначим через сумму ряда 
это будет непрерывная функция от 
Покажем, что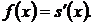 
Воспользуемся предыдущей теоремой, проинтегрируем ряд (3.5) почленно в промежутке 
где - произвольное значение из 
получим
Так как
то
По условию
поэтому по теореме об арифметических действиях со сходящимися рядами
Дифференцируя по обе части этого равенства, получим
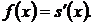
Теорема доказана.
Замечание. Требование мажорируемости ряда производных существенно, его невыполнение может привести к невозможности почленного дифференцирования ряда.
Рассмотрим в качестве примера ряд
Так как при любом
то ряд мажорируем и сходится на всей числовой прямой к непрерывной функции. Ряд 
составленный из производных, расходится, например, при . (Можно показать, что 
расходится не только при ).