Д. Р. Воденин
Численные методы оптимизации
Учебно-методическое пособие
Ульяновск 2016
УДК 519.83
ББК 22.183.41 я73
В 63
Печатается по решению Ученого совета
факультета математики, авиационных и информационных
технологий Ульяновского государственного университета
(протокол № от)
Рецензент:
А. Ю. Богданов ‑ к.ф.-м.н., доцент
Воденин Д. Р.
В 63 Численные методы оптимизации: учебно-методическое пособие / Д. Р. Воденин. – Ульяновск: УлГУ, 2016. ‑ 62 с.
В учебно-методическом пособии представлены численные методы одномерной оптимизации, многомерной оптимизации без ограничений и многомерной оптимизации с ограничениями.
Пособие предназначено для студентов направления математика и информатика, изучающих дисциплину методы оптимизации, факультета математики, информационных и авиационных технологий.
ã Воденин Д. Р., 2016
ã Ульяновский государственный университет, 2016
Оглавление
Глава 1. Одномерная оптимизация. 4
1.1. Основные понятия. 4
1.2. Классический подход. 6
1.3. Метод делания отрезка пополам. 7
1.4. Метод «золотого» сечения. 9
1.5. Метод Фибоначчи. 13
1.6. Симметричные методы.. 16
1.7. Метод Ньютона. 18
Глава 2. Многомерная оптимизация без ограничений. 18
2.1. Основные понятия. 18
2.2. Классический подход. 22
2.3. Классификация численных методов поиска экстремума функции нескольких переменных без ограничений. 24
2.4. Метод покоординатного спуска. 27
2.5. Метод Хука и Дживса(метод конфигураций). 29
2.6. Метод наискорейшего спуска. 31
2.7. Метод Флетчера -Ривса. 32
2.8. Эвристический выбор начального интервала одномерной минимизации. 33
2.9. Метод Давидона-Флетчера-Пауэлла. 35
2.10. Методы Ньютона и Ньютона-Рафсона. 36
2.11. О методе наименьших квадратов. 38
Глава 3. Многомерная оптимизация с ограничениями. 40
3.1 Классическая задача на условный экстремум. 40
3.2 Нелинейное программирование. 41
3.3 Классификация численных методов многомерной оптимизации
при наличии ограничений. 43
3.4 Метод внешних штрафных функций. 46
3.5 Метод барьерных функций. 48
3.6 Комбинированный метод штрафных функций. 51
3.7 Метод множителей. 53
3.8 Метод точных штрафных функций. 56
3.9 Метод проекции градиента. 58
Литература............................................................................................... 61
Глава 1. Одномерная оптимизация
1.1. Основные понятия
R - множество действительных(вещественных чисел).
. 
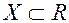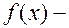функция определенная на множестве 
и принимающая во всех точках этого множества конечные значения.
Рассмотрим задачу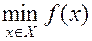 
Задача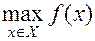 
сводится к данной заменой знака целевой функции. 
Определение 1. Точку 
назовем точкой минимума функции 
на множестве , если 
. Величину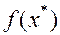 
назовем наименьшим или минимальным значение функции на множестве . 
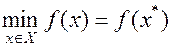
Множество всех точек минимума обозначим через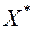 
Определение 2. Функция называется ограниченной снизу на множестве , если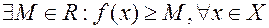 
Определение 3. Функция называется не ограниченной снизу на множестве , если 
Определение 4. Пусть функция ограничена снизу на множестве . Число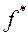 
назовем точной нижней гранью функции на множестве , если
1. 
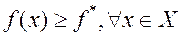
2. 
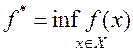
Определение 5. Последовательность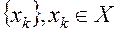 
называется минимизирующей для функции на множестве , если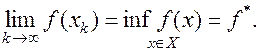 
Определение 6.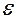 
окрестностью точки 
называется множество
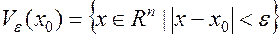
Определение 7..[2] Пусть функция определена и непрерывна на отрезке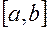 
.Назовем ее унимодальной на этом отрезке, если 
такие, что
1. строго монотонно убывает при 
(если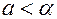 
)
2. строго монотонно возрастает пр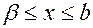и 
(если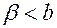 
)
3. 
при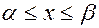 
Замечание. Случаи, когда один или два из отрезков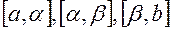 
вырождаются в точку не исключены.
1.2. Классический подход
Под классическим мы будем понимать тот подход, который основан на дифференциальном исчислении и подробно описан в учебниках по математическому анализу.
Пусть функция кусочно-непрерывна и кусочно-гладкая на отрезке 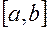. Тогда, как известно, точками экстремума могут быть лишь те точки, где выполняется одно из следующих условий:
1. либо терпит разрыв.
2. либо непрерывна, но ее производная терпит разрыв.
3. либо производна существует и 
.
4. либо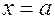 
или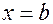 
.
Приведем без доказательства сначала необходимые, а потом достаточны условия существования экстремума.
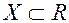Теорема 1. Пусть функция определена, непрерывна и дифференцируема на множестве .Если точка - точка локального минимума, то 
.
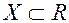Теорема 2. Пусть функция определена, непрерывна и дважды дифференцируема на множестве .Если точка - точка локального минимума, то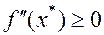 
.
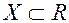Теорема 3. Пусть функция определена, непрерывна и дифференцируема на множестве . Если в точке - выполняются следующие условия:
1. .
2. 
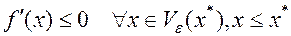и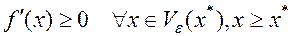 
то точка ‑ точка локального минимума.
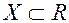Теорема 4. Пусть функция определена, непрерывна и дважды дифференцируема на множестве . Если в точке - выполняются следующие условия:
1. .
2. 
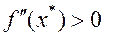то точка - точка локального минимума.
Теорема 5. Пусть функция определена, непрерывна и имеет на множестве 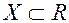непрерывные производные до порядка n включительно. Если в точке -: 
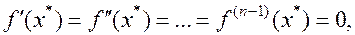а 
то точка - точка локального минимума если 
и не является точкой экстремума, если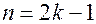 
.
2. 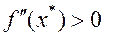то точка - точка локального минимума.
1.3. Метод деления отрезка пополам.
Простейшим методом минимизации функции одной переменной является метод деления отрезка пополам (метод дихотомии). Опишем его. Будем считать, что функция определена и унимодальна на отрезке 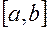. Пусть 
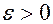требуемая точность вычислений, 
- параметр метода. Начинаем с выбора двух точек
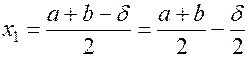(1.1)
. (1.2)
После этого вычисляем значения функции в этих точках и сравниваем между собой.
Если 
то полагаем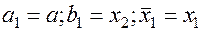 
; иначе
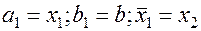
Так как функция определена и унимодальна на отрезке 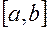, то ясно, что 
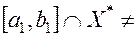Ø, а его длина равна
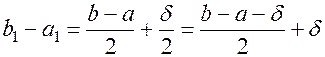(1.3)
Применим метод математической индукции. Пусть отрезок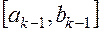 
уже известен, и его длина равна
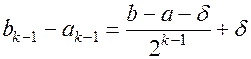(1.4)
Тогда на этом отрезке берем точки
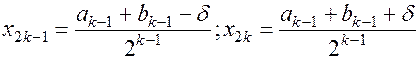, (1.5)
расположенные на отрезке 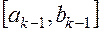симметрично относительно его середины и вычисляем значение функции в этих точках.
Если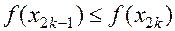 
то полагаем
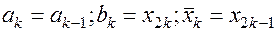; иначе
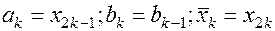
Длина получившегося отрезк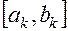а 
равна
(1.6)
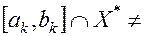Ø
Описанный процесс можно продолжать до тех пор пока не будет выполнено неравенство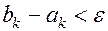 
, где 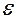- заданная точность. Отсюда имеем:
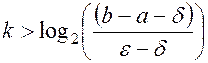(1.7)
Так как каждое деление пополам требует двух вычислений значений функции, то для достижения точности 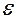потребуется всего
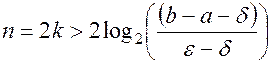таких вычислений.
После определения отрезка 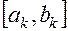в качестве приближения точки 
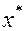выбираем 
- внутреннюю точку данного отрезка. При этом достигается максимальная абсолютная погрешность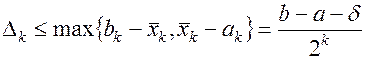 
(1.8)
Разумеется, можно вместо взять точку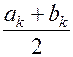 
, однако в этом случае для нахождения 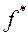требуется дополнительное вычисление функции.
1.4. Метод золотого сечения
Будем считать, что функция определена и унимодальна на отрезке 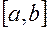. Пусть 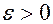требуемая точность вычислений.
Как известно, золотым сечением отрезка называется деление отрезка на две неравные части так, чтобы отношение длины всего отрезка к длине большей части равнялось отношению длины большей части к длине меньшей части отрезка.
Обозначим точку, делящую отрезок 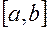в отношении золотого сечения через 
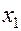. Тогда
(1.9)
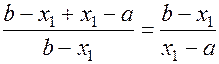
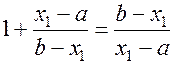
. Так как 
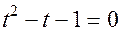
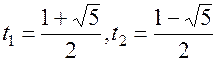
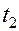-посторонний корень.
Получаем
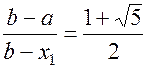
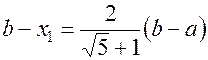
(1.10)
Очевидно, что точка 
, у которой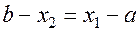 
также делит отрезок 
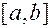в отношении золотого сечения.
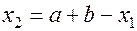(1.11)
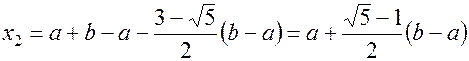
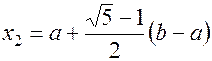(1.12)
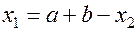(1.13)
Замечательно то, что точка 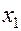в свою очередь делит отрезок 
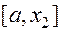в отношении золотого сечения. Так как 
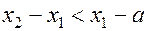и
.
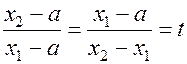Аналогично точка делит отрезок 
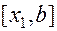в отношении золотого сечения. Опираясь на эти свойства, можно предложить следующий метод минимизации унимодальной функции на отрезке .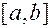
Положим 
На отрезке 
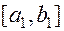.возьмем точки 
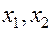, производящие золотое сечение отрезка, и вычислим 
Если то 
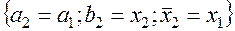иначе
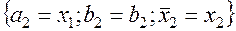
Поскольку функция унимодальна на отрезке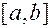 
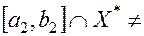Ø. Кроме того 
и при этом внутри отрезка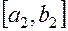 
находится точка 
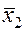, которая производит золотое сечение отрезка .
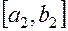Предположим, что уже найдены точки 
, вычислены значения функции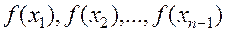 
, найден отрезок 
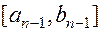, такой, что 
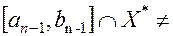Ø
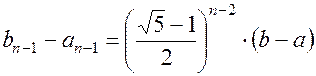(1.14)
и известна точка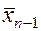 
производящая золотое сечение отрезка .
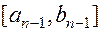Тогда в качестве следующей точки возьмем точку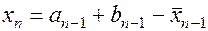 
также производящую золотое сечение отрезка 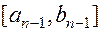. Пусть для определенности 
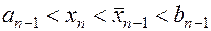. (Случай 
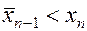рассматривается аналогично).
Если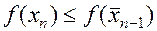 
то 
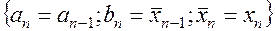иначе
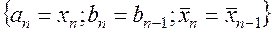
Новый отрезок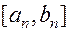 
таков, что 
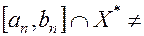Ø,
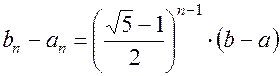, (1.15)
точка 
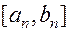производит золотое сечение отрезка и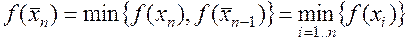 
. (1.16)
Итак, проводим описанную выше процедуру до тех пор пока не будет выполнено неравенство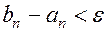 
, где 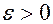- заданная точность.
После этого в считаем, что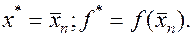 
при этом максимальная абсолютная погрешность
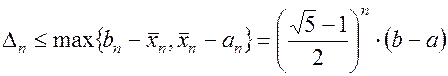(1.17)
1.5. Метод Фибоначчи.
Для реализации этого метода нам понадобятся числа Фибоначчи. Напомним, что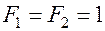 
. Остальные числа Фибоначчи определяются по формуле:
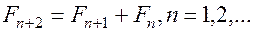(1.18)
Будем считать, что функция определена и унимодальна на отрезке 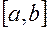. Пусть 
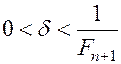- параметр метода.
Положим
Находим точки.
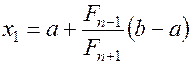(1.19)
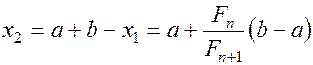(1.20)
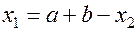(1.21)
На отрезке 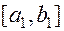.возьмем точки 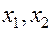, и вычислим
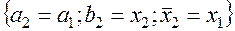Если то иначе
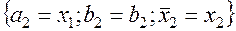
Поскольку функция унимодальна на отрезке 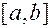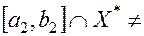Ø. Кроме того 
и при этом внутри отрезка 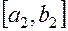находится точка .
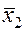С помощью метода математической индукции можно показать, что на k -ом шаге (k<n), когда вычислены значения функции в точках
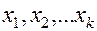и получен отрезок 
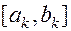,его длина будет
(1.22)
Причем точка (
со значением 
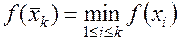совпадает с одной из точек:
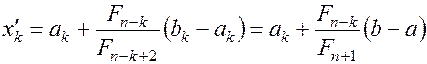(1.23)
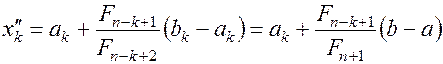(1.24)
Заметим, что 
; 
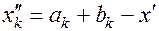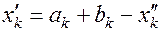. Расположены симметрично на отрезке 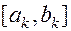относительно его середины.
Как видно из (1.23) и (1.24) при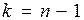 
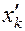точки 
и 
совпадают, то есть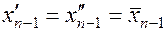 
совпадают с серединой отрезка 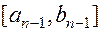. В заключение, нарушая симметричность процесса, 
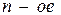вычислении функции проводится в точке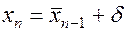 
(или точке 
) в зависимости от того, что требует метод.
Последний отрезок 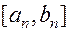таков, что 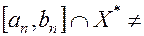Ø,
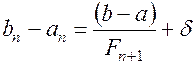, (1.25)
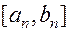точка является внутренней точкой отрезка и 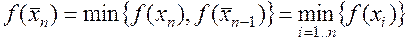. (1.26)
Следует подчеркнуть, что метод Фибоначчи для своей реализации требует, чтобы число n вычислений значений минимизируемой функции было задано заранее. Выбор первой точки 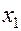в этом методе невозможен без знания n. В тех случаях, когда число n по каким-либо причинам не может быть задано заранее следует использовать метод золотого сечения.
Заметим, что
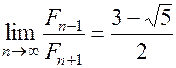(1.27)
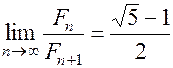(1.28)
А, значит, при больших n начальные точк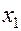и и методов Фибоначчи и золотого сечения практически совпадают.
1.6. Симметричные методы
Методы золотого сечения и Фибоначчи относятся к классу так называемых симметричны х методов. Дадим краткое описание симметричного метода минимизации унимодальной на отрезке 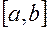функции .
Первый шаг. На отрезке 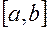выбирается точка 
.
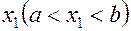Полагаем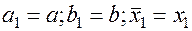 
.
Пусть уже сделано n-1 шагов и найдены отрезок 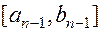и точка 
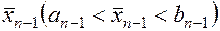, причем 
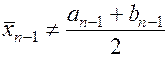. Тогда, на следующем n -ом шаге берется точка 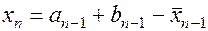, расположенная внутри отрезка 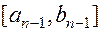симметрично точке 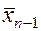относительно середины этого отрезка. Пусть для определенности 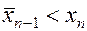(случай 
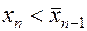рассматривается аналогично).
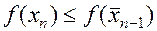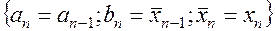Тогда, если то иначе
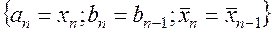
Новый отрезок 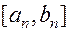таков, что 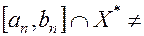Ø. Если
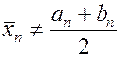, то процесс может быть продолжен. Если же 
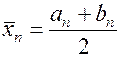, то процесс заканчивается. В этом случае при необходимости можно выбрать другую точку внутри полученного отрезка, отличную от середины и начать процесс сначала.
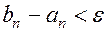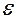Процесс заканчивается, если , где - заданная точность.
1.7. Метод Ньютона.
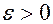Предположим, что функция определена и дважды непрерывно дифференцируема в некоторой окрестности точки . Пусть требуемая точность вычислений. Тогда Эту функцию можно представить в виде
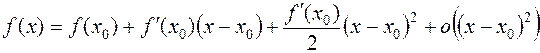(1.29)
Рассмотрим функцию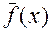 
являющейся квадратичной частью функции
в окрестности точки .
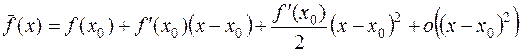(1.30)
В качестве приближения экстремума функции возьмем точку экстремума функции 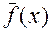. Найдем эту точку. Для этого находим производную функции 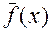и приравниваем ее к 0. Получаем.
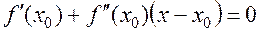(1.31)
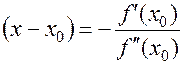
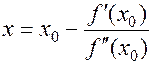(1.32)
Взяв найденную точку в качестве начальной продолжим этот процесс. Получаем:
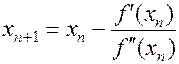(1.33)
Процесс будем заканчивать, когда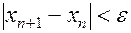 
Теорема 5. Пусть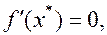 
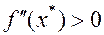и 
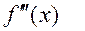непрерывна, то найдется такая окрестность 
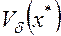точки , что если начальное приближение Ошибка! Объект не может быть создан из кодов полей редактирования., то последовательность 
построенная по методу Ньютона сходится к точке при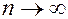 
.
Глава 2. Многомерная оптимизация без ограничений
2.1. Основные понятия
- n- мерное евклидово пространство. Точки этого пространства будем обозначать:
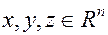.При этом 
.
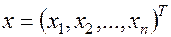Норму вектора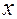 
будем обозначать так:
Нам требуется найти такой вектор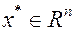 
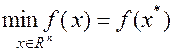(2.1)
Напомним, что задача поиска максимума функции сводится к задаче поиска минимума путем замены знака перед функцией на противоположный.
(2.2)
Заметим, что определения 1-5 в многомерном случае сохраняются, при этом вместо модуля понимается норма.(именно поэтому мы взяли такое обозначение нормы в многомерном случае).
Определение 8. Поверхностью уровня функции называется множество точек, в которых функция принимает постоянное значение,
Если n =2, то поверхность уровня является линией уровня в пространстве 
Определение 9. Градиентом непрерывно дифференцируемой функции в точке 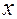называется вектор-столбец, элементами которого являются частные производные первого порядка, вычисленные в данной точке:
(2.3)
Градиент функции направлен по нормали к поверхности уровня, т.е. перпендикулярен к касательной плоскости, проведенной в точке 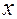, в сторону наибольшего возрастания функции в данной точке.
Определение 10. Матрицей Гессе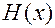 
дважды непрерывно дифференцируемой функции в точке 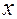называется матрица, элементами которой являются частные производные второго порядка, вычисленные в данной точке:
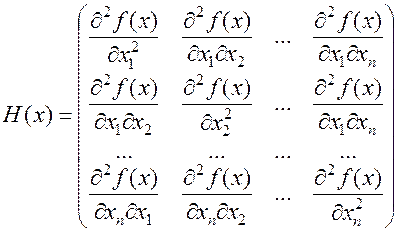(2.4)
Определение 11. Пусть функция определена в некоторой 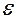окрестности точки 
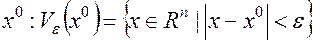. Эта функция называется дифференцируемой в точке 
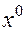, если ее можно представить в виде:
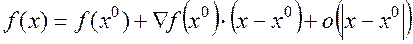(2.5)
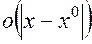- бесконечно малая величина, более высокого порядка, чем 
. Т.е.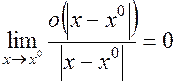 
.
Величина 
называется дифференциалом функции .
Определение 12. Пусть функция определена в некоторой 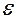окрестности точки 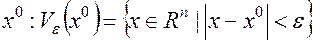. Говорят, что эта функция дважды дифференцируема в точке 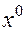, если наряду с 
существует симметрическая матрица Гессе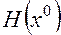 
размерности 
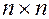, такая что ее можно представить в виде:
(2.6)
Определение 13. Квадратичная форма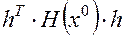 
а также матрица Гессе в точке 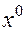,называется:
1, Положительно определенной, если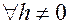 
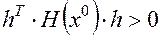
Обозначается 
2, Отрицательно определенной, если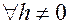 
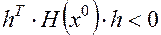
Обозначается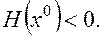 
3, Положительно полуопределенной, если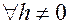 
Обозначается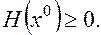 
4, Отрицательно полуопределенной, если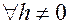 
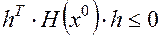
Обозначается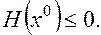 
5,Неопределенной, если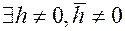 
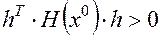, а
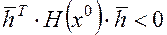или наоборот 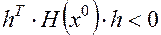а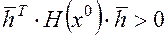 
6, Тождественно равной 0, если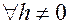 
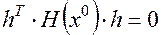
Обозначается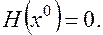 
Определение 14. Функция , определенная на выпуклом множестве 
называется выпуклой, если
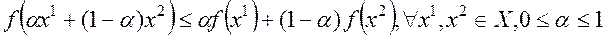Если неравенство строгое, то функция называется строго выпуклой.
Определение 15. Функция , определенная на выпуклом множестве называется сильно выпуклой с константой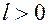 
, если
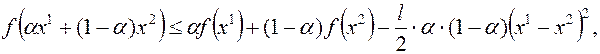
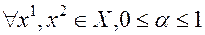
Если функция дважды непрерывно дифференцируема, то ее выпуклость можно определить по матрице Гессе.
Если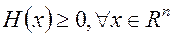 
то функция выпукла на всем пространстве
Если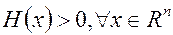 
то функция строго выпукла на всем пространстве
Если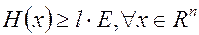 
то функция сильновыпукла на всем пространстве
2.2. Классический подход.
Теорема 6. Пусть 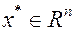является точкой локального экстремума функции на множестве и дважды дифференцируема в окрестности точки . Тогда
(2.7)
Точки, удовлетворяющие соотношению (2.7) называются стационарными.
Теорема 7. Пусть 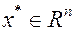является точкой локального минимума функции на множестве и дважды дифференцируема в окрестности точки . Тогда 
- матрица Гессе функции вычисленная в точке является положительно полуопределенной, т.е.
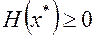
Теоремы 6 и 7 дают необходимые условия существования экстремума функции нескольких переменных. Теперь мы рассмотрим достаточные условия существования экстремума.
Теорема 8. Пусть дважды дифференцируема в окрестности точки . При этом и - матрица Гессе функции вычисленная в точке ,является положительно определенной, т.е.
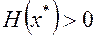. Тогда является точкой локального минимума.
Определение 14. Рассмотрим определитель матрицы Гессе в стационарной точке :
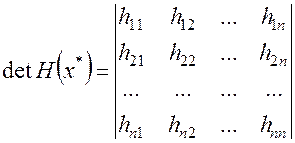(2.7)
Определители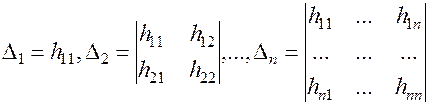 
называются угловыми минорами.