Способы задания ориентированного графа.

Пусть имеется граф, содержащий п вершин и т дуг.

1. Список дуг. Указываются: дуга, начальная вершина, конечная вершина.

2. Матрицей смежности графа называется квадратная матрица

R = [ r_ij ]порядка n 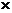n, где

3. Матрицей инцидентности графа (или матрицей инциденций для дуг графа) называется матрица S = [s _ij ] порядка п 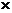т,

где

 

Пример.

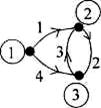Граф

Список дуг

дуга	нач. верш	кон. верш

 

 

 

 

 

Матрица инцидентности
Вершины	Дуги
j i
	-1		-1
		-1		-1

Матрица смежности

 

 

 

 

Начальные вершины	Конечные вершины
j i

 

Если есть петли, то в списке дуг начальная и конечная вершины совпадают. В матрице смежности 1 ставится в главной диагонали, а в матрицу инцидентности вводят дополнительное условие: если петля номер j исходит и входит в вершину i то s_ij равна любому числу (например 2), но не 0 и ±1.

Если к имеющемуся графу дорисовать дугу 5 в виде петли вершины 3, то в списке дуг появится строка 5 3 3, матрица смежности примет вид:

 

	1	2	3
1
2
3

а в матрице инцидентности появится еще один столбец

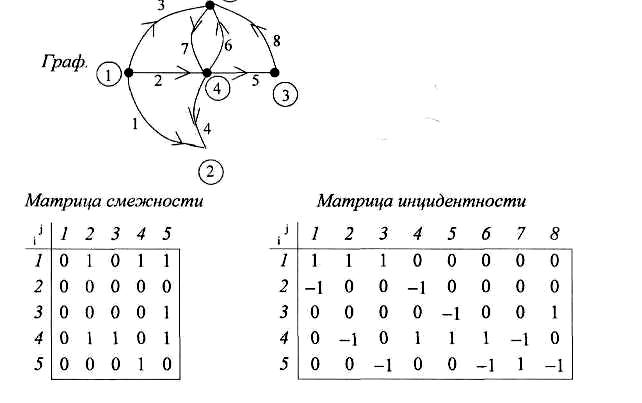
Иногда для графа с петлями матрицу инцидентности расчленяют на две: положительную и отрицательную. Еще один пример.

 

Дуги называются кратными, если выходят из одной вершины и входят в одну и ту же вершину

Графы и отношения

Ориентированному графу можно дать другое определение (трактовку). Пусть задано множество вершин X и способ отображения множества X само на себя, то есть задано отношение Г на множестве X. Тогда ориентированный граф – это пара множеств (Х,Г), состоящая из множества и заданных на нем отношений.

Графы могут использоваться как геометрическое представление бинарных отношений, заданных на множестве.

Отношение порядка: х<у, если существует путь из х в у (говорят: х предшествует у).

 

Отношение не строгого порядка обладает следующими свойствами:

1) рефлексивность х≤х - истина (хотя иногда это трактуется как наличие

петли

 

2. транзитивность х≤у и y≤z →x≤ z , это означает, что x,y,z - последовательно встречается на одном и том же пути.

3. антисимметричность: х≤у и х≥у → х ≡ у

это может означать, что х и у одна и та же вершина или,

что имеется контур на котором лежат х и у.

Отношение эквивалентности: х ≡ у - если х и у лежат на одном и том же контуре: рефлексивность х ≡ х; симметричность, если х ≡ у → у ≡ х; транзитивность, если х ≡ у и y ≡ z →x≡z.

Отношение строгого порядка: х <у путь из х в у есть, но пути из у в х нет: х <х - ложно (хотя это условие может трактоваться как отсутствие петель); несимметричность х<у → у<х ложно (выполняется, если нет контуров); транзитивность х <у, у <z→х <z.

 

III. Характеристики неориентированных графов

 

Неориентированные графы – графы, состоящие из вершин и соединяющих их ребер. Ребро – ненаправленный отрезок, соединяющий две вершины.

Маршрут – такая последовательность ребер, в которой соседние ребра имеют общую вершину.

Цепь – маршрут, в котором 1 ребро встречается только 1 раз.

Простая цепь – цепь, в которой 1 вершина встречается только 1 раз.

Циклический маршрут, цикл, простой цикл – это соответственно маршрут, цепь, простая цепь, у которой начальная и конечная точки совпадают.

То есть ребро, цепь, цикл неориентированного графа аналогичны понятиям дуга, путь, контур ориентированного графа (маршрут совпадает для неориентированного и ориентированного графа).

Вместо введенных определений возможны и другие подходы.

веденные определения:	Допустимые определения:
маршрут	маршрут	цепь
цепь	маршрут	простая цепь
простая цепь	цепь	элементарная цепь
замкнутый маршрут	замкнутый маршрут	цикл
цикл	замкнутый маршрут	простой цикл
простой цикл	цикл	элементарный цикл

Две вершины называются смежными, если существует соединяющие их ребер. Ребро инцидентное вершине, если соединяет эту вершину с другой. Петля – ребро, соединяющее одну и ту же вершину (хотя в неориентированных графах используется редко). Ребра, инцидентные одной и той же паре вершин называются кратными.

Кратные ребра ,петля .

Список ребер, матрицы смежности и инцидентности вводятся так же, как и для ориентированных графов, с той разницей, что не делается различий между заходящими в вершину и исходящими из нее отрезками.

Список ребер
Ребра:	Вершины
	1,2
	2,3
	1,3
	3,4

 

Матрица смежности i j                                                                       Матрица инцидентности i j

 

 

Понятие длины цепи вводится также как длина пути:

1) если ребра единичной длины, длина цепи равна сумме ребер,

2) если ребра произвольной длины, длина цепи равна сумме длин ребер.

В графе нет направлений, но после того как мы выбрали цепь, мы можем считать 1 вершину начальной и 1 вершину конечной и задать направление, то есть превратить цепь в путь. Точно также мы можем выбрать направление обхода цикла, тем самым, превратив его в контур.

Расстояние между вершинами x и y - длина кратчайшей простой цепи –d(x,y), то есть надо рассмотреть все возможные простые цепи между x и y и выбрать минимальную.

Условным радиусом относительно вершины х называется максимальное расстояние от вершины х до всех других вершин, то есть надо измерить расстояние до всех вершин, наибольшее расстояние будет условным радиусом.

Радиусом R графа G называется наименьший из условных радиусов, то есть надо вычислить условные радиусы относительно всех вершин, условный наименьший радиус будет радиус R графа G.

Диаметр D графа G - наибольшее расстояние между вершинами графа G, то есть надо измерить все расстояния между всеми точками, максимальное расстояние будет D, а соответствующая D цепь называется - диаметральная цепь, при этом R≤D≤2R

Пример:

(ребра единичной длины)

 

 

Точки (1,5), для которых условный радиус, совпадает с радиусом графа, называется - центр графа (центр может быть не единственный).

Степенью вершины (deg(x) или dx) называется число ребер инцидентных вершине. Пример

Теорема: пусть граф имеет n вершин и m ребер d_i - степень i^ой вершины, тогда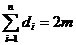

Каждое ребро добавляет по одной степени к каждой вершине, то есть по две степени к сумме степеней.

Следствие: в каждом графе число вершин нечетной степени четно.

 

Связанность графа

 

Две вершины связаны, если существует маршрут, соединяющие эти вершины. Граф связан (связанный), если любые его две вершины можно соединить маршрутом.

Если граф не связан, его можно разбить на подграфы, называемые компонентами связанности такие, что все вершины в подграфе связанны, а вершины различных подграфов не связанны. Из несвязанного графа можно сделать связанным, если добавить ребро, называемого мостом, или удалить уединенные вершины.

Понятие связанности относится и к ориентированным графам – при этом не обращают внимание на направление дуг. Ориентированный граф сильно связанный (связен), если для любых двух его вершин существует путь, идущий от одной вершины к другой.

сильно связанный

не сильно связанный

 

Эйлеровы графы

 

Цикл, включающий все ребра графа, называется эйлеровым циклом, а сам граф, в котором существует эйлеровый цикл, – эйлеровым графом (цикл –замкнутый маршрут, в котором 1 ребро встречается только 1 раз).

Эйлеров граф можно изобразить, не отрывая перо от бумаги, причем начальная и конечная точки совпадают. Задача о кенигсбергских мостах.

Можно ли по одному ряду обойти все мосты и вернуться на то же самое место? Нельзя.

 

С этой задачи традиционно считается начало теории графов, основу которой заложил Эйлер.

Теорема: граф эйлеров тогда и только тогда, когда он связан и степени
всех его вершин четные.

Цепь, включающая все ребра и вершины графа, называется эйлеровой (цепь – маршрут, в котором 1 ребро встречается 1 раз). В отличие от эйлерова цикла начальная и конечная вершина не совпадает.

Необходимое и достаточное условие существования в графе эйлеровой цепи: связанность графа и четность степеней всех его вершин, кроме начальной конечной.

Примеры:

 

Эйлеровы графы
Графы, включающие эйлерoвую цепь, но не цикл
Графы, не содержащие эйлеровых цепей и циклов

 

Гамильтоновы циклы и цепи

 

Простой цикл, включающий все вершины графа, называется гамильтоновым (все ребра в цикл могут не входить, главное, чтобы входили все вершины). Напоминание: простой цикл – цикл, в котором 1 вершина входит 1 раз. Граф, в котором имеется гамильтонов цикл, называется гамильтоновым.

Простая цепь, включающая все вершины графа, называется гамильтоновой (простая цепь – цепь, в которой 1 вершина входит 1 раз).

 

Граф, содержит гамильтонов цикл:

Граф, содержащий гамильтонову цепь, но не цикл:

 

Граф, не содержащий ни гамильтонову цепь, ни цикл:

 

Задача о лабиринте: Необходимое и достаточное условие выхода из лабиринта – чтобы граф был связанный, или что бы начальное и конечное положение принадлежали одной компоненте связанности. Для оптимального выхода из лабиринта необходимо двигаться по гамильтоновой цепи.

 

Цикломатическое число

 

Цикломатическим числом неориентированного графа G называется число v(G)=m–n+r, где m – число ребер, n – число вершин, r – число компонент связности. v(G) – показывает число независимых циклов (независимых контуров в электрической схеме), то есть минимальное число циклов, в которое входят все ребра.

Пример из электротехники.

т=3, п=2, r=1, v(G)=2, можно построить 2 независимых цикла, то есть достаточно двух циклов, что бы в эти циклы вошли все ребра.

 

Хроматическое число

 

Граф называется p – хроматическим, если его вершины можно раскрасить р различными цветами так, что никакие 2 смежные вершины не раскрашены одинаково.

Хроматическое число графа G: γ(G)=р.

Если γ(G)=2 – граф называется бихроматическим.

Необходимое и достаточное условие бихроматичности графа – отсутствие циклов нечетной длины.

бихроматические не бихроматические

Дерево

 

Конечный связанный неориентированный граф, не имеющий циклов, называется деревом.

Несвязанный неориентированный граф, не имеющий циклов, называется лесом, а каждая его компонента связанности – деревом.

Теорема: любые две вершины дерева связаны одной и только одной цепью. Вершина со степенью равной единице называется концевой (висячей) вершиной, а инцидентное ей ребро, называется концевым.

Теорема: каждое дерево имеет хотя бы 2 концевые вершины и 1 концевое ребро.

Иногда одну точку выделяют и называют корнем дерева.

 

 

Граф можно сделать ориентированным если идти от корня дерева к концевым вершинам (или наоборот). Такой граф называют ориентированным деревом. Путь от корня до концевой вершины называют ветвью. Вершину с максимальной степенью называют центром дерева.

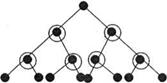
Центр может быть не единственным
(в этом случае говорят, что нет центра).

 

Примеры деревьев

1. Родословное дерево.

2. Структура предприятия.

3. Дерево целей, например,

S- национальная безопасность

S₁(готовн. к войне) S₂(демонстр. Силы)

и т.д.

4. Прогнозное дерево.

S причина

S₁ S₂ следствие

S₁₁ S₁₂ S₂₁ S₂₂ следствие следствия

5. Дерево задач.

S – освоение космоса

 

S – освоение Луны

S₁ – исследование S₂ – высадка человека

и т.д.

 

Изоморфизм графов

 

Геометрические изображения графов могут быть различными, но все основные характеристики совпадать. Такие графы называются изоморфными.

Точнее, графы изоморфны, если существует взаимнооднозначное соответствие между множеством вершин и ребер графа.

Изоморфные графы:

(А на самом деле из-за ошибки в рисунке один граф оказался не изоморфным. Найдите его!)

Неизоморфные графы: , хотя большинство характеристик совпадают.

У изоморфных графов, матрицы смежности и инцидентности, список ребер – совпадают. Перебрав все обозначения, рано или поздно получим одинаковые матрицы. А для неизоморфных графов матрицы не совпадут никогда.

Гиперграфы (сети, блок-схемы)

 

Множество вершин A={a₁,a₂,...a_n} и множество наборов, называемых полюсами, E={e₁,e₂,...e_m}, где ei = (a_i1...a_ij...), a_ij A, (то есть e – набор элементов из A), называется гиперграфом или сетью.

Обычно один из наборов е₀ называют внешним.

 

Пример.

A = (1,2,3,4,5,6)

e₀ = (1,5,6)

е₁ = (1,2,3,3,4)

е₂ = (2,4,5,6)

е₃ = (4,4,5)

Сеть, у которой e₀= 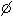, а для _i=1,2... е_i, – двухэлементное множество, является графом. При этом полюса e_i=(a_i1,a_i2) это ребра, связывающие две вершины a_i1 и a_i2, a_j – вершины графа.

 

IV. Задачи в теории графов

 

Построение графа кратчайшей длины

 

Дано: множество вершин х, построить связанный граф G=(x,u) такой, чтобы сумма длин ребер была минимальной ().

Пример практического использования: соединить города (населенные пункты) дорогами (или линиями электропередач), так что бы суммарная длина была минимальной. Такой граф G=(x,u) всегда дерево, т.к. если есть цикл, то одно ребро можно устранить.

Правило: Соединим две вершины самым коротким ребром, далее добавляем самое короткое ребро из оставшихся, но так, что бы не образовались циклы. Если несколько ребер одинаковые, то можно выбирать любое. Такое дерево называется экономическим, никакое другое дерево не может иметь меньшую длину, чем экономическое дерево.

 

Определение кратчайшего пути

 

Дано: неориентированный граф, найти цепь, соединяющую две вершины графа и имеющую минимальную длину. (Если две вершины назвать: начало и конец, то полученная цепь будет путем из одной точки в другую) (Дано G=(X,U), a,b x, найти цепь (путь): u_l...u_i...u_n, такую, что ).

а) Ребра единичной длины: конечной точке приписывая индекс 0, всем смежным - 1, далее всем смежным не имеющим индекса - 2 и т.д. Индекс вершины равен расстоянию до конечной точки. Надо двигаться в сторону уменьшения индексов.

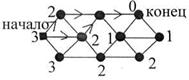
б) Ребра произвольной длины: конечной вершине приписывается индекс 0, смежным ,

где u_i - инцидентное конечной вершине ребро,

- её длина.

Далее всем смежным вершинам приписывается индекс , где
– индекс предыдущей вершины, u_i - ребро, соединяющее предыдущую вершину с последующей. Если вершина уже имела индекс, выбирается наименьший и так далее до начальной вершины (или до конца всех вершин). Индекс равен расстоянию до конечной точки.

Надо двигаться от начала до конца по тем ребрам, для которых длины ребер совпадают с разностью индексов вершин.

 

Транспортные сети

 

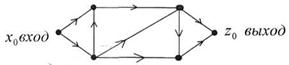
Транспортной сетью называется конечный ориентированный граф без петель, у которого:

1) существует 1 и только 1 вершина, называемая входом х₀, такая, что 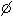(то есть дуги только выходят из х₀),

2) существует 1 и только 1 вершина, называемая выходом, такая, что 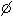(то есть дуги только входят в z),

3) каждой дуге соотнесено число c(u_i)>0, называемое пропускной способностью дуги.

Обычно стараются выбрать размерность c(u_i) так, что c(u_i) - целое.
Поток по дуге φ(u_i) -удовлетворяет условию 0≤φ(u_i)≤c(u_i), φ(u_i) – показывает количество вещества, проходящее по дуге, c(u_i) - максимальное количество вещества, которое может пропустить дуга. Если φ(u_i)=c(u_i), - дуга насыщена
(пропускает максимум, что может). Поток транспортной сети

, u_i – инцидентный x₀, u_j – инцидентны z₀.

Иногда дуге соотносится величина d(u_i) – стоимость единичного потока.

Решаются обычно две задачи:

1. По критерию максимального потока: Найти наибольший поток, который может пропустить транспортная сеть – φ(u_i) (при этом определяется также какой поток идет по каждой дуге φ(u_i)).

2. По критерию стоимости: По заданному потоку φ<φ⁰ необходимо найти такое распределение потока по дугам φ(u_i), что бы стоимость прохождения потока в сети была минимальной: .