Функция 
называется первообразной для функции 
в промежутке 
, если в любой точке этого промежутка ее производная равна :
, .
Отыскание первообразной функции по заданному дифференциалу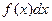 
есть действие, обратное дифференцированию, - интегрирование.
Совокупность первообразных для дифференциала 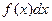называется неопределенным интегралом и обозначается символом 
.
, если 
.
Основные свойства неопределенного интеграла:
1. 
;
2. 
;
3. 
;
4. 
;
5. Если и 
- любая известная функция, имеющая непрерывную производную, то 
.
Основные формулы интегрирования
1. 
;
2. 
, 
, 
, 
;
3. 
;
4. 
, 
;
5. 
, 
;
6. 
, 
;
7. 
, 
;
8. 
, 
;
9. 
, 
;
10. 
, 
, 
;
11. 
, 
, 
;
12. 
;
13. 
.
Непосредственное интегрирование
Непосредственное интегрирование основано на прямом использовании табличных интегралов, свойств интегралов и применении элементарных тождественных преобразований.
Найти интегралы:
1. 
.
Решение:
Используя свойства 3 и 4 и формулы 2 и 1 получаем:
.
Ответ: 
.
2. 
.
Решение:
Так как 
, и 
, то
.
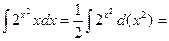
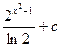Ответ: .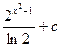
3. 
.
Решение:
Так как 
, и 
, то
.
Ответ: 
.
4. 
.
Решение:
Так как 
и 
, то
.
Ответ: 
.
5. 
.
Решение:
Выполним тождественные преобразования:
.
Ответ: 
.
6. 
.
Решение:
Ответ: 
.
Интегрирование методом замены переменной
Сущность этого метода заключается в преобразовании интеграла в интеграл 
.
Для нахождения интеграла заменяем переменную х новой переменной t с помощью подстановки 
. Дифференцируя это равенство, получим 
. Подставляя в подынтегральное выражение вместо х и dx их значения, выраженные через t и dt, имеем:
.
После нахождения интеграла возвращаемся к переменной х.
Найти интегралы:
1. 
.
Решение:
Данный интеграл окажется табличным, если под знаком дифференциала будет стоять аргумент 
.
Т.к. 
, то 
.
Ответ: 
.
2. 
.
Решение:
Поскольку 
, используем подстановку 
и 
, приводим выражение к табличному интегралу:
.
Ответ: 
.
В простейших случаях (подобных рассмотренным выше) введение новой переменной следует выполнить в уме, применяя следующие преобразования дифференциала 
:
,
,
,
,
и другие.
3. 
.
Решение:
Так как 
, то 
.
Разделив и умножив подынтегральное выражение на 
получим 
. Так как 
, получим 
.
Ответ: 
.
Интегрирование по частям
.
Вычисление 
сводится к вычислению 
, если последний окажется проще исходного.
За функцию u принимаются степенные, логарифмические, обратные тригонометрические функции, которые при дифференцировании упрощаются.
За 
принимаются 
, 
, 
, 
, 
, 
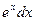и другие, интегрируя которые можно найти функцию 
.
Найти интегралы:
1. 
Ответ: 
.
2. 
Ответ: 
3. 
Ответ: 
Интегрирование тригонометрических функций
Рассмотрим следующие случаи:
1. При вычислении интегралов вида 
или 
используются формулы понижения степени:
, 
.
2. При вычислении интегралов вида 
или
от нечетной степени синуса или косинуса нужно отделить один множитель и ввести новую переменную, полагая 
в первом интеграле и 
во втором.
3. При вычислении интегралов вида 
, 
, 
применяются формулы:
;
;
.
Найти интегралы:
1. 
Ответ: 
.
2. 
Ответ: 
.
3. 
Ответ: 
.
Задание 4.
4.1 Найти интеграл:
1. 
; Ответ: 
.
2. 
; Ответ: 
.
3. 
; Ответ: 
.
4. 
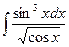; Ответ: 
.
5. 
; Ответ: 
.
6. 
; Ответ: 
.
7. 
; Ответ: 
.
8. 
; Ответ: 
.
9. 
; Ответ: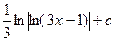 
.
10. 
; Ответ: 
.
11. 
; Ответ: 
.
12. 
; Ответ: 
.
13. 
; Ответ: 
.
14. 
; Ответ: 
.
15. 
; Ответ: 
.
16. 
; Ответ: 
.
17. 
; Ответ: 
.
18. 
; Ответ: 
.
19. 
; Ответ: 
.
20. 
; Ответ: 
.
21. 
; Ответ: 
.
22. 
; Ответ: 
.
23. 
; Ответ: 
.
24. 
; Ответ: 
.
25. 
; Ответ: 
.
26. 
; Ответ: 
.
27. 
; Ответ: 
.
28. 
; Ответ: 
.
29. 
; Ответ: 
.
30. 
; Ответ: 
.
31. 
; Ответ: 
.
32. 
; Ответ: 
.
33. 
; Ответ: 
.
34. 
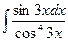; Ответ: 
.
35. 
; Ответ: 
.
36. 
; Ответ: 
.
37. 
; Ответ: 
.
38. 
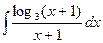; Ответ: 
.
39. 
; Ответ: 
.
40. 
; Ответ: 
.
41. 
; Ответ: 
.
42. 
; Ответ: 
.
43. 
; Ответ: 
.
44. 
; Ответ: 
.
45. 
; Ответ: 
.
46. 
; Ответ: 
.
47. 
; Ответ: 
.
48. 
; Ответ: 
.
49. 
; Ответ: 
.
50. 
; Ответ: 
.
51. 
; Ответ: 
.
52. 
; Ответ: 
.
53. 
; Ответ: 
.
54. 
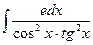; Ответ: 
.
55. 
; Ответ: 
.
56. 
; Ответ: 
.
57. 
; Ответ: 
.
58. 
; Ответ: 
.
59. 
; Ответ: 
.
60. 
; Ответ: 
.
61. 
; Ответ: 
.
62. 
; Ответ: 
.
63. 
; Ответ: 
.
64. 
; Ответ: 
.
65. 
; Ответ: 
.
66. 
; Ответ: 
.
67. 
; Ответ: 
.
68. 
; Ответ: 
.
69. 
; Ответ: 
.
70. 
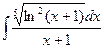; Ответ: 
.
71. 
; Ответ: 
.
72. 
; Ответ: 
.
73. 
; Ответ: 
.
74. 
; Ответ: 
.
75. 
; Ответ: 
.
76. 
; Ответ: 
.
77. 
; Ответ: 
.
78. 
; Ответ: 
.
79. 
; Ответ: 
.
80. 
; Ответ: 
.
81. 
; Ответ: 
.
82. 
; Ответ: 
.
83. 
; Ответ: 
.
84. 
; Ответ: 
.
85. 
; Ответ: 
.
86. 
; Ответ: 
.
87. 
; Ответ: 
.
88. 
; Ответ: 
.
89. 
. Ответ: 
.