Лекция № 5
Дифференциальные уравнения первого порядка
Многочисленные задачи естествознания, техники, механики, биологии, медицины и других отраслей знания сводятся к тому, что по заданным свойствам некоторого процесса или явления необходимо найти математическую модель самого процесса в виде формулы, связывающей переменные величины, то есть в виде функциональной зависимости.
При изучении таких задач используют дифференциальные уравнения.
Определение 1. Дифференциальным уравнением называют уравнение, связывающее между собой независимую переменную x, искомую функцию y и её производную или дифференциалы.
Определение 2. Дифференциальным уравнением называется уравнение, содержащее производные искомой функции или её дифференциалы.
Символически дифференциальное уравнение записывается так:
F(x, y, y,, y,,, …, y(n)) = 0 (1)
Определение 3. Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.
Определение 4. Порядком дифференциального уравнения называется порядок входящей в него старшей производной.
Например, y,, + 2y, + 5y = 0 – дифференциальное уравнение второго порядка.
Определение 5. Решением дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество.
Общим решением дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения. Так, общее решение дифференциального уравнения первого порядка содержит одну произвольную постоянную.
Частным решением дифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находятся при определённых начальных значениях аргумента и функции.
График частного решения дифференциального уравнения называется интегральной кривой. Общему решению дифференциального уравнения соответствует совокупность всех интегральных кривых.
Дифференциальным уравнением первого порядка называется уравнение, в которое входят производные не выше первого порядка.
Классификация дифференциальных уравнений и методы их решения приведены в таблице1.
Таблица № 1Дифференциальные уравнения
| Первого порядка Общий вид F(x, y, y,) = 0 или y, = f(x, y) | Второго порядка Общий вид F(x, y, y,, y,,) = 0 или y,, = f(x, y, y,) | |||||
| с разделёнными переменными | с разделяющимися переменными | линейные | частные случаи | |||
| Методы решения | y,, = f(x) | y,,= f(x,y,) | y,,=f(y,y,) | |||
| f(x)dx+φ(y)dy=0 или f(x)dx = –φ(y)dy – непосредствен ное интегрирование | y, = f(x)φ(y) или f1(x)φ1(y)dx = =f2(x)φ2(y)dy – разделение переменных | y,+P(x)y = Q(x) – подстановка y = uv, y, = u,v + v,u | Методы решения | |||
| y=∫(∫f(x)dx+C1)dx | y, = p, y,,= p, | y, = p,
y, = 
| ||||
Дифференциальные уравнения первого порядка с разделёнными переменными
Определение 6. Уравнение вида
f(x)dx + φ(y)dy = 0,
где f(x) и φ(y) – данные функции, называется уравнением с разделёнными переменными.
Это уравнение переписывают в виде:
f(x)dx = – φ(y)dy
и рассматривают как равенство двух дифференциалов. Решение таких уравнений выполняется непосредственным интегрированием.
Посмотрим на конкретных примерах.
Решить уравнения:
1) xdx + ydy = 0;
2) 
;
3) y ,= x;
4) Найти частные решения дифференциального уравнения: dy = (x2-1), если y = 4 при x = 1.
Решение.
1 xdx + ydy = 0,
ydy = – xdx,
∫ydy = – ∫xdx,
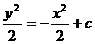– общее решение.
2 ,
,
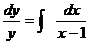lny = ln(x-1) + lnc,
lny = lnc(x-1),
y = c(x-1) – общее решение.
3 y, = x,
, следовательно,
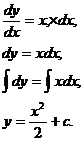
4 Найти частные решения дифференциального уравнения: dy = (x2-1), если y = 4 при x = 1.
То есть нашли сначала общее решение данного уравнения. Теперь начинаем использовать начальные условия, вместо y подставляем 4, а вместо x –1.
Задача нахождения частного решения по конкретным начальным условиям называется задачей Коши.