ЗАДАНИЕ НА ВЫПОЛНЕНИЕ РАБОТЫ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к выполнению контрольной работы по дисциплине

«Дискретная математика»

для студентов заочной формы обучения

направления 27.03.04-Управление в технических системах

 

 

Севастополь

 

 

УДК 681.5

 

Методические указания к выполнению контрольной работы по дисциплине

«Дискретная математика» для студентов заочной формы обучения направления 27.03.04-Упарвление в технических системах/Сост. А.И.Грушун, Т.А.Грушун.-Севастополь:Изд-во СевНТУ, 2015.- 7с.

 

 

В методических указаниях к выполнению контрольной работы содержатся индивидуальные задания, а также рассматриваются примеры их решения.

Указания предназначены для студентов заочной формы обучения направления подготовки 27.03.04-Управление в технических системах.

 

Указания рассмотрены и утверждены на заседании кафедры информатики и управления в технических системах (протокол №5 от 9 января 2015 г.).

 

Рецензент: Кожаев Е.А. канд. техн. наук, доцент.

 

 

СОДЕРЖАНИЕ

 

1.	Цель указаний
2.	Методические рекомендации
3.	Задание на выполнение работы
	Библиографический список

 

1. ЦЕЛЬ УКАЗАНИЙ

 

Обучение студентов методам решения задач прикладной дискретной математики, являющейся необходимым математическим базисом образования бакалавра в области управления в технических системах.

 

2. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

 

Методические указания содержат ряд задач Дискретной математики, которые позволяют закрепить приобретенные теоретические знания на конкретных примерах.

Индивидуальный вариант определяется конкретно в каждом задании. Также в каждом задании приводится пример решения типовой задачи.

Если решение типовой задачи вам непонятно, необходимо обратиться к соответствующему разделу теории и еще раз разобраться в теоретическом материале.

Если и после этого вы не можете решить задачу, необходимо обратиться за консультацией к ведущему преподавателю.

Теоретические сведения, необходимые для выполнения работы, приведены в [1, 2, 3, 4].

 

ЗАДАНИЕ НА ВЫПОЛНЕНИЕ РАБОТЫ

 

3.1 Представить число, заданное двумя последними цифрами номера Вашей зачетной книжки в 2, 8, 16 и 2-10 системах счисления, используя разложения на целые степени p, согласно формуле значимости.

 

Приведем пример для числа 146:

 

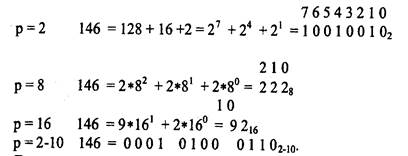3.2 Перевести число с помощью алгоритмов умножения и деления из 10-ной системы счисления в 8-ную, 2-ную и 16-ную. Исходное десятичное число формируется следующим образом: целая часть соответствует последним трем цифрам номера вашей зачетной книжки, дробная – последним двум цифрам номера вашей зачетной книжки.

 

Например, переведем в 8-ную систему число 314.159.

Переводом числа из р-ной системы счисления в q-ную назовем построение числа в q-ной системе, представляющего ту же величину, что и исходное число р-ной системы. Для выполнения этой операции число р-ной системы разбивают на целую часть и дробную и каждую часть переводят отдельно.

Целую часть делим на q, получая остаток и целое частное. Остаток используется для формирования значения очередной цифры целой части q-ного числа, начиная с младшей. Результат деления (частное) снова делят на q, получая очередные остаток и частное. Процесс продолжается до тех пор, пока очередное частное не станет равным нулю. Все операции осуществляются в р-ной системе счисления. Переводим целую часть заданного числа:

 

 

 

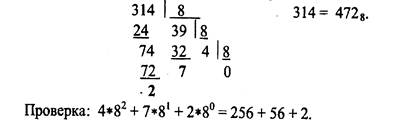Дробную часть числа переводим из р-ной в q-ную, умножая ее на основание q. Целая часть произведения используется для построения очередной цифры q-ного числа, начиная со старшей, с дробной частью проводим те же действия. Умножения дробной части проводим в исходной р-ной системе счисления. Преобразование дробной части заканчивается, когда достигается необходимая точность представления q-ного числа. Например, если в р-ной системе k разрядов дробной части, то в q-ной количество разрядов будет равно s, значение которого определяется по следующему неравенству: p^-k £ q^-s, т.е. s ³k*log_q p.

Для нашего примера: 10 ^-3 £ 2 ^-s, s ³ 4.

Переводим дробную часть заданного числа:

 

 

 

 

3.3 Просуммировать само с собой двоичное число, полученное в задании 3.1.

 

Так же как для 10-ной системы, арифметика двоичной системы определяется двумя таблицами – сложения и умножения:

 

 

¹0 – означает, что разряд суммы равен 0, однако возникает единица переноса в следующий разряд. При сложении очередных (i-х) разрядов двоичных чисел A и B участвуют значения a_i и b_i и перенос p_i-1 из предыдущего разряда. Формируются значения с_i разряда суммы и перенос p_i в следующий разряд.

Например:

 

 

 

Здесь А и В – восьмиразрядные двоичные слагаемые, С – восьмиразрядная двоичная сумма, Р – соответствующий двоичный вектор переносов между разрядами в процессе суммирования.

 

3.4Двоичное число, полученное в задании 3.2 контрольной работы, представить в форме с плавающей точкой.

Общая структура представления чисел с плавающей точкой имеет следующий вид: <знак порядка><порядок> <знак числа><мантисса>.

 

Примеры:

 

Двоичное число Форма плавающей точки

 

 

3.5 С помощью волнового алгоритма построить кратчайший путь для взвешенного графа, представленного на рисунке 1. Варианты весов дуг исследуемого графа представлены в таблице 1, номер варианта соответствует последней цифре номера зачетной книжки.

 

 

Рисунок 1 – Исследуемый граф

 

Таблица 1 - Варианты весов дуг исследуемого графа

Номер вари- анта	Вес дуги (х1,х2)	Вес дуги (х1,х3)	Вес дуги (х2,х3)	Вес дуги (х2,х4)	Вес дуги (х3,х4)	Вес дуги (х3,х5)	Вес дуги (х4,х5)	Вес дуги (х4,х6)	Вес дуги (х5,х6)

 

 

Рассмотрим формулировку алгоритма построения кратчайшего пути для взвешенного графа.

1. Начальная вершина х_н (х_н=х₁) получает вес V _н =0, ее номер вводится в массив М номеров вершин, изменивших вес. Остальные вершины х_i получают вес V _i =¥ и их номера не попадают в массив М.
2. Если массив М пуст, то выполняется пункт 3, иначе выбирается с исключением из него очередная вершина х_i и пересчитываются веса вершин, принадлежащих исходу G(х_i) вершины х_i:

 

" х_j Î G(х_i) (V _j =min(V _j, V _i + l_ij)).

 

Если вес V _j уменьшается, то номер j включается с приведением

подобных в М. Снова выполняется пункт 2. Вершины исхода G(х_i) для вершины х_i это вершины, в которые подходят дуги из вершины х_i.

1. Если вес V _k =¥, то делается вывод, что пути из вершины х_н к конечной вершине х_k нет. Иначе выполняется процедура выделения дуг, то есть выделяются те дуги и вершины х_j и х_i, разность весов которых равна l_ij. После выделения дуг строятся кратчайшие пути, длины которых равны V _k.

Рассмотрим пример. Задан взвешенный граф, представленный на рисунке 1. Веса дуг этого графа следующие: l₁₂ =1, l₁₃ =4, l₂₃ =2, l₂₄ =5, l₃₄ =2, l₃₅ =4, l₄₅ =1, l₄₆ =4, l₅₆ =2.

1. V _н = V ₁ =0, М={1}, V ₂ = V ₃ = V ₄ = V ₅ = V ₆ =¥.

2.

2.1. М¹0, i =1, M=0, G(х₁)={ х₂,х₃ };

V ₂ =min(¥, 0+1)=1, М={2};

V ₃ =min(¥, 0+4)=4, М={2,3}.

 

2.2. М¹0, i =2, M={3}, G(х₂)={ х₃,х₄ };

V ₃ =min(4, 1+2)=3, М={3};

V ₄ =min(¥, 1+5)=6, М={3,4}.

 

2.3. М¹0, i =3, M={4}, G(х₃)={ х₄,х₅ };

V ₄ =min(6, 3+2)=5, М={4};

V ₅ =min(¥, 3+4)=7, М={4,5}.

 

2.4. М¹0, i =4, M={5}, G(х₄)={ х₅,х₆ };

V ₅ =min(7, 5+1)=6, М={5};

V ₆ =min(¥, 5+4)=9, М={5,6}.

 

2.5. М¹0, i =5, M={6}, G(х₅)={ х₆ };

V ₆ =min(9, 6+2)=8, М={6}.

 

2.6. М¹0, i =6, M=0, G(х₆)=0.

 

2.7. М=0 и выполняется пункт 3.

 

1. Для иллюстрации выполнения пункта 3 изобразим граф с весами вершин, полученными в результате решения (рисунок 2). Вершины входа G^-1(х_i) для вершины х_i это вершины, из которых подходят дуги к вершине х_i.

 

 

 

 

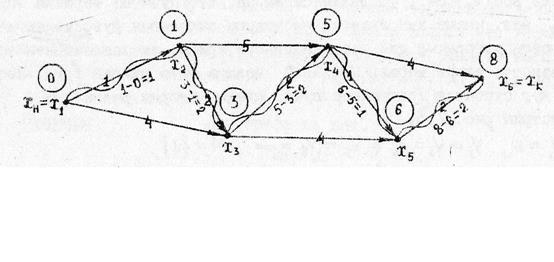
Рисунок 2 – Нахождение кратчайшего пути в графе

 

3.1. Начинаем с конечной вершины х_k=х₆: G^-1(х₆)= { х₄,х₅ };

(l₄₆ =4)¹(V ₆ - V ₄ =3), поэтому дуга (х₄,х₆) не выделяется;

(l₅₆ =2)=(V ₆ - V ₅ =2) и дуга (х₅,х₆) выделяется, одновременно выделяется вершина х₅.

 

3.2. Для выделенной вершины х₅: G^-1(х₅)= { х₃,х₄ };

(l₃₅ =4)¹(V ₅ - V ₃ =3), дуга (х₃,х₅) не выделяется;

(l₄₅ =1)=(V ₅ - V ₄ =1), выделяется дуга (х₄,х₅) и вершина х₄.

 

3.3. Для выделенной вершины х₄: G^-1(х₄)= { х₂,х₃ };

(l₂₄ =5)¹(V ₄ - V ₂ =4), дуга (х₂,х₄) не выделяется;

(l₃₄ =2)=(V ₄ - V ₃ =2), выделяется дуга (х₃,х₄) и вершина х₃.

 

3.4. Для выделенной вершины х₃: G^-1(х₃)= { х₁,х₂ };

(l₁₃ =4)¹(V ₃ - V ₁ =3), дуга (х₁,х₃) не выделяется;

(l₂₃ =2)=(V ₃ - V ₂ =2), выделяется дуга (х₂,х₃) и вершина х₂.

 

3.5. Для выделенной вершины х₂: G^-1(х₂)= { х₁ };

(l₁₂ =1)¹(V ₂ - V ₁ =1), выделяется дуга (х₁,х₃) не выделяется;

(l₂₃ =2)=(V ₃ - V ₂ =2), выделяется дуга (х₂,х₁).

Построен кратчайший путь длиной 8:

(х_н=х₁,х₂)(х₂,х₃)(х₃,х₄)(х₄,х₅)(х₅,х₆ = х_k).