ПЕНЗЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
КАФЕДРА "КОМПЬЮТЕРНЫЕ ТЕХНОЛОГИИ"
ЧИСЛЕННЫЕ МЕТОДЫЛИНЕЙНОЙ АЛГЕБРЫ.
РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ
Отчет
о выполнении индивидуального задания
по дисциплине: "Численные методы"
Выполнил: студент гр. ……… Иванов И. И.
Проверил: д.т.н., профессор Горбаченко В. И.
Пенза, 2013
1. Цель работы: разработать программу, позволяющую находить решение системы уравнений методами простой итерации и Ньютона.
Задание
Номер варианта ….. Методами простой итерации и Ньютона решить систему уравнений
Исследовать влияние начального приближения на сходимость итерационного процесса. Сравнить методы.
Анализ задания
Необходимо преобразовать уравнения системы для решения методами простой итерации и Ньютона, разработать соответствующие программы, исследовать влияние начального приближения и сравнить методы.
Описание метода решения
Метод простой итерации
Пусть требуется решить систему нелинейных уравнений [1]
[GVI1]
где 
— нелинейные вещественные функции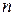 
вещественных переменных 
.
Систему можно заменить одним уравнением
,
где
.
Система преобразуется к виду:
,
или в компактном виде:
.
Для решения такой системы используется рекуррентное соотношение:
,
или в развернутом виде
Если начать процесс построения последовательности 
с некоторого вектора 
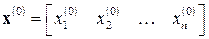и продолжить вычислительный процесс по формуле, то данная последовательность со скоростью геометрической последовательности будет приближаться к истинному значению вектора решения системы. Вычисления прекращаются только тогда, когда 
, где 
— произвольная норма, 
– малая величина.
Для реализации метода простой итерации преобразуем систему к виду:
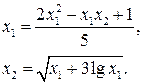
Используя формулу находим решение системы.
Краткое описание метода Ньютона (метода касательных
Пусть требуется решить систему нелинейных уравнений. Метод Ньютона состоит в построении итерационной последовательности [1]
.
Вектор поправки 
формируется в результате решения системы линейных алгебраических уравнений
,
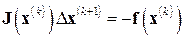где
— матрица Якоби (Якобиан) [2].
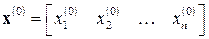Если начать процесс построения последовательности с некоторого вектора и продолжить вычислительный процесс по формуле, то данная последовательность со скоростью геометрической последовательности будет приближаться к истинному значению вектора решения системы. Вычисления прекращаются только тогда, когда , где — произвольная норма, – малая величина. Метод Ньютона является более точным в сравнении с методом простых итераций. Начальное приближение в методе Ньютона следует задавать как можно ближе к истинному значению решения системы, т.к. может произойти расхождение процесса приближений.
Для решения системы находим Якобиан
.
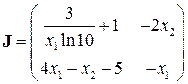Найдем обратную матрицу[GVI2]
,
где 
— определитель 
.
С учетом полученных выражений находим искомое решение системы по формуле.
Описание программы
Начальное приближение найдем графически путем построения графиков функций с помощью m‑файла grafiki.(Приложение А). По полученному графику (рис. 1) определяем начальное приближение: 
.
Программа (дать название программы) предназначена для нахождения решение системы уравнений методами простой итерации и Ньютона (приложение).
Описать структуру программы: главная программа, вызываемые функции. Описать каждую программу: имя, назначение, входные и выходные данные, что запрашивает программа, что выдает, возможные реакции программы на разные ситуации.
Рис. 1. Поиск начального приближения графически
Описание применения
Описать, как работать с программой.
Анализ результатов
Привести и пояснить результаты из командного окна, графики (большие таблицы вынести в приложения).
Результаты решения показывают, что для решения системы методом простой итерации необходимо 17 итераций, в то время как для метода Ньютона достаточно лишь трех итераций и метод Ньютона обеспечивает большую точность.
В данном задании надо было исследовать влияние начального приближения: в виде графиков или таблиц показать, сколько итераций потребовалось в разных методах при разных начальных приближениях.
Заключение
В процессе выполнения работы была создана программа нахождения методом простой итерации методом Ньютона решение системы уравнений, проведено исследование …… методов, показавшее …….
Список использованных источников
1. Вержбицкий В. М. Численные методы (линейная алгебра и нелинейные уравнения), 2-е изд., испр. — М.: ООО "Издательский дом "ОНИКС 21 век", 2005. — 432 с.
2. Шевцов Г. С., Крюкова О. Г., Мызникова Б. И. Численные методы линейной алгебры. — М.: Финансы и статистика: ИНФРА‑М, 2008. — 480 с.
ПРИЛОЖЕНИЯ
Приложение А <Название>
x=[0.1:0.001:5];
y1=(2*x.^2-5*x+1)./x;
y2=sqrt(x+3*log10(x));
y3=-sqrt(x+3*log10(x));
plot(x,y1,x,y2,'-',x,y3,'-')
ylabel('y')
xlabel('x')
legend('y=(2*x^2-5*x+1)/x','y=+-sqrt(x+3*log10(x))',0)
grid on
Приложение Б <Название>
% Метод простой итерации
x0=[1.5;-1.5]; % вектор начальных приближений
y=x0; % первоначальный вектор решений
h=0.001; % точность вычислений
k=1; % число, показывающее на сколько отличаются
% последующее значение от предыдущего в итерационном процессе
i=0; % счетчик итераций
while k > h % цикл выполнения итераций
i=i+1;
x(2,1)=sqrt(y(1,1)+3*log10(y(1,1))); % 2-ое уравнение
x(1,1)=sqrt((5*y(1,1)+y(1,1)*y(2,1)-1)/2); % 1-ое уравнение
s=x-y; % вектор разности
k=abs(s(1,1)-s(2,1));
y=x; % присвоение предыдущему значению последнего значения
end
y % решение системы, полученное с помощью метода простых итераций
i % число итераций
% Метод Ньютона решения сиcтемы нелинейных уравнений
y1=x0;
h=0.001;
m=1;
n=1;
i=0; % счетчик итераций
while m > h %цикл выполнения метода Ньютона
i=i+1;
f(1,1)=y1(1,1)+3*log10(y1(1,1))-y1(2,1)^2; % 1-ая функция
f(2,1)=2*y1(1,1)^2-y1(1,1)*y1(2,1)-5*y1(1,1)+1; % 2-ая функция
w(1,1)=3/(y1(1,1)*log(10))+1;%элементы якобиана
w(1,2)=-2*y1(2,1); %элементы якобиана
w(2,1)=4*y1(1,1)-y1(2,1)-5;%элементы якобиана
w(2,2)=-y1(1,1);%элементы якобиана
D=w(1,1)*w(2,2)-w(1,2)*w(2,1); % определитель якобиана
% элементы приведенной матрицы якобиана
w1(1,1)=w(2,2);
w1(1,2)=-w(1,2);
w1(2,1)=-w(2,1);
w1(2,2)=w(1,1);
w11=w1/D; %вычисление матрицы якобиана
x1=y1-w11*f; %вычисление вектора последующей итерации
s1=x1-y1; % вектор разности
m=abs(s1(1,1)-s1(2,1));
y1=x1;
end
y1 % вектор-решение, полученный с помощью метода Ньютона
i % число итераций
% Проверка решений
% по методу простых итераций
rit=fmsys(y)
% по методу Ньютона
rnew=fmsys(y1)
Приложение В Б <Название>
function g=fmsys(x)
g(1,1)=2*x(1,1)^2-x(1,1)*x(2,1)-5*x(1,1)+1; % 1-ая функция
g(2,1)=x(1,1)+3*log10(x(1,1))-x(2,1)^2; % 2-ая функция
[GVI1]
Нумеруются только те формулы, на которые имеются ссылки.
При использовании MathType применять автоматическую нумерацию формул
[GVI2]Надо использовать один из методов решения СЛАУ