Транспортная задача
Рассмотрим простейшую постановку транспортной задачи. В m пунктах отправления А1, А2,..., Ат находится однородный груз, в количествах a1, a2,..., aт единиц (ед.) (например, тонн) соответственно. Потребность в этом грузе в п пунктах назначения В1, В 2,..., Вт составляет соответственно b1, b2,..., bт ед. груза. Стоимость перевозки ед. груза (удельная стоимость) из пункта Аi в пункт Вj (короче, из Аi в Bj) равна cij, i = 1, 2,..., т, j = 1, 2,..., n. Все эти данные можно свести в табл. 1, называемую матрицей перевозок, разграфив ее для удобства на клетки.
Таблица 1
| ai / bj | b1 | b2 | … | bn |
| a1 | c11 | c12 | … | c1n |
| a2 | c21 | c22 | … | c2n |
| … | … | … | … | … |
| am | cm1 | cm2 | … | cmn |
Можно считать, что сумма a запасов в пунктах отправления равна суммарным потребностям b в пунктах назначения, т.е.
 . (1)
. (1)
Такая модель транспортной задачи называется закрытой. Если условие (1) не выполняется, т.е. модель открытая, то в случае, когда а > b, вводят фиктивный пункт назначения Bn+1, полагая
bn+1 = a-b, ci,n+1 = 0, i=1, 2,..., m.
Если, наоборот, а < b, то вводят фиктивный пункт отправления Am+1, полагая
am+1 = b-a, cm+1,j = 0, j=1, 2,..., n.
Пусть xij — неизвестный пока объем груза, который по плану перевозок следует доставить из Аi в Bj, i = 1, 2,..., т, j = 1, 2,..., n. Занесем неизвестные xij в табл. 1 и приступим к составлению ограничений. Возьмем какой-нибудь пункт отправления, например Аi. Весь груз из него должен быть вывезен (это следствие того, что модель закрытая), поэтому сумма неизвестных в i -ой строке табл. 1 должна равняться ai, т.е.
xi1 + xi2 +... + xin = ai, i = 1, 2,..., m.
Таким образом, получим систему линейных уравнении (2) для пунктов отправления. Аналогично, сумма неизвестных, стоящих в j -ом столбце табл. 1, должна равняться bj, т.е.
x1j + x2j +... + xmj = bj, j = 1, 2,..., n.
В результате получим систему линейных уравнении (3) для пунктов назначения. Естественно, неизвестные в этих системах должны быть неотрицательны.
x11 + x12 +... + x1n = a1,
x21 + x22 +... + x2n = a2, (2)
…
xm1 + xm2 +... + xmn = am;
x11 + x21 +... + xm1 = b1,
x12 + x22 +... + xm2 = b2, (3)
…
x1n + x2n +... + xmn = bn.
Предполагая, что стоимость перевозок пропорциональна количеству перевозимого груза, общую стоимость перевозок можно выразить формулой
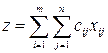 . (4)
. (4)
Итак, для решения поставленной задачи требуется среди неотрицательных решений системы линейных уравнений (2)-(3) найти решение, дающееминимум форме z (4).
Система линейных уравнений (2)-(3), состоит из (т + n) уравнений с т • n неизвестными, причем эта система линейно зависима, так как в силу условия (1) сумма первых m уравнений (подсистема (2)) совпадает с суммой остальных n уравнений (подсистема (3)). Это означает, что ранг системы (2)-(3) меньше, чем (m+n). Можно показать, что он равен m+n- 1, следовательно, базис системы уравнений (2)-(3) содержит m + n - 1 неизвестных.
Непосредственное применение симплекс-метода к решению сформулированной задачи ЛП затруднительно из-за большого числа переменных. Поэтому разработаны его модификации, учитывающие специфику транспортной задачи. Ниже будет рассмотрен распределительный метод решения транспортной задачи. Все необходимые вычисления по этому методу можно оформить с помощью матрицы перевозок.
Решение транспортной задачи начинается с нахождения какого-либо допустимого базисного решения.
Формирование начального плана методом северо-западного угла
Самым простым способом отыскания исходного базисного решения является правило северо-западного угла. Такое название объясняется тем, что распределение груза в матрице перевозок идет слева направо и сверху вниз, что соответствует движению на географической карте с началом на северо-западе. Суть этого способа видна из следующего примера.
Пример 1. Исходные данные транспортной задачи сведены в табл. 2. Найти базисное решение по правилу северо-западного угла.
Таблица 2.
| ai \ bj | b1=25 | b2=10 | b3=35 | b4=5 | b5=35 |
| a1 =20 | |||||
| a2 =30 | |||||
| a3 =45 | |||||
| a4 =15 |
Схема распределения груза по правилу северо-западного угла состоит в следующем. Попытаемся удовлетворить потребности пункта назначения В1 в 25 ед. груза (1-ая колонка плана перевозок xij)
За счет пункта отправления А1 можно удовлетворить только 20 ед., т.е. полагаем x11 = 20. Недостающие 5 ед. для пункта В1 берем из пункта А2, т.е. х21 = 5. После этого план перевозок xij примет вид
| ai \ bj | b1=25 | b2=10 | b3=35 | b4=5 | b5=35 | Остаток ai |
| a1 =20 | ||||||
| a2 =30 | ||||||
| a3 =45 | ||||||
| a4 =15 | ||||||
| Остаток bj |
В нижней строке и правом столбце указываем остаток нераспределенного груза. В строке для А1 и в столбце для В1 остаток равен нулю, т.е груз полностью распределен.
За счет А2, где осталось 25 ед., удовлетворяем также В2, полагая x22 = 10. В столбце для В2 получаем остаток, равный нулю. Поэтому оставшиеся в А2 15 ед. отправляем в В3. Продолжая аналогичным образом, получим следующий план перевозок (в числителе клетки показаны значения cij, а в знаменателе – xij):
Таблица 3.
| ai \ bj | b1=25 | b2=10 | b3=35 | b4=5 | B5=35 |
| a1 =20 | 5 / 20 | 6 / 0 | 2 / 0 | 3 / 0 | 1 / 0 |
| a2 =30 | 3 / 5 | 7 / 10 | 8 / 15 | 6 / 0 | 8 / 0 |
| a3 =45 | 9 / 0 | 8 / 0 | 1 / 20 | 4 / 5 | 3 / 20 |
| a4 =15 | 9 / 0 | 3 / 0 | 6 / 0 | 10 / 0 | 7 / 15 |
Ненулевыми оказалось m+n -1= 4+5-1=8 клеток. Они соответствуют неизвестным
x11, x21, x22, x23, x33, x34, x35, x45. (5)
Можно показать, что систему уравнении вида (2)-(3) для данной задачи можно разрешить относительно указанных неизвестных (5), т.е. эти неизвестные образуют базис, а решение, полученное в табл. 3, является базисным для базиса (5). Клетки в матрице перевозок, отвечающие базисным неизвестным, принято называть базисными, а остальные - свободными. Для того чтобы базисные клетки отличить от свободных, будем выделять их более жирным шрифтом, помещая в знаменателе значение базисного неизвестного в базисном решении. В свободных клетках будем помещать в знаменателе нули.
Полученный план перевозок имеет стоимость
Z = 5*20+3*5+7*10+8*15+1*20+4*5+3*20+7*15 = 100+15+70+120+20+20+60+105 = 510
Формирование начального плана методом наименьшей стоимости
Распределение груза по правилу северо-западного угла производится в порядке номеров пунктов отправления и назначения и совершенно не учитывает удельные стоимости с,, перевозок. При распределении груза по методу наименьшей стоимости в первую очередь заполняется клетка с наименьшей удельной стоимостью, причем, если таких клеток несколько, то предпочтение отдается той, где может быть помещено большее количество груза.
Рассмотрим метод на исходных данных примера 1. Укажем в знаменателе клеток – порядковый номер в упорядоченной по возрастанию последовательности cij. При одинаковых значениях cij приоритет устанавливаем по убыванию max(ai, bj) (значение приведено в скобках в числителе):
Таблица 4.
| ai \ bj | b1=25 | b2=10 | b3=35 | B4=5 | B5=35 |
| a1 =20 | 5(25) / 9 | 6(20) / 12 | 2(35) / 3 | 3(20) / 6 | 1(35) / 2 |
| a2 =30 | 3(30) / 5 | 7(30) / 14 | 8(35) / 16 | 6(30) / 11 | 8(35) / 17 |
| a3 =45 | 9(45) / 18 | 8(45) / 15 | 1(45) / 1 | 4(45) / 8 | 3(45) / 4 |
| a4 =15 | 9(25) / 19 | 3(15) / 7 | 6(35) / 10 | 10(15) / 20 | 7(35) / 13 |
Начинаем распределение с элемента х33 =35 (т.к. В3 может принять только такое количество груза), затем x15 = 20 и заносим в табл. 5. Так как запасы пункта A1 исчерпаны, то 1-я строка исключается из дальнейшего рассмотрения, так же как в 3-й столбец, поскольку потребности В3 также удовлетворены. В табл. 5 они для дальнейшего удобства отмечены крестиками в самом правом столбце и самой нижней строке.
Таблица 5.
| ai \ bj | b1=25 | b2=10 | b3=35 | B4=5 | B5=35 | |
| a1 =20 | 5 / 0 | 6 / 0 | 2 / 0 | 3 / 0 | 1 / 20 | Х |
| a2 =30 | 3 / 0 | 7 / 0 | 8 / 0 | 6 / 0 | 8 / 0 | |
| a3 =45 | 9 / 0 | 8 / 0 | 1 / 35 | 4 / 0 | 3 / 0 | |
| a4 =15 | 9 / 0 | 3 / 0 | 6 / 0 | 10 / 0 | 7 / 0 | |
| Х |
В оставшихся клетках табл. 4 наименьший порядковый номер в знаменателе равен 4 в клетке (3,5). Для пункта В5 остаток составляет 15 ед. груза, а в A3 – 10. Присваиваем х35 =10 и закрываем для распределения пункт A3. Из оставшихся клеток табл. 4 наименьший порядковый номер в знаменателе равен 5 в клетке (2,1). Присваиваем х21 =25 и закрываем для распределения пункт В1. Полученный план представлен в табл. 6.
Таблица 5.
| ai \ bj | b1=25 | b2=10 | b3=35 | B4=5 | B5=35 | |
| a1 =20 | 5 / 0 | 6 / 0 | 2 / 0 | 3 / 0 | 1 / 20 | Х |
| a2 =30 | 3 / 25 | 7 / 0 | 8 / 0 | 6 / 0 | 8 / 0 | |
| a3 =45 | 9 / 0 | 8 / 0 | 1 / 35 | 4 / 0 | 3 / 10 | Х |
| a4 =15 | 9 / 0 | 3 / 0 | 6 / 0 | 10 / 0 | 7 / 0 | |
| Х | Х |
В оставшихся клетках табл. 4 наименьший порядковый номер в знаменателе равен 7 в клетке (4,2). Для пункта В2 остаток составляет 10 ед. груза. Присваиваем х42 =10 и закрываем для распределения пункт В2. Далее присваиваем х24 =5 и закрываем для распределения пункт В4 и A2.
Таблица 6.
| ai \ bj | b1=25 | b2=10 | b3=35 | B4=5 | B5=35 | |
| a1 =20 | 5 / 0 | 6 / 0 | 2 / 0 | 3 / 0 | 1 / 20 | Х |
| a2 =30 | 3 / 25 | 7 / 0 | 8 / 0 | 6 / 5 | 8 / 0 | Х |
| a3 =45 | 9 / 0 | 8 / 0 | 1 / 35 | 4 / 0 | 3 / 10 | Х |
| a4 =15 | 9 / 0 | 3 / 10 | 6 / 0 | 10 / 0 | 7 / 0 | |
| Х | Х | Х | Х |
Единственная незакрытая клетка (4,5). Присваиваем ей х45 =5. Окончательный план приведен в табл. 7.
Таблица 7.
| ai \ bj | b1=25 | b2=10 | b3=35 | B4=5 | B5=35 | |
| a1 =20 | 5 / 0 | 6 / 0 | 2 / 0 | 3 / 0 | 1 / 20 | Х |
| a2 =30 | 3 / 25 | 7 / 0 | 8 / 0 | 6 / 5 | 8 / 0 | Х |
| a3 =45 | 9 / 0 | 8 / 0 | 1 / 35 | 4 / 0 | 3 / 10 | Х |
| a4 =15 | 9 / 0 | 3 / 10 | 6 / 0 | 10 / 0 | 7 / 5 | Х |
| Х | Х | Х | Х | Х |
Распределение груза закончено. Подученное в табл. 7 решение оказалось вырожденным, так как содержит 7 ненулевых значений неизвестных вместо нужных 8 = m+n –1=4+5-1. Дня того чтобы иметь 8 базисных клеток, нужно в одну из незаполненных клеток (но не любую), например, в клетку с индексами (3, 4), поместить нуль. Получим табл. 8. В ней.8 базисных клеток для наглядности отмечены цветом. Значения базисных неизвестных в базисном решении равны x15 = 20, x21 = 25, x24 =5, x33 = 35, x34 = 0, x35 = 10, x42 = 10, x45 = 5.
Таблица 8.
| ai \ bj | b1=25 | b2=10 | b3=35 | b4=5 | B5=35 |
| a1 =20 | 5 / 0 | 6 / 0 | 2 / 0 | 3 / 0 | 1 / 20 |
| a2 =30 | 3 / 25 | 7 / 0 | 8 / 0 | 6 / 5 | 8 / 0 |
| a3 =45 | 9 / 0 | 8 / 0 | 1 / 35 | 4 / 0 | 3 / 10 |
| a4 =15 | 9 / 0 | 3 / 10 | 6 / 0 | 10 / 0 | 7 / 5 |
Стоимость перевозок
Z = 1*20+3*25+6*5+1*35+4*0+3*10+3*10+7*5 = 20+75+30+35+30+30+35 = 255,
Что в два раза меньше, чем для плана, полученного методом северо-западного угла.
Распределительный метод
Решая транспортную задачу распределительным методом, переходят от одного базисного решения к другому таким образом, что стоимость перевозок уменьшается (не увеличивается). Такой переход осуществляется с помощью цикла пересчета свободной клетки. Циклом в матрице перевозок называется замкнутая ломаная линия, составленная из горизонтальных и вертикальных отрезков, вершины которой находятся в клетках таблицы,
 | 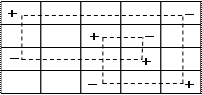 | ||
Рис. 1
Приведем некоторые свойства циклов.
Свойство 1. Число вершин в цикле четно.
Припишем каждой вершине цикла знак "+" или "–" таким образом,.чтобы две соседние вершины имели разные знаки. Такой цикл назовем означенным. Будем для краткости называть клетку, в которую попала вершина означенного цикла со знаком "+", положительной, а клетку с вершиной, помеченной знаком "–" — отрицательной.
Свойство 2. В любой строке (столбце) матрицы перевозок, где находятся вершины означенного цикла, число положительных клеток равно числу отрицательных клеток.
Свойство 3. Если в матрице перевозок размеров т на п, т ³ 2, п ³ 2 указать произвольным образом (m + n) клеток, то существует цикл, все вершины которого находятся необязательно во всех указанных клетках.
Пусть дано некоторое решение системы уравнений (2)-(3). Внесем значения неизвестных, которые они принимают в этом решении, в соответствующие клетки матрицы перевозок. Построим в матрице перевозок некоторый цикл, означим его. Затем значения неизвестных, стоящие в положительных клетках, увеличим на некоторое число x0, а значения неизвестных, стоящие в отрицательных клетках, уменьшим на то же число x0. Такое преобразование матрицы перевозок называется сдвигом по данному циклу на число x0.
Теорема 1. Сдвиг по циклу на некоторое число x0 , отличное от нуля, переводит одно решение системы уравнений (2)-(3) в некоторое другое решение этой системы.
Действительно, по свойству 2 циклов сумма значений неизвестных в любой строке (столбце) матрицы перевозок, где находятся вершины цикла, остается неизменной при сдвиге по циклу.
Пусть найдено некоторое базисное решение системы уравнений (2)-(3). Ему соответствует стоимость перевозок, определяемая формулой (4). Впишем значения базисных неизвестных в соответствующие клетки матрицы перевозок, отметив их цветом.
Теорема 2. Не существует цикла, все вершины которого находятся в базисных клетках.
Предположим обратное: пусть такой цикл существует. Означим его и произведем сдвиг по этому циклу на некоторое число x0. Тогда базисные неизвестные изменят свои значения, т.е. по теореме 1 получим новое решение системы (2)-(3), в то время как свободные неизвестные не изменят свои значения (они по-прежнему равны нулю), что невозможно.
Теорема 3. Для каждой свободной клетки существует, и притом единственный, цикл, одна вершина которого находится в данной свободной клетке, а все остальные — в базисных, необязательно во всех.
Действительно, возьмем произвольную свободную клетку. Число базисных клеток вместе с взятой свободной равно (m+n). По свойству 3 циклов найдется цикл, все вершины которого находятся в этих (т +п) клетках, необязательно во всех, но по теореме 2 одна вершина обязательно попадет в данную свободную клетку. Покажем, что этот цикл единственный. Предположим, что нашелся другой цикл, одна вершина которого находится в данной свободной клетке, а остальные — в базисных. Тогда означим оба цикла так, чтобы их общая вершина в свободной клетке имела бы знак "+", и произведем по одному из циклов сдвиг на число x0 ¹0, – а по другому циклу — на число (–x0). В результате базисные неизвестные в тех клетках, где вершины циклов не совпадают, изменят свои значения, в то время как свободные неизвестные не изменят свои значения (они по-прежнему равны нулю), что невозможно.
Цикл, существование и единственность которого для данной свободной клетки следует из теоремы 3, будем всегда означивать так, чтобы свободная клетка была положительной. Он называется циклом пересчета данной свободной клетки.
Пусть в матрицу перевозок внесено некоторое допустимое базисное решение. Возьмем произвольную свободную клетку, например с индексами (i, j) (короче, клетку (i, j)), и построим для нее цикл пересчета, см. рис. 2. Осуществим сдвиг по циклу на некоторое число x0. Это приведет по теореме 1 к новому решению системы уравнений (2)-(3) и изменению стоимости перевозок, равному
Dz = cijx0 – cikx0 + clkx0 – … + cstx0 – csjx0 = S (c+ij – c–ij) x0 (5)
В формуле (5) через c+ij и c–ij символически обозначены удельные стоимости, находящиеся соответственно в положительных и отрицательных базисных клетках. Индексы i и j указывают на то, что в этих клетках находятся вершины цикла пересчета свободной клетки (i, j). Величина
d ij = S (c+ij – c–ij) = cij – cik + clk – … + cst – csj (6)
называется оценкой свободной клетки (i, j) для данного базисного решения. Она не зависит от величины сдвига x0. Экономический смысл оценки d ij свободной клетки (i, j) состоит в том, что она равна изменению стоимости перевозок при сдвиге по циклу пересчета свободной клетки (i, j) на единицу груза.
Таблица 9.
| ai \ bj | b1=25 | b2=10 | b3=35 | b4=5 | B5=35 | ||
 a1 =20 a1 =20
| 5 / 0 | 6 / 0 | 2 / 0 | 3 / 0 | 1 / 20 | ||
| a2 =30 | 3 / 25 | 7 / 0 | 8 / 0 | 6 / 5 | 8 / 0 | ||
| A3 =45 | 9 / 0 | 8 / 0 | 1 / 35 | 4 / 0 | 3 / 10 | ||
| A4 =15 | 9 / 0 | 3 / 10 | 6 / 0 | 10 / 0 | 7 / 5 |
Для примера обратимся к табл. 9. В ней построен цикл пересчета для свободной клетки (1, 1). Оценка этой клетки по формуле (6) равна
d ij = c11 – c15 + c35 – c34 + c24 – c21 = 5 – 1 + 3 – 4 + 6 – 3 = 6.
Это означает, что при сдвиге по построенному циклу единицы груза стоимость перевозок по сравнению со стоимостью плана перевозок табл. 9 возрастет на 6 единиц.
Вернемся к общему случаю. Имеются три возможности для оценки свободной клетки.
1. Если d ij > 0, то Dz > 0, т.е. сдвиг в рассматриваемую свободную клетку (i, j) приводит к удорожанию перевозок, что удаляет от оптимального решения.
2. Если d ij = 0, то Dz = 0, т.е. сдвиг по циклу пересчета не влияет на стоимость перевозок.
3. Если d ij < 0, то Dz < 0, т.е. сдвиг в рассматриваемую свободную клетку (i, j) уменьшает стоимость перевозок. В этом случае следует определить максимальное значение x0, на которое можно произвести сдвиг по циклу пересчета. Оно находится из соображений неотрицательности решений и равно минимальному из значений x–ij – так символически можно обозначить значения базисных неизвестных в отрицательных клетках, т.е.
x0 =min { x–ij } (7)
Осуществим сдвиг по циклу пересчета данной свободной клетки на это число до (7). Базисную клетку, в которой достигается минимум (7), удалим из базиса и сделаем свободной. Ее место займет данная свободная клетка (i, j) со значением x0 неизвестного xij.
Таким образом, подучим новое базисное решение. Значение формы z при переходе к новому решению уменьшится на величину – Dz = d ij x0.
Из проведенных рассуждении следует важный вывод: базисное решение является оптимальным, если среди оценок свободных клеток нет отрицательных, причем, если все оценки свободных клеток положительны, то оптимальное решение единственно, если же некоторые оценки равны нулю, то оптимальное решение не единственно.
Алгоритм распределительного метода
1. Проверяют, является ли модель транспортной задачи закрытой. Если модель открытая, то, введя фиктивный пункт отправления (назначения) с нулевыми удельными стоимостями перевозок, сводят ее к закрытой модели.
2. Находят исходное допустимое базисное решение, например, методом наименьшей стоимости или по правилу северо-западного угла, заполняя базисные клетки соответствующими значениями базисных неизвестных.
3. Вычисляют оценки свободных клеток для полученного базисного решения. Если среди оценок нет отрицательных, то исследуемое базисное решение является оптимальным. Подсчитывают стоимость перевозок.
4. Если среди оценок свободных клеток найдется хотя бы одна отрицательная, то для одной из свободных клеток с отрицательной оценкой строят ее цикл пересчета. Осуществляют сдвиг по этому циклу на число x0, вычисленное по формуле (7). Получив новое базисное решение, переходят к пункту 3.
Замечание 1. Если имеется несколько свободных клеток с отрицательными оценками, то предпочтение среди них можно отдать клетке с минимальной удельной стоимостью. У этой рекомендации нет какого-либо серьезного обоснования, кроме интуитивного соображения о том, что в первую очередь следует заполнять клетки с минимальной удельной стоимостью.
Замечание 2. Иногда минимальное значение x0 достигается в нескольких базисных клетках. В этом случае удаляют ту из базисных клеток, в которой содержится наибольшая удельная стоимость cpq. В остальных базисных клетках, где достигается минимальное значение x0, неизвестные при сдвиге по циклу принимают значение 0, т.е. получается вырожденное базисное решение. Вырожденным называется базисное решение, в котором некоторые базисные неизвестные равны 0.
Замечание 3. В тех случаях, когда базисное решение вырождено, может оказаться, что минимальное значение x0 равно нулю. В такой ситуации нуль сдвигают в свободную клетку и она становится базисной, а базисная клетка, где стоял этот нуль ранее, становится свободной.
Наиболее затруднительным в приведенном алгоритме является вычисление оценок свободных клеток, поскольку требует построения цикла пересчета для каждой свободной клетки. Эта процедура облегчена в методе потенциалов.
Метод потенциалов
По методу потенциалов пунктам отправления А1, А2,..., Ат приписывают потенциалы a1, a2,..., a m, а пунктам назначения В1, В 2,..., Вn приписывают потенциалы b1, b2,..., b n. Значения потенциалов находят из системы линейных уравнений вида
a p + b q = c pq (8)
где c pq — удельная стоимость в базисной (!) клетке (р, q). Число базисных клеток равно т + п – 1, а число потенциалов равно т + п, поэтому, система линейно независимых уравнений вида (8) недоопределена и, следовательно, один из потенциалов можно задать произвольно.
Подставим выражения (8) удельных стоимостей через потенциалы в формулу (6), получим
d ij = cij – cik + clk – … + cst – csj =
= cij – a i – b k + a l + b k – … + a s + b t – a s – b j = cij – a i – b j .
Таким образом, оценка свободной клетки (i, j) равна
d ij = cij – (a i + b j ). (9)
Таблица 10.
| ai \ bj | b1=90 | b2=15 | b3=20 | b4=80 |
| a1 =55 | ||||
| a2 =75 | ||||
| a3 =50 | ||||
| a4 =25 |
Пример 2. Решить транспортную задачу, данные которой приведены в табл. (10). В первом ее столбце указаны запасы груза в четырех пунктах отправления, а в первой строке — потребности пунктов назначения. В левых верхних углах остальных клеток таблицы помещены удельные стоимости перевозок.
Таблица 11.
| ai \ bj | b1=90 | b2=15 | b3=20 | b4=80 |
| a1 =55 | 12 / 50 | 8 / 0 | 6 / 0 | 3 / 5 |
| a2 =75 | 9 / 0 | 4 / 0 | 5 / 0 | 3 / 75 |
| a3 =50 | 7 / 35 | 5 / 15 | 10 / 0 | 10 / 0 |
| a4 =25 | 6 / 5 | 8 / 0 | 5 / 20 | 9 / 0 |
Убедившись в том, что модель рассматриваемой задачи закрытая, распределим груз по методу наименьшей стоимости. Исходное базисное решение заносим в табл. 11. Стоимость полученного плана перевозок равна z =50*12+5*3+75*3+35*7+15*5+5*6+20*5=1290. :
Для оценки свободных клеток табл. 11 по методу потенциалов в соответствии с формулой (8) составим для базисных (!) клеток табл. 11 систему уравнений
a 1 + b 1 = 12, a 1 + b 4 = 3,
a 2 + b 4 = 3, (10)
a 3 + b 1 = 7, a 3 + b 2 = 5,
a 4 + b 1 = 6, a 4 + b 3 = 5,
из которой найдем потенциалы a i, b j, i, j = 1, 2, 3, 4. Для наглядности уравнения в системе (10) расположены также как базисные клетки в матрице перевозок, см. табл. 11.
Положим в системе (10) a 1 = 3, тогда из уравнений 1-й строки имеем b 1 = 9, b 4 = 0.
Далее, используя ранее вычисленные значения, из 2-й строки системы (10) получим a 2 = 3, из 3-й — a 3 = –2, b 2 = 7, из 4-й — a 4 = –3, b 3 = 8. Запишем эти потенциалы в табл. 12.
Таблица 12.
 ai \ bj ai \ bj
| b1=90 | b2=15 | B3=20 | b4=80 |
| a1 =55 | 12 / 50 | 8 / –2 | 6 / –5 | 3 / 5 |
| a2 =75 | 9 / –3 | 4 / –6 | 5 / –6 | 3 / 75 |
| a3 =50 | 7 / 35 | 5 / 15 | 10 / 4 | 10 / 12 |
| a4 =25 | 6 / 5 | 8 / 4 | 5 / 20 | 9 / 12 |
Заметим, что для вычисления потенциалов нет необходимости выписывать систему (10). Можно в табл. 12 задать один из потенциалов и, двигаясь в табл. 12 через базисные клетки, вычислить последовательно остальные потенциалы, используя равенство (8).
Вычислим по формуле (9) оценку каждой свободной клетки табл. 12 и занесем ее в знаменатель этой клетки:
d 12 = c12 – (a 1 + b 2 ) = 8 – (3 + 7) = –2,
d 13 = c13 – (a 1 + b 3 ) = 6 – (3 + 8) = –5,
d 21 = c21 – (a 2 + b 1 ) = 9 – (3 + 9) = –3,
d 22 = c22 – (a 2 + b 2 ) = 4 – (3 + 7) = –6,
d 23 = c23 – (a 2 + b 3 ) = 5 – (3 + 8) = –6,
d 33 = c33 – (a 3 + b 3 ) = 10 – (–2 + 8) = 4,
d 34 = c34 – (a 3 + b 4 ) = 10 – (–2 + 0) = 12,
d 42 = c42 – (a 4 + b 2 ) = 8 – (–3 + 7) = 4,
d 44 = c44 – (a 4 + b 4 ) = 9 – (–3 + 0) = 12.
Оценки свободных клеток, как и потенциалы, удобно вычислять непосредственно в таблицах, используя формулу (9).
Выберем в табл. 12 свободную клетку (2, 2) с отрицательной оценкой d 22 = -6 (см. выше замечание 1). Построим цикл пересчета этой клетки, означим его так, чтобы вершина цикла в клетке (2, 2) имела знак "+". Отрицательным вершинам цикла соответствуют значения базисных неизвестных x–11 = 50, x–24 = 75, x–32 = 15. Находим
x0 =min { x–11, x–24, x–32} = min {50, 75, 15} = x–32 = 15.
Так какминимум достигается в клетке (3, 2), то, осуществив сдвиг по циклу пересчета на 15, клетку (3, 2) удаляем из числа базисных (она становится свободной). Клетка (2, 2) становится базисной, при этом x22 = 15. Переходим к табл. 13. Снова вычисляем по формулам (8) потенциалы, задав какой-нибудь из них, например a 2 = 3.
 Таблица 13.
Таблица 13.
| ai \ bj | b1=90 | b2=15 | B3=20 | b4=80 |
| a1 =55 | 12 / 35 | 8 / –4 | 6 / –5 | 3 / 20 |
| a2 =75 | 9 / –3 | 4 / 15 | 5 / –6 | 3 / 60 |
| a3 =50 | 7 / 50 | 5 / 6 | 10 / 4 | 10 / 12 |
| a4 =25 | 6 / 5 | 8 / 4 | 5 / 20 | 9 / 12 |
Уместно заметить, что выбор того или иного значения для задаваемого потенциала сказывается на значениях всех потенциалов следующим образом. Если все вычисленные потенциалы, например, для пунктов отправления увеличить (уменьшить) на одно и тоже число, то все потенциалы для пунктов назначения уменьшатся (увеличатся) на то же число. Вычисляем теперь оценки свободных клеток табл. 13 по формулам (9). Выберем в табл. 13 свободную клетку (2, 3) с отрицательной оценкой d23 = –6. Построив для этой клетки цикл пересчета, осуществляем сдвиг по нему на
x0 = min { x–11, x–24, x–43} = min {35, 60, 20} = x–43 = 20.
Клетка (2, 3) становится базисной вместо клетки (4, 3), которая становится свободной. Переходим к табл. 14.
 Таблица 14.
Таблица 14.
| ai \ bj | b1=90 | b2=15 | B3=20 | B4=80 |
| a1 =55 | 12 / 15 | 8 / –4 | 6 / –1 | 3 / 40 |
| a2 =75 | 9 / –3 | 4 / 15 | 5 / 20 | 3 / 40 |
| a3 =50 | 7 / 50 | 5 / 6 | 10 / 10 | 10 / 12 |
| a4 =25 | 6 / 25 | 8 / 10 | 5 / 6 | 9 / 12 |
Вычислим потенциалы и оценки свободных клеток табл. 14. В ней одна свободная клетка (2, 1) имеет отрицательную оценку d21 = –3. По циклу пересчета этой клетки осуществляем сдвиг на
x0 = min { x–11, x–24 } = min {15, 40} = x–11 = 15.
Клетка (2,1) становится базисной вместо клетки (1,1), которая становится свободной. Переходим к табл. 15.
Таблица 15.
| ai \ bj | b1=90 | b2=15 | B3=20 | B4=80 |
| a1 =55 | 12 / 3 | 8 / 4 | 6 / 1 | 3 / 55 |
| a2 =75 | 9 / 15 | 4 / 15 | 5 / 20 | 3 / 25 |
| a3 =50 | 7 / 50 | 5 / 6 | 10 / 10 | 10 / 12 |
| a4 =25 | 6 / 25 | 8 / 10 | 5 / 6 | 9 / 12 |
Все оценки свободных клеток табл. 15 положительны, следовательно, табл. 15 содержит оптимальное решение, в котором
x14 = 55, x21 = 15, x22 = 15, x23 = 20, x24 = 25, x31 = 50, x41 = 25.
Остальные неизвестные равны нулю. Полученное решение указывает оптимальный план перевозок. Например, x23 = 50 означает, что из 2-го пункта отправления в 3-й пункт назначения следует перевезти 50 ед. груза. Общая стоимость перевозок по этому плану будет наименьшей по сравнению с любым другим планом. Она равна
z = 55 • 3 + 15 • 9 + 15 • 4 + 20 • 5 + 25 • 3 + 50 • 7 + 25 • б = 1035.
Полезно еще раз обсудить экономический смысл оценок свободных клеток. Как отмечалось ранее, оценка свободной клетки для данного базисного решения равна изменению стоимости перевозок при сдвиге по циклу пересчета рассматриваемой свободной клетки на единицу груза. Оценка свободной клетки (2, 1) табл. 14 равна d21 = –3. Следовательно, при переходе от табл. 14 к табл. 15, когда был осуществлен сдвиг на 15 ед. груза по циклу пересчета клетки (2, 1), стоимость перевозок уменьшилась на (–Dz) = 3 • 15 = 45, т.е. план перевозок, соответствующий базисному решению, содержащемуся в табл. 14, дороже оптимального плана на 45 единиц стоимости и стоит 1080 единиц.
Замеча