БИЛЕТЫПО ФИЗИКЕ
1. Меха́ника — область физики, изучающая движение материальных тел и взаимодействие между ними. Движением в механике называют изменение во времени взаимного положения тел или их частей в пространстве[1]. Важнейшими разделами механики являются классическая механика, релятивистская механика и квантовая механика
Пространственная система отсчета СО =
тело отсчета + пространственная система координат. Вид одномерной ПСО приведен на рис. 1.2. Положение тела отсчета совпадает с точкой O на оси OX.Теперь в каждой точке пространства расположим часы, которые предварительно были синхронизованы. Пространственную систему отсчета и эту систему часов назовем пространственно-временной системой отсчетаПВСО или сокращенно - системой отсчета (СО). ПСО + система часов = ПВСО.
Кинема́тика (греч. κινειν — двигаться) в физике — раздел механики, изучающий математическое описание (средствами геометрии, алгебры,математического анализа…) движения идеализированных тел (материальная точка, абсолютно твердое тело, идеальная жидкость), без рассмотрения причин движения (массы, сил и т. д.). Исходные понятия кинематики — пространство и время. Например, если тело движется по окружности, то кинематика предсказывает необходимость существования центростремительного ускорения без уточнения того, какую природу имеет сила, его порождающая. Причинами возникновения механического движения занимается другой раздел механики — динамика.Различают классическую кинематику, в которой пространственные (длины отрезков) и временные (промежутки времени) характеристики движения считаются абсолютными, то есть не зависящими от выбора системы отсчёта, и релятивистскую. В последней длины отрезков и промежутки времени между двумя событиями могут изменяться при переходе от одной системы отсчёта к другой. Относительной становится также одновременность. В релятивистской механике вместо отдельных понятий пространство и время вводится понятие пространства-времени, в котором инвариантным относительно преобразований Лоренца является величина, называемая интервалом.
Дина́мика (греч. δύναμις — сила) — раздел механики, в котором изучаются причины возникновения механического движения. Динамика оперирует такими понятиями, как масса, сила, импульс, энергия.
Материа́льная то́чка (частица) — простейшая физическая модель в механике — идеальное тело, размеры которого равны нулю, можно также считать размеры тела бесконечно малыми по сравнению с другими размерами или расстояниями в пределах допущений исследуемой задачи. Положение материальной точки в пространстве определяется как положение геометрической точки.Практически под материальной точкой понимают обладающее массой тело, размерами и формой которого можно пренебречь при решении данной задачи.[1]
2. Кинема́тика точки — раздел кинематики, изучающий математическое описание движения материальных точек. Основной задачей кинематики является описание движения при помощи математического аппарата без выяснения причин, вызывающих это движение.Движение любого объекта в кинематике изучают по отношению к некоторой системе отсчета, включающей:
Тело отсчета;
Систему измерения положения тела в пространстве (систему координат);
Прибор для измерения времени (Часы).
Положение точки определяется набором обобщенных координат — упорядоченным набором числовых величин, полностью описывающих положение тела. В самом простом случае это координаты точки (радиус-вектора) в выбранной системе координат. Наиболее наглядное представление о радиус-векторе можно получить в евклидовой системе координат, поскольку базис в ней является фиксированным и общим для любого положения тела
.Радиус-вектор — Вектор, определяющий положение М. Т. в пространстве: 
. Здесь 
— координатырадиус-вектора. Геометрически изображается вектором, проведенным из начала координат к материальной точке. Зависимость радиус-вектора (или его координат 
) от времени 
называется законом движения.
Траектория — Годограф радиус-вектора, то есть — воображаемая линия, описываемая концом радиус-вектора в процессе движения. Иными словами, траектория — это линия вдоль которой движется М. Т. При этом закон движения выступает как уравнение, задающее траекторию параметрически. Длину участка траектории между начальным и конечным моментами времени часто называют пройденным расстоянием, длиной пути или вульгарно — путем и обозначают буквой S. При таком описании движения S выступает в качестве обобщенной координаты, а законы движения в этом случае записывается в виде S = S(t) и аналогичны соответствующим законам для координат. Например закон равноускоренного криволинейного движения может быть записан в виде:
,
Радиус-вектора и вектор перемещения (черные стрелки). Вектора средней и мгновенных скоростей (Зеленые стрелки). Траектория (красная линия)
Где: 
— модуль начальной скорости, а 
— Тангенциальное ускорение.
Описание движения при помощи понятия траектории — один из ключевых моментов классической механики. В квантовой механике движения носит бестраекторный характер, а само понятие траектории теряет смысл.
Перемещение — векторная физическая величина, равная разности радиус-векторов в конечный и начальный моменты времени:
.
Иными словами, перемещение — это приращение радиус-вектора за выбранный промежуток времени.
Средняя скорость — векторная физическая величина равная отношению вектора перемещения к промежутку времени, за который происходит это перемещение:
.
Мгновенная скорость — векторная физическая величина, равная первой производнойот радиус-вектора по времени:
.
Характеризует быстроту перемещения материальной точки. Мгновенную скорость можно определить как предел средней скорости при устремлении к нулю промежутка времени, на котором она вычисляется:
.
Единица измерения скорости в системе СИ— м/с, в системе СГС — см/с. Мгновенная скорость всегда направлена по касательной к траектории.
Мгновенное ускорение — векторная физическая величина, равная второй производной от радиус-вектора по времени и, соответственно, первой производной от мгновенной скорости по времени:
.
Разложение ускорения по сопутствующему базису
Характеризует быстроту изменения скорости. Единица ускорения в системе СИ— м/с², в системе СГС — см/с². В случае движения в плоскости вектор ускорения можно разложить по сопутствующему базису: на вектор нормального и тангенциального ускорения:
.
Здесь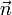 
— единичный вектор нормали, 
— единичный вектор касательной. Величина 
называется нормальным ускорением и характеризует скорость изменения направления движения. Нормальное ускорение выражается через мгновенную скорость и радиус кривизны траектории:
.
В случае движения по окружности нормальное ускорение называется центростремительным. Как видно из предыдущей формулы, при движении по окружности с постоянной скоростью нормальное ускорение постоянно по модулю и направлено к центру окружности.
Величина 
называется тангенциальным ускорением и характеризует величину изменения модуля скорости:
.
Закон равноускоренного движения
Равноускоренное движение в поле тяжести Земли
Закон равноускоренного движения получается в результате решения простейшего дифференциального уравнения вида:
Общее решение этого уравнения дается формулой:
;
Здесь 
и 
— произвольные константы, соответствующие начальной координате и начальной скорости.
Движение с постоянным ускорением 
называют равноускоренным. Движение с постоянным ускорением подчиняется закону:
;
.
При этом уравнения движения в координатной форме имеют аналогичный вид:
;
.
В этом случае часто говорят о равноускоренном движении, если знаки 
и 
совпадают и о равнозамедленном, если и 
имеют противоположные знаки. При этом знак каждой из величин зависит от начального выбора системы отсчета.
Частный случай равноускоренного движения — равномерное движение. В этом случае 
. Тогда движение описывается закону:
В робототехнике, есть две основные задачи кинематики:
прямая и обратная.
Рассмотрим эти задачи на стандартном примере манипулятора.
Прямая задача — это вычисление положения (X, Y, Z) рабочего органа манипулятора по его кинематической схеме и заданной ориентации (A1, A2… An) его звеньев (n — число степеней свободы манипулятора, A — углы поворота).
Обратная задача — это вычисление углов (A1, A2… An) по заданному положению (X, Y, Z) рабочего органа и опять же известной схеме его кинематики.
Т.о., решение прямой задачи говорит — где будет находиться рабочий орган манипулятора, при заданных углах его суставов, а обратная задача, наоборот, говорит: как нужно «вывернуться» манипулятору, чтобы его рабочий орган оказался в заданном положении.
Очевидно, что более распространённой и важной является именно обратная задача кинематики.
Но нужно иметь в виду, что эта задача редко может быть решена однозначно.
Дело в том, что хотя для углов (A1, A2,..., An) всегда существует ЕДИНСТВЕННОЕ положение (X, Y, Z) рабочего органа, но не факт, что для положения (X, Y, Z) отыщется такая же единственная комбинация углов (A1, A2,..., An).
Скорее всего, достичь заданного положения (X, Y, Z) возможно и при другой комбинации углов (A1', A2',..., An').
При решении обратной задачи аналитически, эта неоднозначность проявляется в явном виде (например, через квадратные корни)
3.
| При криволинейном движении скорость направлена по касательной к траектории. Поскольку направление скорости постоянно изменяется, то криволинейное движение - всегда движение с ускорением, в том числе, когда модуль скорости остается неизменным | 
|
В общем случае ускорение направлено под углом к скорости. Составляющая ускорения, направленная вдоль скорости, называется тангенциальным ускорением  . Она характеризует изменение скорости по модулю.
| |
| |
Составляющая ускорения, направленная к центру кривизны траектории, т.е. перпендикулярно (нормально) скорости, называется нормальным ускорением . Она характеризует изменение скорости по направлению.
| |
| |
| Здесь R - радиус кривизны траектории в данной точке.Тангенциальное и нормальное ускорение взаимноперпендикулярны, поэтому модуль полного ускорения | |
|
4. В случае равномерного вращения тела формой траектории его материальных точек являются окружности радиусов R i, где i - порядковый номер выбранной точки тела. При этом модули их скоростей остаются постоянными V i = const.
Положение материальной точки в пространстве определяется углом ее поворота f относительно начального значения и радиусом вектором R i. За один оборот радиус-вектор поворачивается на угол2p, а его конец проходит путь равный 2p·Ri.
Для описания характера вращения используются следующие характеристики: V - линейная скорость и w - угловая скорость. Определение угловой скорости вводится по аналогии с линейной.
Мгновенная угловая скорость равна скорости изменения угла во времени w = df/dt.
Единицей измерения величины w является радиан в секунду (рад/c). Направление вектора угловой скорости задается по правилу правого винта
При равномерном вращении
V = 2pR/T,
w = f/Dt = 2p/T,
где T - время одного полного оборота по окружности (период вращения).
Линейная скорость направлена по касательной в каждой точке траектории.
Угловая и линейная скорости связаны соотношением V = w·R.
Для описания вращательного движения вводится понятие частоты вращения n, которая равна числу оборотов тела в единицу времени
n = N/Dt,
где N - число оборотов материальной точки за время Dt.
Период обращения связан с частотой вращения соотношением T = 1/n.
Криволинейная траектория Частным случаем такого движения является движение тела по окружности неизменного радиуса с постоянным ускорением. Ускорение вращательного движения тела (угловое ускорение) равно
e = d w /dt
Если ускорение с течением времени не изменяется, то
e = D w /Dt,
где D w = w - w 0 - разность угловых скоростей в произвольный момент времени t и в момент времени t = 0.
Угловое ускорение также как и скорость является векторной величиной. Оно направлено вдоль оси вращения (параллельно вектору угловой скорости, в случае ее возрастания со временем и антипараллельно - в случае ее убывания).
Поскольку ускорение является векторной величиной, то его можно разложить на составляющие. При описании вращательного движения принято использовать понятия касательного и нормального направлений. Соответственно вводятся понятия тангенциального (касательного) и центростремительного (нормального) ускорений.
| Тангенциальное ускорение at характеризует изменение вектора линейной скорости по величине at = dV/dt и направлено по касательной в данной точке траектории. Нормальное ускорение an характеризует изменение вектора линейной скорости по направлению an = V2/R = w2·R и сориентировано вдоль нормали (см. рис. 3, на котором показана траектория движения тела, причем движение происходит с нарастающей скоростью). a = an·n + at·t, где n и t - единичные векторы вдоль нормального и тангенциального направлений. Модуль вектора ускорения равен a = (an2 + at2)1/2. Тангенциальное и угловое ускорения связаны между собой соотношением at = e·R. |
5. Законы динамики Ньютона
законы или аксиомы движения (в формулировке самого Ньютона по книге «Математические начала натуральной философии» 1687 года): «I. Всякое тело продолжает удерживаться в своем состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменять это состояние. II. Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует. III. Действию всегда есть равное и противоположное противодействие, иначе взаимодействия двух тел друг на друга между собой равны и направлены в противопо-ложные стороны».
И́мпульс (Количество движения) — векторная физическая величина, являющаяся мерой механического движениятела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:
.
Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) замкнутой системы есть величина постоянная.
В классической механике закон сохранения импульса обычно выводится как следствие законов Ньютона. Из законов Ньютона можно показать, что при движении в пустом пространстве импульс сохраняется во времени, а при наличии взаимодействия скорость его изменения определяется суммой приложенных сил.
Как и любой из фундаментальных законов сохранения, закон сохранения импульса описывает одну изфундаментальных симметрий, — однородность пространства.
6 Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массывращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно — если в задаче есть центральная или осевая симметрия, но не только в этих случаях).
Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси —псевдоскаляр.
Момент импульса замкнутой системы сохраняется.
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, (проведенного от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют всопротивлении материалов).
Момент силы — производная по времени от момента импульса,
,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
,
То есть, если I постоянная, то
,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Между моментом силы и импульсом силы легко прослеживается аналогия. Сравните:
и 
,
где аналогом силы является момент силы, а аналогом импульса - момент импульса.
Происхождение названия < момент импульса > станет ясным, если мы рассмотрим в качестве равномерно движущегося тела по окружности материальную точку. Момент инерции тела в этом случае равен произведению массы тела m на квадрат расстояния R от тела до оси вращения: 
7. Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта, в которой справедлив первый закон Ньютона (закон инерции): все свободные тела (то есть такие, на которые не действуют внешние силы или действие этих сил компенсируется) движутся прямолинейно и равномерно или покоятся[1]. Эквивалентной является следующая формулировка, удобная для использования в теоретической механике
Если скорости относительного движения ИСО, реализуемых действительными телами, могут принимать любые значения, связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Галилея.
В специальной теории относительности скорости относительного движения ИСО, реализуемых действительными телами, не могут превышать некоторой конечной скорости «C » (скорость распространения света в вакууме) и связь между координатами и моментами времени любого «события» в разных ИСО осуществляется преобразованиями Лоренца
Преобразова́ния Галиле́я — в классической механике (механике Ньютона) преобразования координат и скорости при переходе от однойинерциальной системы отсчета (ИСО) к другой[1]. Термин был предложен Филиппом Франком в 1909 году.[2] Преобразования Галилея подразумевают одинаковость времени во всех системах отсчета («абсолютное время»[3]) и выполнение принципа относительности (принцип относительности Галилея (см. ниже)).Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для скоростей, малых по сравнению со скоростью света в пустоте и в ограниченном объёме пространства. Для скоростей вплоть до порядка скоростей движения планет в Солнечной системе (и даже бо́льших), преобразования Галилея приближенно верны с очень большой точностью.
Если ИСО S движется относительно ИСО S' с постоянной скоростью 
вдоль оси 
, а начала координат совпадают в начальный момент времени в обеих системах, то преобразования Галилея имеют вид:
или, используя векторные обозначения,
(последняя формула остается верной для любого направления осей координат).
Как видим, это просто формулы для сдвига начала координат, линейно зависящего от времени (подразумеваемого одинаковым для всех систем отсчета).
Из этих преобразований следуют соотношения между скоростями движения точки и её ускорениями в обеих системах отсчета:
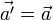
Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для малых скоростей 
(много меньше скорости света).
[править]Формула преобразования скоростей
Достаточно продифференцировать 
в формуле преобразований Галилея, приведенной выше, и сразу же получится приведенная в том же параграфе рядом формула преобразования скорости.
Приведем более элементарный, но и более общий вывод — для случая произвольного движения начала отсчета одной системы относительно другой (при отсутствии вращения). Для такого более общего случая, можно получить формулу преобразования скоростей, например, так.
Рассмотрим преобразование произвольного сдвига начала отсчета на вектор 
,
где радиус-вектор какого-то тела A в системе отсчета K обозначим за , а в системе отсчета K' — за 
,
подразумевая, как всегда в классической механике, что время 
в обеих системах отсчета одно и то же, а все радиус-векторы зависят от этого времени: 
.
Тогда в любой момент времени
и в частности, учитывая
,
имеем:
где:
— средняя скорость тела A относительно системы K;
— средняя скорость тела А относительно системы K';
— средняя скорость системы K' относительно системы K.
Если 
то средние скорости совпадают с мгновенными:
или короче
— как для средних, так и для мгновенных скоростей (формула сложения скоростей). 
Таким образом, скорость тела относительно неподвижной системы координат равна векторной сумме скорости тела относительно движущейся системы координат и скорости системы отсчета относительно неподвижной системы отсчета. Аналогично можно получить формулу преобразования ускорений при переходе из одной системы координат в другую, верную при условии, что эти системы движутся поступательно друг относительно друга: 
Инвариантность законов классической механики при переходе в движущуюся ИСО подразумевает в том числе и то, что ускорения, вызванные взаимодействием любых двух материальных точек должны быть направлены по прямой, соединяющей точки, противоположно друг другу. Этому требованию удовлетворяют преобразования Галилея.
Если в неподвижной ИСО ускорения, вызванные взаимодействием двух материальных точек, направлены по прямой, соединяющей точки, противоположно друг другу, то при переходе в движущуюся ИСО по Лоренцу, эти ускорения преобразуются так, что уже не будут направлены по прямой соединяющей точки.
Преобразования Лоренца не оставляют инвариантным направление ускорений, вызванных взаимодействием любых двух материальных точек. Классический закон преобразования такой 
.
8 Системой материальных точек называется такая их совокупность, в которой положение и движение каждой точки зависит от положения и движения всех точек данной системы.Часто систему материальных точек называют механической системой.Действующие на точки механической системы активные силы и реакции связей можно разделить на внешние и внутренние силы. Внутренними силами называют силы взаимодействия между материальными точками одной механической системы. Внешние силы - это силы взаимодействия точек данной механической системы с точками какой-либо другой системы.
Закон сохранения импульса системы точек выводится из второго закона Ньютона. Сначала записываем формулу второго закона для каждой точки системы, а затем полученные равенства складываем так, что слева получается производная по времени от вектора импульса системы точек, а справа - сумма всех действующих сил. Но по третьему закону Ньютона сумма сил, действующих между каждой парой точек, равна нулю, поэтому справа остается только сумма внешних сил.
закон сохранения импульса системы материальных точек: общий момент импульса системы относительно какой-либо неподвижной оси остается постоянным, если момент внешних сил относительно этой оси равен нулю
9. ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС МЕХ. СИСТЕМЫ
Доказательство
Повторим все вышеприведенные предложения; запишем n векторных равенств
(основное уравнение динамики для каждой м.т.) и сложим их.
И используются эти уравнения абсолютно точно так же - то есть для решения первой и второй задач динамики. Подробнее о задачах будет сказано дальше. Здесь же отметим, что записанные уравнения называются также диф. уравнениями поступательного движения твердого тела.
Поступательно движущееся тело в механике рассматривается как материальная точка.
Дифференциальные. уравнения поступательно движущегося тела и м.т., естественно, одинаковы.
При сложном движении твердых тел (в кинематике сложное движение тела рассматривается как результат сложения поступательного движения и вращательного или сферического) вышеприведенные уравнения описывают поступательную часть движения тела.
9. Движение тела переменной массы
В некоторых случаях тел связано с изменением их массы, например масса ракеты уменьшается вследствие истечения газов, образующихся при сгорании топлива, и т. п.
Произведем вывод уравнения движения тела переменной массы на примере движения ракеты. Если в момент времени t масса ракеты m, а ее скорость v, то по истечении времени dt ее масса уменьшится на dm и станет равной т-dm, а скорость станет равной v+dv. Изменение импульса системы за промежуток времени dt
где u - скорость истечения газов относительно ракеты. Тогда
здесь учтено, что dmdv - малое высшего порядка малости по сравнению с остальными слагаемыми. Если на систему действуют внешние силы, то dp=Fdt, поэтому
или
(1)
Второе слагаемое в правой части (1) называют реактивной силой Fp. Если u противоположен v по направлению, то ракета ускоряется, а если совпадает с v, то тормозится.
Таким образом, мы получили уравнение движения тела переменной массы
(2)
которое впервые было выведено И. В. Мещерским (1859-1935).
Рассмотрим случай отсутвтия воздействия внешних сил на ракету. Положим в уравнении (1) F=0 и будем считать, что скорость выбрасываемых газов относительно ракеты постоянна (ракета движется прямолинейно), получим
откуда
Значение постоянной интегрирования С определим из начальных условий. Если в начальный момент времени стартовая масса m0, а ее скорость ракеты равна нулю, то С = uln(m0). Следовательно,
Это соотношение называется формулой Циолковского.
Выражения (2) и (3) верны для нерелятивистских движений, т. е. для случаев, когда скорости v и u малы по сравнению со скоростью света в вакууме.
10. Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силыили сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы