Дан граф:
Присвойте вершинам графа 
попарно различные номера из диапазона 1, 2, …, n, где n – число вершин графа .
Представленные выше графы являются ориентированными, но наряду с каждым таким графом рассмотрите неориентированный граф, полученный из него заменой каждой дуги ребром. Последний граф далее обозначается как н- .
Номер i варианта контрольной работы, выполняемого студентом, определяет граф , который является предметом исследования в сформулированных ниже задачах.
1. Для графа и н- постройте матрицу смежности и матрицу инциденций. Для каждой вершины графа укажите полустепень исхода и захода. Для графа н- укажите степень каждой вершины.
2. Для графа н- определить, является ли он: а) связным; б) сильно связным. Найти все его компоненты сильной связности.
3. Найдите хроматическое число графа н- .
4. Ответьте на следующие вопросы и обоснуйте эти ответы:
а) является ли граф н- эйлеровым; если да, то найдите и укажите эйлеров цикл этого графа.
б) определите, является ли граф н- гамильтоновым; если да, то укажите гамильтонов цикл.
Решение
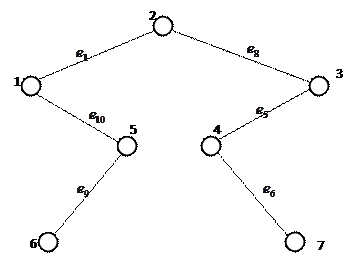
Пронумеруем произвольным образом вершины и ребра. Получим граф:
 |
Рис.1. Ориентированный граф
 |
|
|
 |
Рис.2. Неориентированный граф н- .
1. Представление графа с помощью квадратной булевой матрицы, отражающей смежность вершин, называется матрицей смежности, где
Для нашего ориентированного графа имеем матрицу смежности:
.
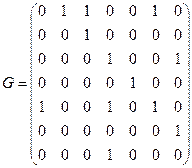Для неориентированного графа н- .матрица смежности имеет вид:
Представление графа с помощью матрицы, отражающей инцидентность вершин и ребер, называется матрицей инциденций, где для ориентированного графа
.
Для нашего ориентированного графа имеем матрицу инциденций:
.
Для неориентированного графа матрица инциденций имеет вид:
Для нашего неориентированного графа н- . имеем матрицу инциденций:
Количество ребер, инцидентных вершине v, называется степенью вершины v и обозначается d (v).
Найдем степени вершин графа н- :
d (1)=4, d (2)=2, d (3)=4, d (4)=4, d (5)=4, d (6)=3, d (7)=3.
Сделаем проверку правильности вычислений. Сумма степеней вершин графа должна быть равна удвоенному количеству ребер: 4+2+4+4+4+3+3=24-сумма степеней вершин графа, 12*2=24-удвоенное количество ребер. Вычисление выполнено верно.
Для графа число дуг, исходящих из узла v,, называется полустепенью исхода, а число входящих - полустепенью захода. Обозначим эти числа соответственно, 
и 
. Для исследуемого графа определим полустепень исхода и полустепень захода:
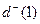=3 и 
=1; 
=1 и 
=1; 
=2 и 
=2; 
=1 и 
=3; 
=3 и 
=1; 
=1 и 
=2; 
=1 и 
=2.
Сделаем проверку правильности вычислений. Сумма полустепеней узлов орграфа равна удвоенному количеству дуг: 3+1+1+1+2+2+1+3+3+1+1+2+1+2=24- сумма полустепеней узлов орграфа, 12*2=24-удвоенное количество дуг. Вычисление выполнено верно.
Говорят, что две вершины в графе связаны, если существует соединяющая их цепь. Граф, в котором все вершины связаны, называется связным. Граф связен тогда и только тогда, когда его нельзя представить в виде объединения двух графов. Пусть 
- число вершин, 
-число ребер. Если
, (1)
то граф связен. У исследуемого графа н- число вершин =7, а число ребер =12. Подставим и в неравенство (1), тогда имеем:
, что равно 
- верно.
Из сказанного выше можно сделать вывод, что граф н- является связным.
Пусть G (V,E) – орграф (ориентируемый граф), v 
и v 
- его узлы. Говорят, что два узла сильно связаны, если существует путь как из v в v , так и из v в v . Если две любые пары вершин в орграфе сильно связаны, то орграф называется сильно связным.
Исследуем граф в нашей задаче (ориентированный), построив пути, связывающие каждую пару вершин этого графа:
1, 
,2; 2, 
, 3, 
,7, 
, 4, 
, 5, 
, 1
1, ,2, , 3; 3, ,7, , 4, , 5, , 1
1, ,2, , 3, 
, 4; 4, , 5, , 1
1, ,2, , 3, , 4, 
5; 5, , 1
1, ,2, , 3, , 4, 5, 
, 6 6, 
, 7, ,4, , 5, , 1
1, ,2, , 3, ,7 7, ,4, , 5, , 1
2, , 3 3, ,7, , 4, , 5, , 1, ,2
2, , 3, ,7, , 4, , 5, , 1 1, ,2;
2, , 3, , 4 4, , 5, , 1, ,2
2, , 3, , 4, 5; 5, , 1, ,2
2, , 3, , 4, 5, , 6 6, , 7, ,4, , 5, , 1, ,2
2, , 3, ,7 7, , 4, , 5, , 1, ,2
3, ,7, , 4, , 5, , 1 1, ,2, , 3;
3, ,7, , 4, , 5, , 1, ,2 2, , 3;
3, , 4 4, , 5, , 1, ,2, , 3;
3, ,7, , 4, , 5 5, , 1, ,2, , 3;
3, , 4, 5, , 6 6, , 7, ,4, , 5, , 1, ,2, , 3;
3, ,7 7, , 4, , 5, , 1, ,2, , 3;
4, , 5, , 1 1, ,2, , 3, , 4
4, , 5, , 1, ,2 2, , 3, , 4
4, , 5, , 1, ,2, , 3; 3, , 4
4, , 5 5, , 1, ,2, , 3, , 4;
4, 5, , 6 6, , 7, ,4
4, 5, , 6, , 7 7, , 4
5, , 1 1, ,2, , 3, , 4, 5
5, , 6 6, , 7, ,4, , 5
5, , 6, , 7 7, ,4, , 5
6, , 7 7, ,4, , 5, , 6
В исследуемом графе связаны все пары узлов, поэтому граф н- является сильно связным.
Число компонентов связности графа G обозначается 
(G). Граф G является связным тогда и только тогда, когда (G)=1, если (G)>1, то граф несвязный.
Компонента сильной связности графа - это максимальный сильно связный его подграф. В нашем случае это: 6, , 7, ,4, , 5, , 1, ,2, , 3.
Исследуемый граф н- не эйлеров, так как у него есть вершины с нечетной степенью (таковыми являются, например, вершины 6 и7). Степень вершины - число ребер, инцидентных этой вершине.
В силу того, что граф н- не эйлеров, он не содержит эйлерова (проходящего через все ребра по одному разу) цикла.
Эйлеров цикл должен содержать каждое ребро графа ровно один раз. Нами цикл рассматривается как множество ребер. Простым циклом называется замкнутая простая цепь (все вершины цепи различны и начало цепи совпадает с ее концом).
Если граф имеет простой цикл, содержащий все вершины графа по одному разу, то такой цикл называется гамильтоновым циклом, а граф называется гамильтоновым графом. Заметим, что гамильтонов цикл не обязательно содержит все ребра графа. Очевидно, что гамильтоновым может быть только связный граф.
Пусть 
есть минимальная степень вершин графа, - число вершин, тогда, если 
, то граф G является гамильтоновым (теорема Дирака). Это условие достаточное, но оно не является необходимым.
Для нашего графа н- имеем: =2, =7, 
- это неравенство неверно. Необходимое условие не выполняется, тогда для исследуемого графа н- требуется дополнительное исследование.
Раскраской графа называется такое приписывание цветов его вершинам, что любые две смежные его вершины имеют разный цвет. Наименьшее возможное число цветов в раскраске графа G называется его хроматическим числом и обозначается как 
.
.
Алгоритм раскрашивания заключается в следующем:
1) Строится матрица М = { 
} максимальных независимых множеств вершин графа.
2) На основе матрицы М строится минимальное покрытие П={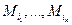 
}, где 
, множества вершин графа.
3) Производится раскраска графа G путем присвоения вершинам подмножества 
покрытия П одного и того же цвета, отличного от цвета вершин других подмножеств из покрытия П.
Понятно, что хроматическое число графа G есть число k, равное числу подмножеств минимального покрытия П.
Проиллюстрируем работу алгоритма на примере рассматриваемого нами графа.
Вначале напомним некоторые понятия и определения из теории графов.
Подмножество вершин 
графа G называется независимым, если никакие две вершины не соединены ребром. Подмножество , содержащее максимальное число независимых вершин графа G, называется максимальным независимым множеством.
Построим матрицу М для рассматриваемого примера н- графа. Доказано, что задача построения максимального независимого множества вершин графа является NP-полной, т.е. ее решение в общем случае можно получить только перебором всех вариантов. Однако существуют классы графов (например, графы – деревья), для которых можно построить упомянутые множества без перебора.
Для нашего примера искомая матрица может иметь следующий вид:
.
Условимся считать, что строки матрицы пронумерованы числами 1,2,…,7 сверху вниз и каждая строка соответствует вершине графа с соответствующим номером. Столбцам графа поставим в соответствие символы 
(слева направо), где каждый столбец соответствует некоторому максимальному независимому подмножеству вершин рассматриваемого графа. Так, например, символу (столбцу)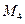 
соответствует максимальное независимое подмножество вершин {2,5,7} (1 ставится в той строке, номер которой соответствует номеру принадлежащей 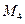вершине, и 0 - в противном случае). Обозначим через 
={ 
} множество всех максимально независимых подмножеств вершин графа G. Далее из множества выбираем минимальное количество таких подножеств, которые образуют покрытие П = { 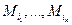} множества Х вершин графа G.
Напомним, что покрытием П = { 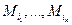} множества вершин Х графа называется такая совокупность подмножеств, которая удовлетворяет двум следующим условиям:
1). 
, где Х- множество вершин графа G.
2). 
.
Минимальным покрытием множества Х вершин графа называется такое, которое содержит минимальное число подмножеств множества П.
Заметим, что в приведенной выше матрице М перечислены (ради сокращения размерности приводимой матрицы) не все максимальные независимые подмножества вершин графа, однако и этот неполный набор максимальных независимых подмножеств уже даст минимально возможную раскраску, т.е. позволят найти хроматическое число графа.
В нашем примере можно указать по крайней мере два различных минимальных покрытия:
П1={ 
}= {{2,4,6},{1,7},{3,5}} и П2=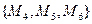 
={{2,5,7},{1,4},{3,6}}.
На основе этих данных получаем две различные раскраски графа, содержащие по три краски.
1) Покрытию П1 соответствует, например, раскраска {2,4,6}- белые,{1,7}- красные,{3,5}- черные.
2). Покрытию П2 соответствует, например, раскраска {2,5,7} - красные,{1,4} - черне,{3,6} - белые.
Докажем теперь, что полученные раскраски минимальны по числу использованных цветов, т.е. хроматическое число 
(G) графа в нашем примере равно 3.
В нашем исходном графе имеется подграф, изображенный на рис.3, который, как легко видеть, требует для раскраски ровно три цвета. Следовательно, исходный граф также не может быть раскрашен меньшим числом красок. Однако такие раскраски (два варианта) мы указали в явном виде, следовательно, хроматическое число (G) графа действительно равно 3.
1 
3
Рис.3.
В заключение отметим, что в общем случае задача раскраски вершин графа имеет не единственное решение.
Ниже на рис.4 приведен один из вариантов раскраски рассматриваемого графа.
 |
Рис.4
Деревом называется связный граф без циклов. Остовым подграфом графа называется подграф, содержащий все вершины. Остовый подграф, являющийся деревом, называется остовом или каркасом. Несвязный граф не имеет остова. Связный граф может иметь много остовов.
Рассмотрим следующий алгоритм построения остова:
1) Возьмем произвольный цикл графа и вынем из него ребро (взяли цикл с вершинами 1,2,3 и вынули ребро ) так, чтобы граф оставался связным, т.е. две любых вершины графа были соединены цепью.
 |
2) 
Возьмем другой произвольный цикл графа и вынем из него ребро (взяли цикл с вершинами 1,5,6 и вынули ребро 
) так, чтобы граф оставался связным, т.е. две любых вершины графа были соединены цепью.
3) 
Возьмем другой произвольный цикл графа и вынем из него ребро (взяли цикл с вершинами 3,4,7 и вынули ребро 
) так, чтобы граф оставался связным, т.е. две любых вершины графа были соединены цепью.
4) Возьмем другой произвольный цикл графа и вынем из него ребро (взяли цикл с вершинами 1,2, 3,4,5 и вынули ребро 
) так, чтобы граф оставался связным, т.е. две любых вершины графа были соединены цепью.
5) Возьмем другой произвольный цикл графа и вынем из него ребро (взяли цикл с вершинами 1,2, 3,4,7, 6, 5 и вынули ребро 
) так, чтобы граф оставался связным, т.е. две любых вершины графа были соединены цепью.
 |
Полученный подграф не содержит циклов и связен, поэтому является остовом.