Определение. Геометрическое место середин хорд поверхности второго порядка одного и того же неасимптотического направления { l; m; n } называется диаметральной плоскостью поверхности второго порядка, сопряженной направлению { l; m; n }.
Пусть М 1 М 2 – хорда с серединой в точке M 0 => 
=> Q =0=> 
(*)
- текущая точка => 
(*) превратиться в
(11) – уравнение геометрического места середин хорд.
Рассмотрим уравнение (11) (уравнение первой степени), выделим в нем коэффициенты при x, y и z:
(11.1)
Пусть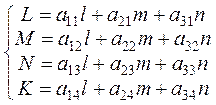 
(12)
(11.1)
Докажем, что это уравнение первой степени методом от противного. Предположим не первой => нулевой.
(13) 
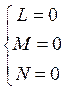, но 
- асимптотическое направление, что противоречит условию. Следовательно, уравнение (11) – это уравнение первой степени.
Определение. Направление вектора 
, координаты которого удовлетворяют условию (13), называется особым направлением поверхности (2).
Особое направление не имеет сопряженной диаметральной плоскости и является асимптотическим. Но не каждое асимптотическое направление является особым.
Взаимно сопряженные направления поверхности.
Определение. Вектор 
называется сопряженным к вектору , если первый вектор параллелен диаметральной плоскости сопряженной направлению вектора 
.
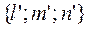|| диаметральной плоскости с уравнением (11.1)=> 
, т.к. 
– координаты нормального вектора этой плоскости 
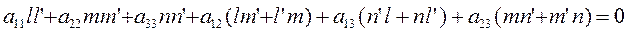(14) – условие того, что векторы 
и 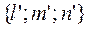имеют взаимно сопряженные направления относительно поверхности (2).
Главное направление и главная диаметральная
плоскость поверхности второго порядка
Определение. Направление 
называется главным направлением поверхности второго порядка, если оно перпендикулярно своей сопряженной диаметральной плоскости. При этом диаметральная плоскость, сопряженная главному направлению называется главной диаметральной плоскостью.
Утверждение. Главная диаметральная плоскость поверхности второго порядка является плоскостью симметрии этой поверхности.
Определение. Пересечение двух главных диаметральных плоскостей поверхности второго порядка образует ось симметрии поверхности, которая называется главной осью этой поверхности.
Пусть 
- главное направление => оно перпендикулярно своей диаметральной плоскости (11.1), а => || нормальному вектору плоскости (11.1) 
, значит
=> 
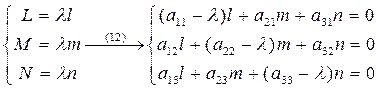(15) – условие того, что вектор имеет главное направление относительно поверхности (2).
(16) 
– условие того что система (15) имеет ненулевое решение => раскрыв определитель, получим
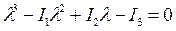(16.1)
Определение. Уравнение (16.1) называется характеристическим уравнением поверхности второго порядка; его корни называются характеристическими корнями этой поверхности.
Теорема Виета для уравнения третьей степени (16.1)
- уравнения главных диаметральных плоскостей i = 1,2,3.
Теорема. Центр центральной поверхности второго порядка находится в начале координат, тогда и только тогда, когда уравнение такой поверхности имеет вид:
Без доказательства.