Способ (решение с помощью обратной матрицы).

Негосударственное образовательное учреждение

Высшего профессионального образования

Волгоградский институт бизнеса

 

Математика

 

Задания и методические рекомендации по проведению

Домашней контрольной работы

 

Материалы допускаются к использованию в учебном процессе

 

Преподаватель __________ / ___________________

Заведующий кафедрой __________ / ___________________

«___»_____________ 2011г.

 

Преподаватель __________ / ___________________

Заведующий кафедрой __________ / ___________________

«___»_____________ 2012г.

 

Преподаватель __________ / ___________________

Заведующий кафедрой __________ / ___________________

«___»_____________ 2013г.

 

Преподаватель __________ / ___________________

Заведующий кафедрой __________ / ___________________

«___»_____________ 2014г.

 

Преподаватель __________ / ___________________

Заведующий кафедрой __________ / ___________________

«___»_____________ 2015г.

 

Задания и методические рекомендации по проведению домашней контрольной работы

Целью преподавания математических дисциплин студентам экономических специальностей является:

- ознакомление студентов с математическим аппаратом, необходимым для анализа процессов и явлений в ходе поиска оптимальных решений практических задач в экономических исследованиях;

- выработка умения самостоятельно изучать учебную литературу по математическим методам решения экономических задач;

- развитие логического мышления и повышение уровня математической культуры.

Правила выполнения контрольных работ

При выполнении контрольных работ надо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не засчитываются и возвращаются студенту для переработки.

1. Контрольную работу следует выполнять в тетради чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.

2. На обложке тетради должны быть ясно написаны фамилия, имя, отчество студента, учебный номер (шифр), номер контрольной работы, название дисциплины; здесь же следует указать дату отсылки работы в университет и адрес студента. В конце работы следует указать используемую литературу.

3. В работу должны быть включены все задачи, указанные в задании, строго по своему варианту. Контрольные работы, содержащие не все задачи, а также содержание задачи не своего варианта, не засчитываются.

4. Решение задач надо располагать в порядке номеров, указанных в задании, сохраняя номер задачи.

5. Перед решением каждой задачи надо выписывать полностью ее условие. В том случае, если несколько задач, из которых студент выбирает задачу своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить данные конкретными из соответствующего номера.

6. Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.

7. После получения прорецензированной работы, как недопущенной, так и допущенной к собеседованию, студент должен исправить все отмеченные рецензентом ошибки и недочеты, а также выполнить все рекомендации. Если рецензент предлагает внести в решение задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок. При высылаемых исправлениях должна обязательно находиться прорецензированная работа и рецензия на нее. В связи с этим рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для дополнений и исправлений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается.

8. По каждой работе проводится собеседование, после чего выставляется зачет по контрольной работе.

Вариант контрольной работы содержит 5 заданий. Задачи контрольной работы должны выбираться студентами по двум последним цифрам его учебного номера (шифра) в соответствии с таблицей выбора вариантов. В колонке в таблице по вертикали расположены цифры от 0 до 9, но каждая из них – последняя цифра личного шифра. Пересечения вертикальных (А) и горизонтальных (Б) линий определяют номера задач контрольной работы, записанные столбиком. Например, если личный шифр студента имеет две последние цифры 75, то он должен выполнить номера 3, 13, 23, 40, 49.

Таблица выбора вариантов домашней контрольной работы №1

Б А

Методические указания по выполнению заданий домашней контрольной работы № 1

Задача №1. Решить систему линейных алгебраических уравнений одним из трех способов:

1. методом Крамера,

2. с помощью обратной матрицы,

3. методом Гаусса. .

Способ (метод Крамера).

Формулы Крамера: ; ; , при ∆ ≠ 0.

15 – 1 – 8 – 4 – 10 – 3 = – 11.

25 – 0 – 6 – 3 – 0 – 5 = 11.

0 + 3 – 20 – 0 – 25 + 9 = – 33.

9 – 5 + 0 – 20 – 6 + 0 = – 22.

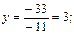; ; , при ∆ ≠ 0.

 

способ (решение с помощью обратной матрицы).

Перепишем систему уравнений в виде AX = B, где , , .

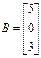Решение матричного уравнения имеет вид X = A^-1B. Найдем обратную матрицу A^-1. Имеем следующий главный определитель системы:

15 – 1 – 8 – 4 – 10 – 3 = – 11.

Вычислим алгебраические дополнения элементов этого определителя:

, , , , , , , , .

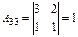Тогда обратная матрица имеет вид: , следовательно,

.

Ответ: x = –1; y = 3; z = 2.

 

Способ (метод Гаусса).

Составим расширенную матрицу системы и поменяем местами первую и вторую строки. Затем вычтем первую строку из второй и из третьей строк:

, .

 

Изменив знаки во второй строке и умножив ее на 5, прибавляем к третьей строке. Затем делим последнюю строку на 11:

. Теперь система уравнений принимает треугольный вид: .

Из последнего уравнения имеем z = 2; подставляя это значение во второе уравнение, получаем y = 3 и тогда из первого уравнения находим x = –1.

 

Задача №2. Построить прямую . Определить ее угловой коэффициент. Составить уравнения нескольких прямых, параллельных ей. Записать уравнение прямой, перпендикулярной к данной и проходящей через начало координат.

Преобразуем заданное уравнение – решим его относительно y, получим уравнение: . Отсюда угловой коэффициент прямой равен: - А/В = -(-4)/2 = 2.

Для построения прямой нужно знать координаты двух точек, удовлетворяющих ее уравнению. Задавая , получим . Задавая , получим . Значит, прямая проходит через точки А (0; 3) и В (-3/2; 0). Координаты точек, по которым строится график прямой, удобно записывать в таблицу:

 

x		3/2
y

 

Параллельные прямые имеют одинаковый угловой коэффициент, т.е. для заданной прямой параллельными, например, будут прямые: , , и т.д.

Произведение угловых коэффициентов параллельных прямых равно –1. Поэтому угловой коэффициент прямых, перпендикулярных заданной прямой, будет равен –1/2. Если прямая проходит через начало координат, то свободный член в уравнении такой прямой равен 0.

Тогда уравнение прямой, перпендикулярной к данной и проходящей через начало координат, будет иметь вид: .

Задача №3. Вычислить пределы:

а) .

Здесь предварительно имеем: 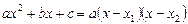, где и - корни квадратного трехчлена.

1) Числитель ; ; ; .

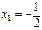2) Знаменатель ; ; ; .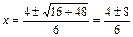

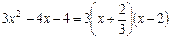б) , так как ; ; и при .

Задача №.4. Найти производные функций:

а) ; пользуясь правилами дифференцирования и таблицей производных, получим:

.

б) ; .

Задача №5. Выполним часть общего исследования функций:

Пример 1. Исследуем характер разрыва следующей функции 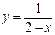имеет разрыв в точке , где она не определена. ; .

Односторонние пределы не существуют, следовательно, имеем разрыв второго рода. Через точку разрыва проходит вертикальная асимптота.

 

 

Пример 1. Найти экстремум функции .

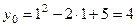Найдем производную . Приравниваем производную к нулю и находим критическую точку . Чтобы найти ординату этой точки, подставим в данную функцию и запишем вершину параболы C (1; 4). Ось симметрии проходит через C параллельно оси 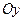(рис. 3). Пересечение параболы с осью 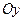: ; , т.е. A (0; 5). Симметричная ей точка A₁ (2; 5).

Пример 2. Найти точки экстремума функции и интервалы монотонности функции .

Находим первую производную: и приравниваем ее к нулю . Так как , то и . Критическая точка делит 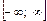на два интервала монотонности, при переходе через точку меняет знак с 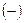на . Следовательно, - точка минимума.

 

Задача №6. Исследовать на экстремум функцию

Решение: находим частные производные функции ;

Критические точки функции находим из системы уравнений: . Находим: х = 4, у = -2

Следовательно, данная функция имеет одну критическую точку Р (4;-2)

Далее находим частные производные второго порядка и их значения в найденной критической точке

; ;

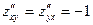
Частные производные второго порядка не содержат x, они постоянны в любой точке и, в частности, в точке Р (4;-2).

Имеем: А = -2; В = -1; С = -2

= 4-1 = 3>0. Так как Δ > 0 и А < 0, то в точке Р (4;-2) данная функция имеет максимум. Экстремум функции .

 

Задача №7

Пример 1. Решить дифференциальное уравнение и найти частное решение, удовлетворяющее начальному условию у (0) = 1.

Решение:

; Разделяем переменные 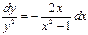. Интегрируем обе части последнего равенства

. В результате получим

Таким образом, получаем общий интеграл

Находим частное решение уравнения. Подставляем начальное условие , 1(0 + С) = 1; С = 1

Отсюда получаем частный интеграл

Пример 2. Найти общее решение дифференциального уравнения

и частное решение, удовлетворяющие начальному условию у (0) = 2.

Решение: Данное уравнение является линейным, так как содержит искомую функцию и ее производную в первой степени и не содержит их произведений. Применяем подстановку y = uv, где u и v – некоторые неизвестные функции аргумента х. Если y = uv, то . Подставляя у и в исходное уравнение, получим . Группируем первое и третье слагаемые и выносим v за скобку .

Так как искомая функция у представлена в виде произведения двух других неизвестных функций, то одну из них можно выбрать произвольно. Выберем функцию u так, чтобы выражение, стоящее в круглых скобках левой части равенства (1), обращалось в нуль, т.е., чтобы имело место равенство (2). Тогда уравнение (1) принимает вид (3).

Уравнение (2) является уравнением с разделяющимися переменными относительно u и x. Решим его

; ; ; .

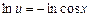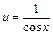Чтобы равенство (2) имело место, достаточно найти одно какое-либо частное решение, удовлетворяющее этому уравнению. Поэтому для простоты при интегрировании этого уравнения находим то частное решение, которое соответствует значению произвольной постоянной С = 0. Подставив в (3) найденное выражение для u, получим

; ; . Интегрируя, имеем

Теперь можно получить общее решение исходного уравнения

Определим значение произвольной постоянной С при указанных начальных условиях ; С = 2

Таким образом, есть частное решение, удовлетворяющее данному начальному условию.