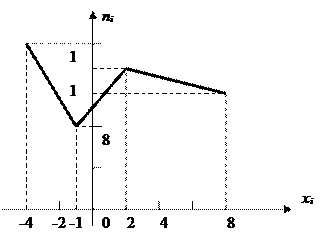Задачи №1-10. Решить систему линейных алгебраических уравнений одним из трех способов: 1) методом Крамера, 2) с помощью обратной матрицы, 3) методом Гаусса.
1)  2)
2)  3)
3)  4)
4) 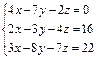 5)
5)  6)
6)  7)
7)  8)
8)  9)
9)  10)
10) 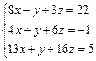
Задачи №11-20. Построить прямую  . Определить ее угловой коэффициент. Составить уравнения нескольких прямых, параллельных ей. Записать уравнение прямой, перпендикулярной к данной и проходящей через начало координат. Коэффициенты А, В, С заданы в таблице:
. Определить ее угловой коэффициент. Составить уравнения нескольких прямых, параллельных ей. Записать уравнение прямой, перпендикулярной к данной и проходящей через начало координат. Коэффициенты А, В, С заданы в таблице:
| Номер задачи | А | В | С |
| -2 | |||
| -6 | -2 | -10 | |
| -12 | |||
| -3 | |||
| -6 | -4 | ||
| -15 | |||
| -9 | |||
| -15 | |||
| -20 |
Задачи №21-30. Вычислить пределы:
21) а)  ; б)
; б)  . 22) а)
. 22) а)  ; б)
; б) 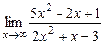 .
.
23) а)  ; б)
; б) 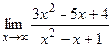 . 24) а)
. 24) а) 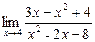 ; б)
; б)  .
.
25) а)  ; б)
; б) 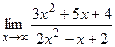 . 26) а)
. 26) а)  ; б)
; б)  .
.
27) а)  ; б)
; б)  . 28) а)
. 28) а)  ; б)
; б)  .
.
29) а)  ; б)
; б)  . 30) а)
. 30) а) 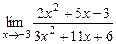 ; б)
; б) 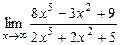 .
.
Задачи №31-40. Найти производные функций:
31) а)  ; б)
; б)  . 32) а)
. 32) а)  ; б)
; б)  .
.
33) а)  ; б)
; б)  . 34) а)
. 34) а)  ; б)
; б)  .
.
35) а)  ; б)
; б)  . 36) а)
. 36) а) 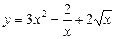 ; б)
; б)  .
.
37) а)  ; б)
; б)  . 38) а)
. 38) а)  ; б)
; б)  .
.
39) а)  ; б)
; б)  . 40) а)
. 40) а)  ; б)
; б)  .
.
Задачи №41-50. Выполнить исследование функции по следующей схеме:
1) найти область определения;
2) проверить четность-нечетность функции;
3) найти точки пересечения с осями координат;
4) найти экстремумы и интервалы монотонности;
5) найти точки перегиба и интервалы выпуклости и вогнутости;
6) найти пределы функции при 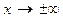 ;
;
7) построить график функции.
41)  . 42)
. 42)  . 43)
. 43)  . 44)
. 44)  .
.
45)  . 46)
. 46) 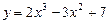 . 47)
. 47)  . 48)
. 48)  .
.
49)  . 50)
. 50)  .
.
Задачи №51-60. Исследовать на экстремум функцию двух переменных 
11) 
12) 
13) 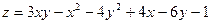
14) 
15) 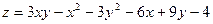
16) 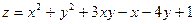
17) 
18) 
19) 
20) 
Задачи №61-70. Найти общее и частное решение дифференциального уравнения, удовлетворяющее начальным условием  при
при 
21)  у (0) = 1
у (0) = 1
22) 

23) 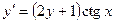

24) 

25) 

26)  у (0) = 3
у (0) = 3
27)  у (0) = 1
у (0) = 1
28) 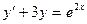

29)  у (0) = 1
у (0) = 1
30) 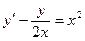 у (1) = 1
у (1) = 1
Таблица выбора вариантов домашней контрольной работы №2
| Б А | ||||||||||
Методические указания по выполнению заданий домашней контрольной работы № 2
Задача №1.
В партии из N изделий M бракованных. Из партии наугад выбирается n изделий. Определить вероятность того, что среди этих n изделий будет ровно m бракованных.
Решение. Задача решается с помощью классической формулы для вычисления вероятностей:
 .
.
Общее число возможных исходов равно числу сочетаний  . Число исходов, благоприятствующих появлению m бракованных изделий, равно
. Число исходов, благоприятствующих появлению m бракованных изделий, равно  . Отсюда вероятность интересующего нас события:
. Отсюда вероятность интересующего нас события:  .
.
Задача №2.
Имеются три одинаковые урны. В первой урне находятся 2 белых шара и 1 черный, во второй – 3 белых и 1 черный, в третьей – 2 белых и 2 черных шара. Выбрав наугад одну из урн, вынимают шар. Найти вероятность того, что этот шар белый.
Решение. Задача решается с помощью формулы полной вероятности:  .
.
В данной задаче возможны три гипотезы: А1 – выбрана первая урна, А2 – выбрана вторая урна, А3 – выбрана третья урна.
Событие А – появление белого шара. Так как гипотезы равновозможны, то 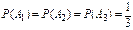 .
.
Условные вероятности события А при указанных гипотезах соответственно равны: 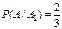 ,
,  ,
,  . (Так как в каждой урне общее число шаров двух цветов соответственно равно: три, четыре и два.)
. (Так как в каждой урне общее число шаров двух цветов соответственно равно: три, четыре и два.)
Подставив в формулу полной вероятности, получим ответ: 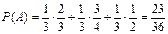 .
.
Задача №3.
Вероятность изготовления на автоматическом станке стандартной детали равна 0,9. Определить вероятность того, что из 6 наудачу взятых деталей 4 окажутся стандартными.
Решение. Условие задачи соответствует схеме повторных испытаний в одинаковых условиях. Поэтому задача решается с помощью формулы Бернулли:  ,
,
где число сочетаний равно:  . (n! =
. (n! =  ).
).
Применяя формулу Бернулли при n = 6, m = 4 и p = 0,9, получим:  .
.
Задача №4.
Случайная величина Х распределена по нормальному закону с математическим ожиданием, равным 6, и средним квадратическим отклонением, равным 2. Найти: 1) вероятность того, что в результате испытания Х примет значение из интервала (4; 8), и 2) вероятность того, что отклонение случайной величины от ее математического ожидания по абсолютной величине будет меньше 1,5.
Решение. Задача решается с помощью формул:  и
и  ,
,
где  - функция Лапласа, которая является нечетной, т.е.
- функция Лапласа, которая является нечетной, т.е.  , и вычисляется с помощью соответствующих таблиц (см. Список литературы).
, и вычисляется с помощью соответствующих таблиц (см. Список литературы).
Здесь a - математическое ожидание, s - среднее квадратическое отклонение. По условию a = 6, s = 2, a = 4, b = 8, d = 1,5. Тогда  и
и  .
.
Задача №5.
Задан закон распределения дискретной случайной величины Х:
| xi | |||
| pi | 0,5 | 0,2 | 0,3 |
Вычислить математическое ожидание, дисперсию и среднее квадратическое отклонение. Вычислить математическое ожидание и дисперсию случайной величины  .
.
Решение. Расчет ведем по формулам для числовых характеристик дискретных случайных величин.
Математическое ожидание: 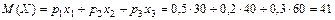 .
.
Дисперсия: 
Среднее квадратическое отклонение:  .
.
Для вычисления характеристик случайной величины  воспользуемся свойствами математического ожидания и дисперсии:
воспользуемся свойствами математического ожидания и дисперсии:  ,
,
 .
.
Задача №6.
Дана интегральная функция F(x) распределения непрерывной случайной величины:  .
.
Требуется: 1) убедиться, что заданная функция F(x) является функцией распределения, проверив свойства функции; 2) найти плотность данного распределения f(x); 3) построить графики интегральной и дифференциальной функций распределения.
Решение. 1) На левом конце участка  заданной функции имеем: F(1)=
заданной функции имеем: F(1)= 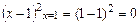 , а на правом конце участка: F(2)=
, а на правом конце участка: F(2)=  . Так как выполняется свойство непрерывности функции распределения, то F(x) является интегральной функцией распределения непрерывной случайной величины.
. Так как выполняется свойство непрерывности функции распределения, то F(x) является интегральной функцией распределения непрерывной случайной величины.
2) Плотность распределения или дифференциальная функция распределения непрерывной случайной величины находится по формуле:  , т.е. в данном случае:
, т.е. в данном случае: 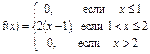 .
.
 3)
3)
Задача №7.
Рассчитать и построить гистограмму относительных частот по сгруппированным данным, где mi – частота попадания вариант в промежуток (хi, хi+1).
| i |  xi<X xi<X  xi+1 xi+1
| mi |
| 2 – 6 | ||
| 6 – 10 | ||
| 10 – 14 | ||
| 14 – 18 | ||
| 18 - 22 |
Решение. Относительная частота рассчитывается по формуле:  . Т.е. при 5+3+18+9+5=40 получим ряд значений:
. Т.е. при 5+3+18+9+5=40 получим ряд значений:
 ,
,  ,
,  ,
,  ,
,  .
.
По полученным результатам и данным таблицы строим гистограмму.

Задача №8.
На основании данного распределения выборки найти выборочное среднее, смещённую и несмещенную выборочные дисперсии. Построить полигон частот.
| Распределение | ||||
| хi | -4 | -1 | ||
| ni |
Решение. Найдём выборочное среднее (несмещенную оценку математического ожидания):
 .
.
Смещённая оценка дисперсии:  .
.
Несмещённая (исправленная) дисперсия:  . По данным таблицы строим полигон частот.
. По данным таблицы строим полигон частот.