Вычислить пределы:
а)  , б) , б)  ,
в) ,
в)  ,г) ,г)  . .
|
Решение:
а) Подстановка предельного значения аргумента х=-3 приводит к неопределенному выражению вида  .
.
Для устранения этой неопределенности разложим числитель и знаменатель дроби на множители и сократим дробь на множитель (х+3). Такое сокращение здесь возможно, так как множитель (х+3) отличен от нуля при х→ −3:

 .
.
б) При х → ∞ выражение  дает неопределенность вида (∞ − ∞). Для ее устранения умножим и разделим это выражение на
дает неопределенность вида (∞ − ∞). Для ее устранения умножим и разделим это выражение на 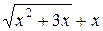 , после чего разделим числитель и знаменатель полученной дроби на х, учитывая формулу (25):
, после чего разделим числитель и знаменатель полученной дроби на х, учитывая формулу (25):
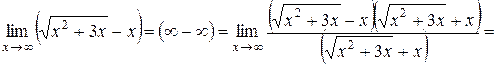
 .
.
в) При  получим неопределенность
получим неопределенность  . Обозначим arctg5x = y. Тогда 5х=tgy и y → 0 при х → 0. Применяя свойства пределов и формулу (26), имеем:
. Обозначим arctg5x = y. Тогда 5х=tgy и y → 0 при х → 0. Применяя свойства пределов и формулу (26), имеем:
 .
.
Эту задачу можно решить, используя эквивалентные замены бесконечно малых величин (28). Поскольку при  эквивалентны
эквивалентны  , можно записать
, можно записать
 .
.
г) При  выражение
выражение  является неопределенностью вида
является неопределенностью вида 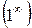 . Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой (при х → ∞) величины; после чего применим формулу второго замечательного предела (27):
. Для устранения этой неопределенности представим основание степени в виде суммы 1 и бесконечно малой (при х → ∞) величины; после чего применим формулу второго замечательного предела (27):


 .
.
Задача 6.
Теоретические сведения.
Производной от функции 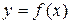 по аргументу x называется предел отношения приращения функции D у к приращению аргумента D х, когда последнее стремится к нулю:
по аргументу x называется предел отношения приращения функции D у к приращению аргумента D х, когда последнее стремится к нулю:
 .
.
Производная есть скорость изменения функции в точке х.
Отыскание производной называется дифференцированием функции.
Основные правила дифференцирования:
1.  , где C=Const.
, где C=Const.
2. 
3. 
4.  ,
, 
5.  ,
,  ,
, 
6. 
Таблица производных элементарных функций ( ):
):
1.  , 4.
, 4. 
2. 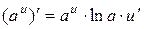 ,
,  , 5.
, 5. 
3.  , 6.
, 6.  , 7.
, 7. 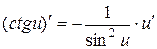 ,
,
8.  ,
, 
9.  ,
, 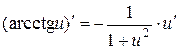
Если в таблице положить 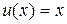 , то
, то  .
.
Пример выполнения задания.
Найдите производные функций:
а)  ; б) ; б)  ; в) ; в)  . .
|
Решение:
а) последовательно применяя правила дифференцирования сложной функции, правила и формулы дифференцирования, имеем:

 ;
;
б) 



в) в данном случае функциональная зависимость задана в неявном виде. Для нахождения производной  нужно продифференцировать по переменной х обе части уравнения, считая при этом у функцией от х, а затем полученное уравнение разрешить относительно
нужно продифференцировать по переменной х обе части уравнения, считая при этом у функцией от х, а затем полученное уравнение разрешить относительно  :
:
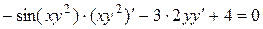 ;
;
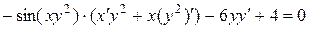 ;
;
 ;
;
 ;
;
Из последнего уравнения находим  :
:
 ;
;
 .
.
Задача 7.
Теоретические сведения. Исследование функции одной независимой переменной будем проводить по следующей схеме:
1. Найдем область определения функции.
2. Исследуем функцию на непрерывность.
3. Установим, является ли данная функция четной, нечетной или функцией общего вида.
4. Найдем интервалы возрастания и убывания функции, точки экстремума.
5. Найдем интервалы выпуклости и вогнутости кривой, точки ее перегиба.
6. Найдем асимптоты кривой.
Пример выполнения задания.
Исследовать функцию  и построить ее график. и построить ее график.
|
Решение.
Реализуем приведенную схему исследования функции:
1. Функция определена при всех значениях аргумента х, кроме х= 1.
2. Данная функция является элементарной, поэтому она непрерывна на своей области определения, то есть на интервалах  и
и  .
.
В точке х= 1 функция терпит разрыв.
3. Для установления четности или нечетности функции проверим выполнимость равенств  (тогда
(тогда  − четная функция) или
− четная функция) или  (для нечетной функции) для любых х из области определения функции:
(для нечетной функции) для любых х из области определения функции:  ,
,  .
.
Следовательно, 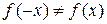 и
и  , то есть данная функция является функцией общего вида.
, то есть данная функция является функцией общего вида.
4. Для исследования функции на экстремум найдем ее первую производную:
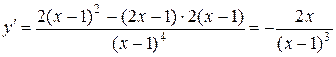 .
.
Определим критические точки функции:  при
при 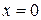 ,
,  не существует при
не существует при  . Тем самым имеем две критические точки: х= 0, х= 1. Но точка х= 1 не принадлежит области определения функции, экстремума в ней быть не может.
. Тем самым имеем две критические точки: х= 0, х= 1. Но точка х= 1 не принадлежит области определения функции, экстремума в ней быть не может.
Разобьем числовую ось на три интервала  ,
,  ,
,  .
.

В первом и третьем интервалах первая производная отрицательна, следовательно, здесь функция убывает, во втором интервале − положительна, и данная функция возрастает. При переходе через точку x =0 первая производная меняет свой знак с минуса на плюс, поэтому в этой точке функция имеет минимум: 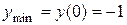 . Значит, А(0;−1) является точкой минимума.
. Значит, А(0;−1) является точкой минимума.
5. Для определения точек перегиба графика функции и интервалов выпуклости и вогнутости кривой найдем вторую производную:
 .
.
Для второй производной  при
при  и
и  не существует при х =1. Разобьем числовую ось на три интервала
не существует при х =1. Разобьем числовую ось на три интервала  ,
,  ,
,  .
.

На первом интервале вторая производная  отрицательна и дуга исследуемой кривой выпукла; на втором и третьем интервалах
отрицательна и дуга исследуемой кривой выпукла; на втором и третьем интервалах 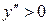 , поэтому график является вогнутым. При переходе через точку
, поэтому график является вогнутым. При переходе через точку  вторая производная меняет свой знак, поэтому в этой точке кривая имеет перегиб:
вторая производная меняет свой знак, поэтому в этой точке кривая имеет перегиб:  .
.
Следовательно,  − точка перегиба графика функции.
− точка перегиба графика функции.
6. В точке  функция терпит разрыв, причем
функция терпит разрыв, причем 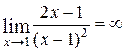 . Прямая
. Прямая  является вертикальной асимптотой графика функции. Для определения уравнения наклонной асимптоты
является вертикальной асимптотой графика функции. Для определения уравнения наклонной асимптоты  воспользуемся формулами:
воспользуемся формулами:
 ,
,  .
.
Тогда  ,
,  .
.
При найденных значениях k и b прямая  есть горизонтальная асимптота графика исследуемой функции, представленного на рисунке 1.
есть горизонтальная асимптота графика исследуемой функции, представленного на рисунке 1.
 | |||
 |
Рисунок 1. График исследуемой функции.
Задача 8.
Пример выполнения задания.
| Резервуар, имеющий форму открытого сверху прямоугольного параллелепипеда с квадратным дном, нужно вылудить внутри оловом. Каковы должны быть размеры резервуара при его емкости 108 дм3, чтобы затраты на его лужение были наименьшими? |
Решение. Затраты на покрытие резервуара оловом будут наименьшими, если при данной вместимости площадь его поверхности будет минимальной.
Обозначим через а (дм) − сторону основания, b (дм) − высоту резервуара. Тогда площадь его поверхности S =  , а объем
, а объем  , или, согласно условия,
, или, согласно условия,  . Поэтому
. Поэтому
 и
и 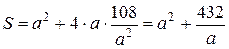 .
.
Полученное соотношение устанавливает зависимость между площадью поверхности резервуара S (функция) и стороной основания a (аргумент). Область определения этой функции  , так как а – сторона основания. Исследуем функцию S на экстремум. Найдем первую производную
, так как а – сторона основания. Исследуем функцию S на экстремум. Найдем первую производную  , приравняем ее к нулю и решим полученное уравнение:
, приравняем ее к нулю и решим полученное уравнение:
 .
.
Отсюда  . Производная
. Производная  не существует при
не существует при 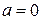 , но это значение аргумента не принадлежит области определения функции. При
, но это значение аргумента не принадлежит области определения функции. При 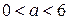 производная
производная 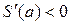 , при
, при 
 . Следовательно, при
. Следовательно, при  функция S имеет минимум. Если
функция S имеет минимум. Если  , то
, то  . Таким образом, затраты на лужение резервуара емкостью 108 л будут наименьшими, если он имеет размеры
. Таким образом, затраты на лужение резервуара емкостью 108 л будут наименьшими, если он имеет размеры  .
.
Задача 9.
Теоретические сведения.
Переменная величина z называется функцией двух переменных x и y, если каждой паре значений (x,y) из данной области соответствует единственное определенное значение  .
.
Для функции  вводятся понятия частных производных первого порядка, которые определяются выражениями:
вводятся понятия частных производных первого порядка, которые определяются выражениями:
 ,
,  ,
,
и частных производных второго порядка:
 ,
,  ,
,  .
.
Функция  имеет в точке
имеет в точке  максимум (минимум), если значение этой функции в точке
максимум (минимум), если значение этой функции в точке  больше (меньше), чем значения функции в любой точке из окрестности точки
больше (меньше), чем значения функции в любой точке из окрестности точки  .
.
Необходимыми условиями существования экстремума (максимума или минимума) дифференцируемой функции  является равенство нулю ее частных производных первого порядка:
является равенство нулю ее частных производных первого порядка:
 .
.
Точки, в которых частные производные обращаются в ноль, называются стационарными точками функции  . Для того чтобы стационарная точка являлась экстремумом, в ней должны выполняться достаточные условия. Обозначим
. Для того чтобы стационарная точка являлась экстремумом, в ней должны выполняться достаточные условия. Обозначим  ,
,  ,
,  ,
, 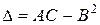 .
.
Если в стационарной точке 
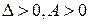 , то
, то  есть точка минимума;
есть точка минимума;
 , то
, то  есть точка максимума;
есть точка максимума;
 , то в точке
, то в точке  нет экстремума;
нет экстремума;
 , то требуется дополнительное исследование.
, то требуется дополнительное исследование.
Пример выполнения задания.
Исследовать на экстремум функцию  . .
|
Решение.
1. Найдем частные производные заданной функции
 ,
,  .
.
2. Запишем необходимые условия существования экстремума



 ,
,
значит точка  является стационарной точкой функции.
является стационарной точкой функции.
3. Проверим выполнение в точке М достаточного условия. Для этого найдем вторые частные производные функции
 ,
,  ,
,  .
.
В точке 
 и
и  . Поскольку
. Поскольку  , точка
, точка  является точкой максимума. Значение функции в этой точке
является точкой максимума. Значение функции в этой точке  .
.
Задача 10.
Теоретические сведения.
Функция двух независимых переменных  принимает наибольшее и наименьшее значения в области D, ограниченной линией
принимает наибольшее и наименьшее значения в области D, ограниченной линией  , либо в стационарных точках, расположенных внутри области D, либо на границе этой области.
, либо в стационарных точках, расположенных внутри области D, либо на границе этой области.
Задача об отыскании наибольшего и наименьшего значений функции  в заданной области D решается по следующему плану:
в заданной области D решается по следующему плану:
1. Определяем стационарные точки функции, расположенные внутри области D, и вычисляем значения функции в этих точках.
2. Находим стационарные точки функции на границе  области или на отдельных ее участках, заданных различными уравнениями, и вычисляем значения функции в этих точках.
области или на отдельных ее участках, заданных различными уравнениями, и вычисляем значения функции в этих точках.
3. Из всех вычисленных значений функции выбираем наибольшее и наименьшее.
Пример выполнения задания.
Найти наибольшее и наименьшее значения функции  в треугольнике, ограниченном прямыми в треугольнике, ограниченном прямыми 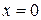 , ,  , ,  . .
|
Решение.
1. Найдем стационарные точки функции из условий равенства нулю частных производных функции
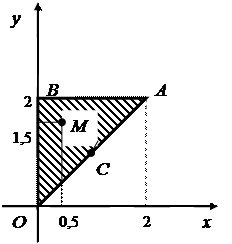



Стационарная точка  лежит внутри заданной области ОАВ.
лежит внутри заданной области ОАВ.
Значение функции в точке М равно
 .
.
2. Исследуем поведение функции на границах области:
а) на границе ОА  ,
,  ,
,  или
или  ;
;
 ,
,  при
при  , тогда
, тогда  (так как у=х).
(так как у=х).
В точке  значение функции равно
значение функции равно  .
.
Вычислим значения функции в крайних точках отрезка ОА.
В точке 
 , в точке
, в точке  значение функции равно
значение функции равно
 .
.
б) на границе ВА  ,
,  ,
,  или
или  ;
;
 ,
,  при
при 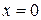 , а
, а  согласно уравнению прямой ВА.
согласно уравнению прямой ВА.
В точке  значение функции равно
значение функции равно  .
.
в) на границе ОВ 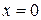 ,
,  ,
, 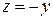 ;
;
 при всех
при всех  , следовательно, стационарных точек на
, следовательно, стационарных точек на
линии ОВ нет.
3. Из всех вычисленных значений заданной функции выбираем наибольшее и наименьшее:
 − наибольшее значение функции в области ОАВ
− наибольшее значение функции в области ОАВ
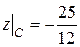 − наименьшее значение функции в области ОАВ
− наименьшее значение функции в области ОАВ