Теорема сложения вероятностей
Сформулируем теорему (правило) сложения вероятностей.
Теорема. Вероятность суммы несовместных событий равна сумме вероятностей этих событий:
 (1)
(1)
Докажем теорему для схемы случаев, рассматривая сумму двух событий. Пусть в результате испытания из общего числа п равновозможных и несовместных (элементарных) исходов испытания (случаев) событию А благоприятствует т 1 случаев, а событию В — т2 случаев (рис. 1).
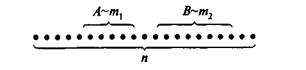
Рис 1
Согласно классическому определению Р(А] = m1/n Р(В] = m2/n.
Так как события А и В несовместные, то ни один из случаев, благоприятствующих одному из этих событий, не благоприятствует другому (см. рис. 1). Поэтому событию А+В будет благоприятствовать m1+m2 случаев. Следовательно,
P(A +B)= (m1+m2) / n (=P(A)+P(B).
Следствие 1. Сумма вероятностей событий, образующих полную группу, равна единице:
 (2)
(2)
Если события А,В,..:,К образуют полную группу, то они единственно возможные и несовместные.
Так как события А,В,...,К — единственно возможные, то событие А+В+...+К, состоящее в появлении в результате испытания хотя бы одного из этих событий, является достоверным, т.е. его вероятность равна единице:
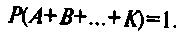
В силу того, что события А,Б,...,К — несовместные, к ним применима теорема сложения (1), т.е.

Следствие 2. Сумма вероятностей противоположных событий равна единице:
 (3)
(3)
О Утверждение (1.18) следует из того, что противоположные события образуют полную группу.
Пример 1. Вероятность выхода изделия из строя при эксплуатации сроком до одного года равна 0,13, а при эксплуатации сроком до 3 лет — 0,36. Найти вероятность выхода изделия из строя при эксплуатации сроком от 1 года до 3 лет.
Решение. Пусть события А, В, С — выход из строя изделий при эксплуатации сроком соответственно до 1 года, от 1 года до 3 лет, свыше 3 лет, причем по условию Р(С)=0,13, Р(С)=0,36. Очевидно, что С=А+В, где А и В — несовместные события. По теореме сложения Р(С)= Р(А)+Р(В), откуда Р(В)=Р(С) - Р(А)= 0,36 - 0,13 =0,23

В силу того, что события А,В,...,К — несовместные, к ним применима теорема сложения (1), т.е.

Условная вероятность события.
Как отмечено выше, вероятность Р(В) как мера степени объективной возможности наступления события В имеет смысл при выполнении определенного комплекса условий. При изменении условий вероятность события В может измениться. Так, если к комплексу условий, при котором изучалась вероятность Р(В), добавить новое условие А, то полученная вероятность события В, найденная при условии, что событие А произошло, называется условной вероятностью события В и обозначается РА(В) или Р(В/А).
Пример. В ящике 5 деталей, среди которых 3 стандартные и 2 бракованные. Поочередно из него извлекается по одной детали (с возвратом и без возврата). Найти вероятность извлечения во второй раз стандартной детали.
Решение. Пусть события А и В — извлечение стандартной детали соответственно в 1-й и 2-й раз. Очевидно, что Р(А) = 3/5. Если вынутая деталь вновь возвращается в ящик, то вероятность извлечения стандартной детали во второй раз Р(В) = 3/5. Если вынутая деталь в ящик не возвращается, то вероятность извлечения стандартной детали во второй раз Р(В) зависит от того, какая деталь была извлечена в первый раз - стандартная (событие А) или бракованная (событие А). В первом случае РА(В) = 2/4, во втором случае РА(В) = 3/4, так как из оставшихся четырех деталей стандартных будет соответственно 2 или 3. Найдем формулу для вычисления условной вероятности РА(В).
Пусть из общего числа n равновозможных и несовместных (элементарных) исходов испытания (случаев) событию А благоприятствует m случаев, событию В — k случаев, а совместному появлению событий А и В, т.е. событию АВ — l случаев (l < m, l < k) (см. рис.2).

Рис.2
Тогда согласно классическому определению вероятности

После того как событие А произошло, число всех равновозможных исходов (случаев) сократилось с n до m, а число случаев, благоприятствующих событию В, с k до l. Поэтому условная вероятность

Аналогично

Умножая правую и левую части равенств соответственно на Р(А) и Р(В), получим

Это так называемая теорема (правило) умножения вероятностей: вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие произошло.
Теорема (правило) умножения вероятностей легко обобщается на случай произвольного числа событий:

.т.е. вероятность произведения нескольких событии равна произведению вероятности одного из этих событий на условные вероятности других; при этом условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие события произошли.
Пример Работа электронного устройства прекратилась вследствие выхода из строя одного из пяти унифицированных блоков. Производится последовательная замена каждого блока новым до тех пор, пока устройство не начнет работать. Какова вероятность того, что придется заменить: а) 2 блока; б) 4 блока?
Решение. а) Обозначим события:
Аi — i- й блок исправен, i=1,2,...,5; В — замена двух блоков.
Очевидно, что придется заменить 2 блока, если 1-й блок исправен (4 шанса из 5), а 2-й —неисправен (1 шанс из оставшихся 4), т.е. B=A1  . Теперь по теореме умножения (1.21)
. Теперь по теореме умножения (1.21)

б) Пусть событие С — замена 4 блоков. Очевидно, что С = =A1 A2 A3  и по теореме умножения
и по теореме умножения

Теорема умножения вероятностей принимает наиболее простой вид, когда события, образующие произведение, независимы.
Событие В называется независимым от события А, если его вероятность не меняется от того, произошло событие А или нет. т.е.

В противном случае, если РА(В)¹Р(В) (или  ¹ Р(В)), событие В называется зависимым от А.
¹ Р(В)), событие В называется зависимым от А.
Докажем, что если событие В не зависит от А, то и событие А не зависит от В.
Так как по условию событие В не зависит от А. то

Запишем теорему умножения вероятностей в двух формах:

Заменяя РА(В) на Р(В), получим Р(А)•Р(В)= Р(В)РВ(А), откуда, полагая, что Р(В) ¹0, получим РВ(А)=Р(А), т.е. событие А не зависит от В.
Таким образом, зависимость и независимость событий всегда взаимны. Поэтому можно дать следующее определение независимости событий.
Два события называются независимыми, если появление одного из них не меняет вероятности наступления другого.
Несколько событий A,B,...,L называются независимыми в совокупности (или просто независимыми), если независимы любые два из них и независимы любое из данных событий и любые комбинации (произведения) остальных событий. В противном случае события A,B,...,L называются зависимыми.
Например, три события А, В, С независимы (независимы в совокупности), если независимы события А и В, А и С, В и С, А и ВС, В и АС, С и АВ.
Для независимых событий теорема (правило) умножения вероятностей для двух и нескольких событий примет вид:

т.е вероятность произведения двух или нескольких независимых событий равна произведению вероятностей этих событий.
Пример. Вероятность попадания в цель для первого стрелка равна 0,8, для второго—0,7, для третьего — 0,9. Каждый из стрелков делает по одному выстрелу. Какова вероятность того, что в мишени 3 пробоины?
Решение. Обозначим события:
Аi— попадание в цель i-го стрелка (i=1,2,3);
В — в мишени три пробоины.
Очевидно, что В = А1А2А3 причем события А1 А2 А3 — независимы. По теореме умножения для независимых событий
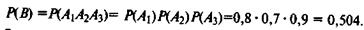
Замечание. Говоря о независимости событий, отметим следующее.
В основе независимости событий лежит их физическая независимость, означающая, что множества случайных факторов, приводящих к тому или иному исходу испытания, не пересекаются (или почти не пересекаются). Например, если в цехе имеются две установки, никак не связанные между собой по условиям производства, то простой каждой установки— события независимые. Если эти установки связаны единым технологическим циклом, то простой одной из установок зависит от состояния работы другой.
Вместе с тем, если множества случайных факторов пересекаются, то появляющиеся в результате испытания события не обязательно зависимые.
Пусть, например, рассматриваются события:
А — извлечение наудачу из колоды карты пиковой масти;
В — извлечение наудачу из колоды пикового туза.
Необходимо выяснить, являются ли события А и В зависимыми. На первый взгляд, можно предполагать зависимость событий А и В в силу пересечения случаев, им благоприятствующих: среди карт пиковой масти есть туз, а среди тузов — карта пиковой масти. Убедимся, однако, в том, что события А и В независимы.


При решении ряда задач требуется найти вероятность суммы двух или нескольких совместных событий, т.е. вероятность появления хотя бы одного из этих событий. В этом случае применять теорему сложения вероятностей нельзя.
Теорема. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их произведения. т.е.
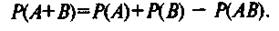
В справедливости данной формулы можно наглядно убедиться по рис. 3.

Рис.3
В случае трех и более совместных событий соответствующая формула для вероятности суммы Р(А+В+...+К) весьма громоздка и проще перейти к противоположному событию L:
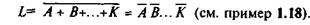
Тогда

те. вероятность суммы нескольких совместных событий А,В,...,К равна разности между единицей и вероятностью произведения противоположных событий А,В,...,К.
Если при этом события А, В,..,К —независимые, то

Пример На 100 лотерейных билетов приходится 5 выигрышных. Какова вероятность выигрыша хотя бы по одному билету, если приобретено: а) 2 билета; б) 4 билета?
Решение. Пусть событие А, — выигрыш по i-му билету i=1, 2, 3, 4).
а) Вероятность выигрыша хотя бы по одномy из двух билетов

б) Вероятность выигрыша хотя бы по одному из четырех билетов
