Система аксиом евклидовой геометрии.

Аксиоматический метод в геометрии.

Мыслитель Древней Греции Платон (428-348 гг. до н.э) и его ученик Аристотель (348-322 гг. до н.э) впервые сформулировали принципы построения всякой науки как аксиоматической теории.

В книге Евклида «Начала» геометрия была представлена как аксиоматическая теория, исходя из принципов, формулировки которых восходили к Платону и Аристотелю.

В книге «Основания геометрии» Д.Гильберт привёл полную систему аксиом евклидовой геометрии, доказал непротиворечивость этой системы аксиом и независимость некоторых аксиом от других аксиом системы.

Суть аксиоматического (дедуктивного) метода:

1. Выбирается ряд первоначальных понятий, которые не определяются и используются без объяснения их смысла.

2. Все другие используемые понятия должны быть строго определены через первоначальные понятия и через понятия, смысл которых был определён раньше.

Определение – высказывание, определяющее таким способом значение понятия.

Определяемое понятие – понятие, смысл которого определён.

Ситуация с утверждениями о первоначальных и определяемых понятиях аналогична (необходимо выделить некоторые утверждения и объявить их истинными).

Аксиома – утверждение, принимаемое без доказательства. Совокупность аксиом обозначим ∑.

Далее, пользуясь правилами логического умозаключения, выводятся новые утверждения о первоначальных и определяемых понятиях – теоремы.

Аксиоматическая теория (построенная на основе системы аксиом ∑) – совокупность всех теорем (), доказываемых, исходя из этой системы аксиом.

Система аксиом евклидовой геометрии.

В системе Гильберта первоначальными понятиями являются понятия трёх объектов: «точки», «прямые» и «плоскости» и трёх отношений между ними: «принадлежит», «между», «конгруэнтен». Точки обозначаются: A, B, C, …, прямые: a, b, c, …, плоскости: α, β, γ, …

Приведём двадцать аксиом, разделённых на пять групп.

I. Аксиомы принадлежности (или инцидентности)

(I.1) Для любых двух точек А, В существует единственная прямая, которой эти точки принадлежат. Эта прямая обозначается АВ.

(I.2) На прямой существуют по меньшей мере две точки.

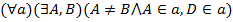
(I.3) Существуют три точки, не лежащие на одной прямой.

(I.4) Для любых трёх точек, не лежащих на одной и той же прямой, существует единственная плоскость, которой эти точки принадлежат.

Эта плоскость α обозначается (АВС).

(I.6) Если две точки прямой принадлежат плоскости, то всякая точка прямой принадлежит плоскости.

(I.7) Если две плоскости имеют общую точку, то они имеют по меньшей мере ещё одну общую точку.

(I.8) Существует по меньшей мере четыре точки, не принадлежащие одной плоскости.

(I.7) выражает факт, что пространство имеет не более трёх измерений, (I.8) – что пространство имеет не менее трёх измерений, (I.1)-(I.3) – плоскостные аксиомы группы I, (I.4)-(I.8) – пространственные аксиомы I группы.

II. Аксиомы порядка

Описывают свойства тернарного отношения мю «между» для точек. Если три точки A, B, C находятся в отношении «между», то – В лежит между точками А и С.

(II.1) Если точка В лежит между точкой А и точкой С, то А, В, С суть три различные точки прямой и В лежит также между точками С и А.

(II.2) Для любых двух точек А и В на прямой (АВ) существует точка С такая, что В лежит между А и С.

(II.3) Среди любых трёх точек прямой существует не более одной точки, лежащей между двумя другими.

Отрезком с концами А и В называется множество точек: [AB]={A,B} . Точки множества называются внутренними точками отрезка.

(II.4) (Аксиома Паша) Пусть А, В, С – три точки, не лежащие на одной прямой, и а – прямая в плоскости (АВС), не проходящая ни через одну из точек А,В,С. Тогда если прямая а проходит через внутреннюю точку отрезка [АВ], то она проходит также через внутреннюю точку отрезка [АС] или через внутреннюю точку отрезка [ВС].

Приведём ряд теорем, которые доказываются на основе аксиом I-II групп.

1. Для любых двух различных точек А и В на прямой (АВ) существует по меньшей мере одна точка, лежащая между А и В.

Доказательство (проверьте!!! На всякий случай.):

Согласно аксиоме (I.3) вне прямой (АВ) существует С , а в силу аксиомы (II.2) на (АС) существует D, что . В силу той же аксиомы (II.2) и (II.3) на (DB) существует G, что . Остаётся применить (II.4) к треугольнику АDB и (СG). На её основе существует М, в которой (СG) пересекает [AB] этого треугольника, т.е. .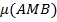

2. Среди трёх различных точек А, В, С на одной и той же прямой всегда существует одна точка, лежащая между двумя другими.

III. Аксиомы конгруэнтности

Описывают свойства отношения конгруэнтности для отрезков и отрезков углов ().

III.1 (Аксиома отложения отрезков) Если даны отрезок [АВ] и луч [OX), то существует точка такая, что .

III.2 Если два отрезка конгруэнтны третьему, то они конгруэнтны также друг другу.

III.3 (Аксиома сложения отрезков) Если .

III.4 (Аксиома отложения углов) Каждый угол может быть отложен единственным способом от данного луча в данной полуплоскости. Точнее, если даны (выпуклый) угол , луч 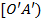и полуплоскость , ограниченная прямой , то в полуплоскости существует один и только один луч такой, что 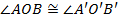. Кроме того, .

III.5 Если для любых двух треугольников АВС и имеют место конгруэнтности , то имеет место также и конгруэнтность .

Аксиомы третьей группы позволяют ввести понятие движения.

IV. Аксиомы непрерывности

(IV.1) (Аксиома Архимеда) Пусть даны отрезки [АВ] [CD]. Тогда на прямой (АВ) существует конечное множество точек , удовлетворяющих условиям:

а) ,

б) ,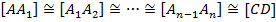

в) .

(IV.2) (Аксиома Кантора) Пусть на прямой а дана бесконечная последовательность отрезков [A₁B₁], [А₂В₂], …, удовлетворяющая двум условиям:

а) [A₁B₁] [А₂В₂] …,

б) для любого наперёд заданного отрезка [CD] найдётся натуральное число n такое, что [A_nB_n]<[CD].

Тогда на прямой а существует точка М, принадлежащая каждому из отрезков последовательности. Аксиомы непрерывности позволяют обосновать процесс измерения отрезков.

Аксиома Кантора требуется для того, чтобы доказать, что каково бы ни было вещественное число а>0 существует отрезок, длина которого равна а, а также соответствующую теорему для измерения углов: если при некотором выборе единицы измерения прямой угол имеет величину , то для каждого вещественного числа существует угол, величина которого равна .

Опираясь на аксиомы I-IV групп, можно ввести декартовы координаты на прямой, на плоскости и в пространстве.

V. Аксиома параллельности Евклида

V.1 Пусть а – произвольная прямая и А – точка, лежащая вне прямой а; тогда в плоскости, определяемой точкой А и прямой а, существует не более одной прямой, проходящей через точку А и не пересекающей прямой а.

Эта аксиома предназначена для обоснования евклидовой теории параллельных прямых. Две прямые, лежащие в одной плоскости и не имеющие общей точи, называются параллельными.

Её непротиворечивость.

Аксиоматическая теория называется непротиворечивой, если ни для какого утверждения А, сформулированного в терминах этой теории, само утверждение А и его отрицание не могут быть одновременно теоремами этой теории. В противном случае аксиоматическая теория называется противоречивой. Для доказательства непротиворечивости системы аксиом Гильберта построим модель этой системы аксиом в теории действительных чисел и тем самым докажем, что евклидова геометрия непротиворечива, если непротиворечива теория действительных чисел. Модель носит разные названия: числовая, арифметическая, аналитическая, координатная, декартова. Под точкой в модели будем понимать упорядоченную пару действительных чисел. Под прямой упорядоченную тройку вещественных чисел, из которых . Покажем, например, как доказывается выполнимость аксиом (I.1) и (V.1).

(I.1) Пусть A(x₁,y₁) и B(x₂,y₂) – две различные точки, т.е. x₁≠x₂ или y₁≠y₂. Покажем, что существует единственная прямая (a,b,c) проходящая через обе точки. Принадлежность точек А и В этой прямой означает, что должны быть выполнены равенства:

Вычтя почленно из первого уравнения второе, получим . Считая, например, что x₁≠x₂, находим отсюда 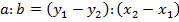. Положим . Подставим в первое уравнение системы и получим: . Следовательно, . Это и есть единственная прямая, проходящая через точки А и В. Если – произвольная точка, принадлежащая рассмотренной прямой, проходящей через точки A(x₁,y₁) и B(x₂,y₂), то . Эти соотношения нетрудно преобразовать к соотношению: . Обозначив каждое из этих отношений через t, получим, что все точки прямой (АВ) определяются двумя параметрическими уравнениями:

где, . Отметим, что точке А отвечает значение параметра , а точке В – значение .

Евклидова геометрия, построенная на базе системы аксиом Гильберта. Непротиворечива, если непротиворечива теория действительных чисел.