Тренды в данных могут привести к ложным корреляциям, следствием которых, являются ложные связи между переменными в регрессионном уравнении. В то же время, на самом деле, коррелируют между собой только временные тренды.
Временной тренд может быть исключен из результирующей переменной путем построения регрессии этой переменной по времени и перехода к остаткам, которые образуют новую стационарную переменную уже свободную от тренда. Или этот тренд может быть сразу включен в модель, путем введения времени в качестве одной из переменных-регрессоров. При этом используются регрессионные модели, основанные на стандартных t и F- тестах и оперирующие со стационарными временными рядами, имеющими постоянные средние и дисперсии.
При построении регрессии нестационарной переменной на детерминированную переменную времени, остатки обычно не дают в результате стационарную переменную.
Например, рассмотрим два процесса случайного блуждания
yt = yt-1 + ut, ut ~ IN(0,1), (12.1)
xt= xt-1 + vt, vt ~ IN(0,1), (12.2)
где IN(0,1) – класс временных рядов с независимыми приращениями с нулевым средним и единичной дисперсией, подчиняющимися нормальному закону.
Оба процесса представляют некоррелированные нестационарные переменные. Поэтому, если оценивается регрессионная модель
yt = b0 +b1 xt+et (12.3)
то, естественно за нулевую гипотезу H0 принять: H0: b1 = 0 и ожидать, что коэффициент детерминации R2, будет близок к нулю. Однако нестационарная природа данных влечет, что et также нестационарно. Отсюда, любая тенденция к росту в обоих рядах ведет к появлению корреляции, которая и будет отражена в регрессионный модели. Хотя, каждый ряд растет по совершенно разным причинам с некоррелированными уровнями роста (это значит, что в уравнении
D yt = a0 + a1Dxt+ht
коэффициент a1 сходится по вероятности к нулю). Итак, корреляция между нестационарными рядами еще не означает наличие существенных (причинных) связей между ними, как это выводится в случае стационарных рядов.
Кроме того, проблема кажущейся, ложной корреляции, выражающаяся в ненулевой оценке коэффициента b1, осложняется тем, что обычные выборочные t и F - статистики не имеют стандартных распределений, как в случае стационарных рядов. Существует явная тенденция к отрицанию гипотезы H0: b1 = 0 и такая тенденция возрастает с объемом выборки. Были проведены по методу Монте-Карло следующие эксперименты. Уравнение (12.3) было оценено десять тысяч раз, при этом yt и xt определялись по уравнениям (12.1) и (12.2). В результате оценок, среднее значение b1 оказалось равным -0.012 и соответствующая стандартная ошибка равна 0.006 (при размере выборки Т=100). Это дает отрицание гипотезы:H0: b1 = 0. Основываясь на 10000 повторений, вероятность отрицания H0 при уровне значимости 0.05 равна 0.753 (то есть, для 75,3% регрессий были получены значения t -статистики с |t|> 1.96). Это случилось из-за того, что средняя t-статистика полученная в эксперименте равна -0.12 с соответствующим стандартным отклонением 7.3. Нестандартное распределение t -статистики привело к очень высокой вероятности отрицания гипотезы H0.
Итак, заключаем, что часто возникает проблема ошибочного обнаружения связей в несвязанных между собой нестационарных временных рядах. Эта проблема возрастает с ростом выборки и не может быть разрешена попытками выделить тренды в изучаемых рядах, как это было возможно для стационарных рядов с временным трендом. Мы приходим к задаче: когда же можно делать вывод о причинной долговременной связи между нестационарными рядами, основываясь на регрессионном уравнении (12.3)?
Подход к решению этой проблемы - идея коинтеграции нестационарных временных рядов.
Говорят, что ряд содержит единичные корни и интегрируем с порядком d, то есть принадлежит классу I(d), если ряд становится стационарным после взятия d раз операции вычисления разности от временного ряда. В общем случае, любая линейная комбинация рядов класса I(d) должна также принадлежать I(d). Если, однако, существует вектор b, такой, что вектор возмущений ut = yt - bxt имеет меньший порядок интеграции I(d-b), где b > 0, то Энгл и Грангер (Engl and Granger (1987), [27]) определили, что yt и xt коинтегрированы с порядком (d, b). Если yt Î I(1) и xt Î I(1), а ut Î I(0), то оба ряда коинтегрированы с порядком CI(1,1).
С экономической точки зрения, если два или более ряда коинтегрированы, то существует между ними равновесная устойчивая долговременная связь, хотя сами ряды содержат стохастические тренды (не стационарны). Концепция коинтеграции может быть интерпретирована как существование долговременного устойчивого равновесного соотношения между параметрами экономической системы, а et (см. (12.3)) означает расстояние (ошибку) от равновесного направления в пространстве состояний (yt, xt).
12.2. Краткосрочные модели, коинтеграция и механизм корректировки ошибок.
Даже если можно прямо получить долгосрочную модель, имеет смысл рассмотреть краткосрочную эволюцию переменных при стремлении к долгосрочному состоянию. И это становится необходимым, если не удается обнаружить долгосрочные связи между переменными. В краткосрочных моделях можно использовать экономическую информацию, полученную в результате корректировки, регулирования процесса в целях улучшения прогноза в желаемом направлении.
Основная причина, почему связи не всегда находятся в точке равновесия, состоит в том, что экономические агенты не могут мгновенно приспособиться к новой информации. Часто текущее значение зависимой переменной Y определяется не только текущим значением объясняющей переменной X, но также и прошлыми значениями X. В динамическую модель могут входить и прошлые значения самой зависимой переменной Y. Это введение упрощает форму динамической модели, в противном случае в модель пришлось бы вводить большое число сильно коррелированных прошлых (с лагом) значений X.
Одной из простых динамических краткосрочных моделей является уравнение:
yt =a0 + g0 xt + g1 xt-1 + a1 yt-1 + ut , (12.4)
где ut - белый шум остатков, то есть ut ~ IN(0, s2). Ясно, что параметр g0 отражает краткосрочную реакцию yt на изменение xt, но не долгосрочный эффект, который присутствует в модели, находящейся в состоянии равновесия
yt = b0 +b1 xt. (12.5)
Поэтому в долгосрочной модели, эластичность между Y и X равна
b1 = (g0 + g1)/(1 - a1),
в предположении, что a1 < 1. (Это условие необходимо, если краткосрочная модель сходится к долгосрочной).
Динамическая модель (12.4) может быть легко усложнена (и часто она при этом становится более реалистичной), если увеличить число запаздываний по y, то есть параметр p и число запаздываний по x, то есть параметр q. Однако существует ряд трудностей при работе с моделями такого вида. Во-первых, как отмечалось, существует опасность высокой корреляции между текущими и прошлыми значениями переменных, которая создает проблему мультиколлинеарности (высокий R2, но неточная оценка параметров и малые значения t -статистик в модели, хотя форма и число переменных в модели может быть правильно определено).
Поэтому последовательное исключение незначащих переменных может привести к ошибочной спецификации модели (особенно в случае, когда X - векторная переменная). Кроме того, многие, если не все, переменные входящие в модель, могут быть нестационарными. Это ведет к потенциальной опасности ложной регрессии, так как в этом случае t и F- статистики не подчинены стандартным распределениям, и обычные выводы на их основе являются неверными.
Альтернативой может стать построение динамической модели в разностях. Правда, при этом теряется долгосрочная информация модели, что нежелательно при использовании модели в прогностических целях на долгий период.
Более удобный подход - это применение механизма корректировки ошибок (МКО) динамической модели.
Преобразуем уравнение (12.4) к виду
D yt = g0Dxt - (1 - a1)(yt-1- b0 - b1xt-1) + ut, (12.6)
где b0 = a0/(1- a1).
Уравнения (12.6) и (12.4) эквивалентны, но модель МКО(6) имеет несколько серьезных преимуществ. Первое, предполагая, что X и Y коинтегрированы, (МКО) сочетает краткосрочный и долгосрочный эффекты. Это может быть видно из того, что при достижении долгосрочного равновесия уравнение (12.6) переходит в уравнение равновесия (12.5).
Итак, если в какой то момент достигается равновесие, то
yt-1- b0 - b1xt-1 =0.
В течение неравновесного периода выражение в левой части последнего равенства ненулевое и измеряет расстояние от текущего положения системы до точки равновесия. Оценка параметра (1- а1) дает информацию о скорости контроля, то есть о том, с какой скоростью проходит изменение yt, в зависимости от расстояния от положения равновесия. (Большие значения, близкие к 1, величины (1-а1) свидетельствуют о том, что экономические факторы (так как в модели участвуют обычно логарифмы натуральных выражений) сильно изменяют результат, если система далека от равновесия. Малые значения (1 - а1) предполагают, что контроль и достижение долговременной стабилизации происходит медленно, возможно ввиду высокой стоимости затрат на регулирование (в денежном и неденежном смысле). Предположим, что переменная yt начала увеличиваться не так быстро, как это заложено в уравнении (12.5), возможно потому, что случилось большое отрицательное случайное колебание ut. В этом случае,
yt-1- b0 - b1xt-1 < 0, так как yt-1 растёт медленнее b0 + b1xt-1, но так как
- (1-а1) отрицательное, то в результате произойдёт увеличение D yt и yt возвращается назад по направлению к стабильному пути определённому уравнением (12.5).
Второй чертой МКО является тот факт, что все члены в модели стационарные, поэтому остаётся справедливой стандартная регрессионная техника исследований, предполагающая проверку коинтеграции по критерию Дики-Фулера (эти методы в пособие не вошли) и оценку коэффициентов b0 и b1. Часто b1 полагают единицей (b0 полагают равным нулю) и идет проверка такой долговременной эластичности.
В третьих, ясно, что МКО весьма близок к идее коинтеграции. И действительно, Энгл и Грангер ((1987) [28 ] показали, что если yt и xt коинтегрированы CI(1,1), тогда существует МКО и обратно, то есть МКО генерирует коинтегрированные ряды. Практически результаты Энгла и Грангера доказывают, что МКО обладают иммунитетом к ложной регрессии, благодаря тому, что хотя в уравнении присутствуют не преобразованные ряды, но они коинтегрированы с некоторым стационарным рядом.
Отметим, что возможны обобщения и усложнения уравнения (12.6). В общем случае можно задать МКО в виде
A(L) D yt = B(L)Dxt + (1 - p)(yt-p- b0 - b1xt-p) + ut, (12.7)
где A(L) - 1 -a1 L -a2 L2 -... - apLp полиномиальный лаг-оператор, B(L) - g0+ g1L + g2 L2 +... +gq Lq полиномиальный лаг-оператор, L -лаг, оператор запаздывания
L yt = yt-1, L xt = xt-1 и p = a1 +a2 +... +ap.
Наконец, возможно определение МКО в случае многих переменных, используя множество коинтегрированных векторов.
Контрольные вопросы к главе 12.
1. Объясните причины возникновения ложной корреляции, то есть корреляцией не вызванной непосредственной связью между факторами, в нестационарном случае.
2. Как записать долгосрочную и краткосрочную модели связи между факторами?
3. Какие соотношения между временными рядами должны выполняться в случае их коинтеграции?
4. Как получить модели, учитывающие как долгосрочные связи между факторами, так и краткосрочные изменения временного ряда под воздействием случайных отклонений (модели корректировки ошибок – МКО)?
5. Почему можно предполагать, что в моделях корректировки ошибок, устанавливающих связи между коинтегрированными временными рядами, ложная корреляция между факторами отсутствует?
Приложение 1.
Элементы линейной алгебры: основные понятия и факты.
Краткий обзор основных понятий линейной алгебры и аппарата матричного исчисления, использующих в эконометрических моделях, следует рассматривать как вспомогательный справочный материал, владение которым необходимо для успешного освоения дисциплины. Это Приложение ни в коей мере не может подменить полноценные учебники по этим вопросам. В своем изложении мы стремились следовать терминологии и обозначениям таких фундаментальных работ, как [7], [10], [20].
Векторное пространство.
В отличие от традиционных курсов мы не будем использовать определение векторного пространства как некоторого множества объектов, на котором выполняются некоторые аксиомы. Вместо этого определим сразу n -мерные векторы как столбцы, состоящие из n вещественных чисел, записанных в определённом порядке, и которые будем в дальнейшем обозначать следующим образом
Действительные числа 
называются координатами (компонентами) вектора 
.
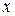Два вектора 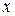и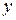 
называются равными, если равны их соответствующие координаты
.
Для заданных в такой форме векторов определены две линейные операции:
· операция сложения, которая выполняются в следующем виде
,
· и произведение вектора 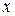на действительное число 
.
При этом предполагается, что справедливы следующие аксиомы, характеризующие свойства векторного пространства:
1. коммутативность сложения 
;
2. коммутативность произведения 
;
3. ассоциативность сложения 
;
4. ассоциативность произведения 
;
5. дистрибутивность умножения относительно сложения
;
6. дистрибутивность 
;
7. наличие нулевого вектора 0, такого, что 
для любого ;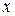
8. 
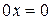для любого ;
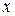9. 
для любого .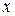
Множество всех n -мерных векторов с определёнными на нём операциями сложения и умножения на действительное число называется n -мерным векторным пространством и обозначается 
.
Линейной комбинацией векторов 
в пространстве называется выражение вида
Система векторов 
называется линейно независимой, если равенство
(П1.1)
выполняется только в том случае, когда все 
равны нулю. Если же существует набор коэффициентов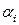 
, в котором хотя бы одно значение коэффициента отлично от нуля, при котором выполняется равенство П1.1, то такая система называется линейно зависимой. В случае линейной зависимости системы любой из её векторов может быть представлен в виде линейной комбинации остальных.
Совокупность линейно независимых векторов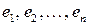 
называется базисом пространства , если любой вектор этого пространства 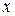может быть представлен в виде линейной комбинации этих векторов, т.е.
. (П1.2)
При этом равенство П1.2 называется разложением вектора 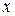по базису 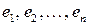, а числа 
координатами вектора в указанном базисе.
Наиболее важными являются следующие утверждения:
· Любой базис n - мерного векторного пространства содержит ровно n векторов. Число векторов, образующих базис, называется размерностью векторного пространства и обозначается 
.
· Любой вектор n - мерного векторного пространства единственным образом раскладывается по заданному базису.
Следствием первого утверждения является тот факт, что в любая система, состоящая из 
векторов, является линейно зависимой.
Некоторое подмножество 
линейного пространства называется линейным подпространством (или просто подпространством), если:
1. из 
следует, что 
для любых 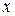и ;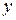
2. из 
следует, что 
при любом вещественном .
Очевидно, что 
.
Совокупность всех линейных комбинаций векторов называется линейной оболочкой этих векторов.
В эконометрических моделях понятие вектора и векторного пространства являются необходимыми при рассмотрении организации исходных данных. Понятие линейной зависимости (линейной комбинации) составляют основу линейных регрессионных моделей. Ортогональность базисных переменных в значительной степени связана с интерпретацией их независимости в случае нормального распределения.