Линейные операции над векторами

Контрольная работа

по дисциплине «Алгебра и геометрия»

Тема «Свободные векторы и операции над ними»

 

Выполнил:

студент I курса

Группы ИЗС-12

 

Проверил: преподаватель

Пыжьянова А.Н.

 

Нижний Новгород

Свободные векторы и операции над ними

Величины, которые полностью определяются своим численным значением, называются скалярными. Примерами скалярных величин являются: площадь, длина, объем, температура, работа, масса.

Другие величины, например сила, скорость, ускорение, определя­ются не только своим числовым значением, но и направлением. Такие величины называют векторными. Векторная величина геометрически изображается с помощью вектора.

Свободный вектор — класс эквивалентности, состоящий из множества равных направленных отрезков. Каждый направленный отрезок из этого класса является его представителем. Операции над свободными векторами производится через операции над их представителями.

Направленный вектор — это направленный прямолинейный отрезок, т. е. отре­зок, имеющий определенную длину и определенное направление. Если А — начало вектора, а В — его конец, то вектор обозначается символом АВ или а. Вектор ВА (у него начало в точке В, а конец в точке А) называется противоположным вектору АВ. Вектор, про­тивоположный вектору а, обозначается —а.

Длиной или модулем вектора АВ называется длина отрезка и обо­значается \АВ\. Вектор, длина которого равна нулю, называется нуле­вым вектором и обозначается 0. Нулевой вектор направления не имеет.

Вектор, длина которого равна единице, называется единичным век­тором и обозначается через ё. Единичный вектор, направление которо­го совпадает с направлением вектора а, называется ортом вектора а и обозначается а °.

Векторы а и b называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают а || 6. Коллинеарные векторы могут быть направлены одинаково или противоположно.

Нулевой вектор считается коллинеарным любому вектору. Два вектора а и b называются равными (а = 6), если они коллинеарные, одинаково направлены и имеют одинаковые длины. Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в лю­бую точку О пространства.

 

На рисунке векторы образуют прямоугольник. Справедливо равенство b = d, но а / / с. Векторы а и с — противоположные, а = —с.

 

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарные, то такие векторы компланарны.

Линейные операции над векторами

 

Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.

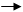
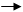
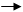
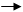
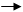
Пусть а и b — два произвольных вектора. Возьмем произволь­ную точку О и построим вектор OA = а. От точки А отложим вектор АВ = b,. Вектор ОВ, соединяющий начало первого вектора с концом второго, называется суммой векторов а и b: ОВ = а + b.

 

Это правило сложения векторов называют правилом треугольника. Сумму двух векторов можно построить также по правилу паралле­лограмма.

 

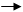
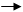
Под разностью векторов а и b понимается вектор с = а — b такой, что b + с — а.

Отметим, что в параллелограмме, построенном на векторах а и b, одна направленная диагональ является суммой векторов а и b, а другая — разностью.

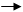
Можно вычитать векторы по правилу: а — b = а + (—b), т. е. вычи­тание векторов заменить сложением вектора а с вектором, противопо­ложным вектору b.

Произведением вектора а на скаляр (число) называется вектор • а (или а • ), который имеет длину | | = |а|, коллинеарен вектору а, имеет направление вектора а, если > 0 и противоположное направление, если < 0. Например, если дан вектор то векторы 3а и —2а будут иметь вид и .

Из определения произведения вектора на число следуют свойства этого произведения:

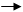
1. если b = - а, то b || а. Наоборот, если b || а, (а 0), то при некотором верно равенство b = а;

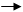
2. 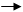всегда а = |а| • а0, т. е. каждый вектор равен произведению его модуля на орт.

 

Линейные операции над векторами обладают следующими свой­ствами:

 

Эти свойства позволяют проводить преобразования в линейных операциях с вектором так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные общие множители.

Существует два метода выполнения математических операций над векторами. В первом из них операции выполняются непосредственно над векторами, не связывая их с системой координат. По этой причине метод называется бескоординатным. Второй метод называется координатным. В этом методе математические операции производят не непосредственно над векторами, а над скалярными величинами, определяющими вектор в некоторой координатной системе.

 

Произведения векторов.

 

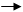
Скалярным произведением двух векторов назы­вается число, равное произведению длин этих векторов на косинус угла между ними. Если хоть один из векторов нулевой, то угол не определен, и скалярное произведение по определению равно нулю.

Скалярным произведением векторов a и b (обозначается ab) называют скаляр, определяемый равенством:

 

где — угол между векторами a и b, приведенными к общему началу

 

 

 

Скалярное произведение векторов обладает следующими свойствами:

 

Скалярное произведение векторов и в координатах вычисляется по формуле:

 

 

 

Векторное произведение векторов обладает свойствами:

Литература

1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Физматлит, 2003.

2. Конспект лекций по высшей математике/ Письменный Т.Д. М. 2009.

3. Материалы по геометрии: Элементы векторной алгебры / Сост. С.Е. Антонова, О.В. Казнина. – Н.Новгород: НГПУ, 2002.

4. Степанов Н.А., Жогова Т.Б., Казнина О.В. Геометрия I: Учеб. пособие для студентов – Н.Новгород: НГПУ, 2007.