Частное образовательное учреждение высшего образования
Волгоградский институт бизнеса
Экономико-математические методы и модели
Задания и методические рекомендации по проведению
Домашней контрольной работы
Материалы допускаются к использованию в учебном процессе
Преподаватель __________ / ___________________
Заведующий кафедрой __________ / ___________________
«___»_____________ _____ г.
Преподаватель __________ / ___________________
Заведующий кафедрой __________ / ___________________
«___»_____________ _____ г.
Преподаватель __________ / ___________________
Заведующий кафедрой __________ / ___________________
«___»_____________ _____ г.
Преподаватель __________ / ___________________
Заведующий кафедрой __________ / ___________________
«___»_____________ _____ г.
Преподаватель __________ / ___________________
Заведующий кафедрой __________ / ___________________
«___»_____________ _____ г.
Правила выполнения контрольной работы
При выполнении контрольных работ надо строго придерживаться указанных ниже правил. Работы, выполненные без соблюдения этих правил, не засчитываются и возвращаются обучающемуся для переработки.
1. Контрольную работу следует выполнять в тетради чернилами любого цвета, кроме красного, оставляя поля для замечаний рецензента.
2. На обложке тетради должны быть ясно написаны фамилия, имя, отчество обучающегося, учебный номер (шифр), номер контрольной работы, название дисциплины; здесь же следует указать дату отсылки работы в университет и адрес обучающегося. В конце работы следует указать используемую литературу.
3. В работу должны быть включены все задачи, указанные в задании, строго по своему варианту. Контрольные работы, содержащие не все задачи, а также содержание задачи не своего варианта, не засчитываются.
4. Решение задач надо располагать в порядке номеров, указанных в задании, сохраняя номер задачи.
5. Перед решением каждой задачи надо выписывать полностью ее условие. В том случае, если несколько задач, из которых обучающийся выбирает задачу своего варианта, имеют общую формулировку, следует, переписывая условие задачи, заменить данные конкретными из соответствующего номера.
6. Решение задач следует излагать подробно и аккуратно, объясняя и мотивируя все действия по ходу решения и делая необходимые чертежи.
7. После получения прорецензированной работы, как недопущенной, так и допущенной к собеседованию, обучающийся должен исправить все отмеченные рецензентом ошибки и недочеты, а также выполнить все рекомендации. Если рецензент предлагает внести в решение задач те или иные исправления или дополнения и прислать их для повторной проверки, то это следует сделать в короткий срок. При высылаемых исправлениях должна обязательно находиться прорецензированная работа и рецензия на нее. В связи с этим рекомендуется при выполнении контрольной работы оставлять в конце тетради несколько чистых листов для дополнений и исправлений в соответствии с указаниями рецензента. Вносить исправления в сам текст работы после ее рецензирования запрещается.
8. По каждой работе проводится собеседование, после чего выставляется зачет по контрольной работе.
Вариант контрольной работы содержит 5 заданий. Задачи контрольной работы должны выбираться обучающимися по двум последним цифрам его учебного номера (шифра) в соответствии с таблицей выбора вариантов. В колонке в таблице по вертикали расположены цифры от 0 до 9, но каждая из них – последняя цифра личного шифра. Пересечения вертикальных (А) и горизонтальных (Б) линий определяют номера задач контрольной работы, записанные столбиком. Например, если личный шифр обучающегося имеет две последние цифры 75, то он должен выполнить номера 3, 13, 23, 40, 49.
Таблица выбора вариантов
| Б А | ||||||||||
Методические указания по выполнению заданий контрольной работы
1. Модель межотраслевого баланса
Задача 1.
В таблице приведены данные об исполнении баланса. Используя модель Леонтьева многоотраслевой экономики, вычислить необходимый объем валового выпуска каждой отрасли, если конечный выпуск энергетической отрасли увеличится вдвое, а машиностроительной сохранится на прежнем уровне.
| № | Отрасль | Потребление | Конечный продукт | Валовой продукт | |
| Энергетическая | |||||
| Машиностроение |
Решение
1) Вычисляем коэффициенты прямых затрат aij, показывающие, какой объем продукции i -ой отрасли идет на производство одной единицы продукции j -ой отрасли:

2) Выписываем столбец валового выпуска X, столбец нового конечного выпуска Y, а также матрицу прямых затрат А.

3) Вычисляем матрицу E-A
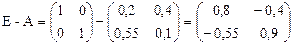
4) Вычисляем матрицу полных затрат S=(E-A)-1. Каждый элемент sij этой матрицы показывает величину валового выпуска i -ой отрасли, необходимого для обеспечения выпуска одной единицы конечного продукта j -ой отрасли.
4.1. Вычисляем определитель 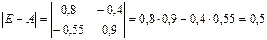
4.2. Находим транспонированную матрицу 
4.3. Строим присоединенную матрицу:


4.4. Находим обратную матрицу: 
5) Вычисляем новый вектор валового выпуска:

6) Строим новую балансовую таблицу, предварительно вычисляя недостающие величины:

| № | Отрасль | Потребление | Конечный продукт | Валовой продукт | |
| Энергетическая | 186,4 | 265,6 | |||
| Машиностроение | 512,6 | 66,4 |
Проверка: 
Графический метод решения задач линейного программирования
Графический метод используется для решения задач с двумя переменными следующего вида:
F(X) = c  x
x  +c
+c  x
x 
 max(min), (1)
max(min), (1)
a  x
x  +a
+a  x
x 
 b
b  ,
,
a  x
x  +a
+a  x
x 
 b
b  , (2)
, (2)
…………………………
a  x
x  +a
+a  x
x 
 b
b 
x 
 0, x
0, x 
 0. (3)
0. (3)
Данный метод основывается на возможности графического изображения области допустимых решений и нахождения среди них оптимального решения.
Областью решений линейного неравенства  является одна из двух полуплоскостей, на которые прямая
является одна из двух полуплоскостей, на которые прямая  соответствующая данному неравенству, делит всю координатную плоскость.
соответствующая данному неравенству, делит всю координатную плоскость.
Для того чтобы определить, какая из двух координатных полуплоскостей является областью решений, достаточно координаты какой-либо точки, не лежащей на прямой, подставить в неравенство: если оно удовлетворяется, то областью решений является полуплоскость, содержащая данную точку, если же неравенство не удовлетворяется, то областью решений является полуплоскость, не содержащая данную точку.
Областью допустимых решений задачи является общая часть  полуплоскостей – областей решений всех неравенств системы ограничений.
полуплоскостей – областей решений всех неравенств системы ограничений.
Для нахождения среди допустимых решений оптимального решения используют линии уровня и опорные прямые.
Линией уровня называется прямая, на которой целевая функция задачи принимает постоянное значение. Уравнение линии уровня в  общем случае имеет вид c
общем случае имеет вид c  x
x  +c
+c  x
x  = l, где l = const. Все линии уровня параллельны между собой. Их нормаль
= l, где l = const. Все линии уровня параллельны между собой. Их нормаль 
Опорной прямой называется линия уровня, которая имеет хотя бы одну общую точку с областью допустимых решений и по отношению, к которой эта область находится в одной из полуплоскостей.
Область допустимых решений любой задачи имеет не более двух опорных прямых, на одной из которых может находиться оптимальное решение.
Значения целевой функции на линиях уровня возрастают, если линии уровня перемещать в направлении их нормали, и убывают при перемещении линий уровня в противоположном направлении.
Задача 2.
Решить задачу линейного программирования
F (X) = 3x  + 2x
+ 2x 
 max,
max,



x 

.
Решение.
Строим область допустимых решений задачи. Нумеруем ограничения задачи. В прямоугольной декартовой системе координат (рис.1) строим многоугольник решений. Для этого в неравенствах системы ограничений и условиях неотрицательности переменных знаки неравенств заменим на знаки точных равенств.
 (4)
(4)
Построив полученные прямые, найдём соответствующие полуплоскости допустимых значений переменных и их пересечение (рис.1). Многоугольником допустимых решений задачи является пятиугольник ABCDE,координаты точек которого удовлетворяют условию неотрицательности переменных и неравенствам системы ограничений задачи.
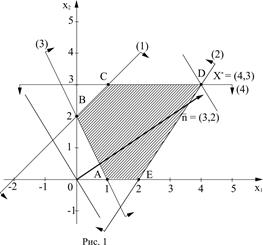
Строим нормаль линии уровня  =(3,2) и одну из этих линий, например, 3x
=(3,2) и одну из этих линий, например, 3x  + 2x
+ 2x  = 0. Так как решается задача на отыскание максимума целевой функции, то линию уровня перемещаем в направлении нормали до опорной прямой. Эта прямая проходит через точку X
= 0. Так как решается задача на отыскание максимума целевой функции, то линию уровня перемещаем в направлении нормали до опорной прямой. Эта прямая проходит через точку X  пересечения прямых, ограничивающих область допустимых решений и соответствующих неравенствам (2) и (4). Определяем координаты точки X
пересечения прямых, ограничивающих область допустимых решений и соответствующих неравенствам (2) и (4). Определяем координаты точки X  . Для этого решим систему уравнений
. Для этого решим систему уравнений


В результате получим X  = (4, 3). Вычисляем
= (4, 3). Вычисляем
F(X  ) =
) = 
Ответ: max F(X) = 18 при X  = (4, 3).
= (4, 3).
Транспортная задача
Одной из типичных задач линейного программирования является так называемая транспортная задача. Она возникает при планировании наиболее рациональных перевозок грузов, а также при организации и планировании производства.
Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из m пунктов отправления А  , А
, А  ,…, А
,…, А  в n пунктов назначения B
в n пунктов назначения B  , B
, B  ,…, B
,…, B  . Заданы стоимости перевозки единицы груза c
. Заданы стоимости перевозки единицы груза c  от каждого i-того пункта отправления до каждого j-того пункта потребления. Требуется определить, какое количество груза x
от каждого i-того пункта отправления до каждого j-того пункта потребления. Требуется определить, какое количество груза x  необходимо перевезти из каждого i-того пункта отправления до каждого j-того пункта потребления так, чтобы:
необходимо перевезти из каждого i-того пункта отправления до каждого j-того пункта потребления так, чтобы:
1. вывезти груз всех поставщиков;
2. удовлетворить спрос всех потребителей;
3. обеспечить минимальные суммарные транспортные расходы на перевозку всех грузов.
При постановке задач перевозки грузов могут возникнуть две различные ситуации:
- количество груза у всех поставщиков равно потребностям всех потребителей в данном грузе;
- количество груза у всех поставщиков больше или меньше потребностей всех потребителей в данном грузе.
В первом случае экономико-математическая модель транспортной задачи называется закрытой, а сама задача – сбалансированной. Во втором случае модель называется открытой, а задача - не сбалансированной.
Математическая модель закрытой транспортной задачи записывается в виде:
F = 




 (10)
(10)

x 
Разрешимой является только закрытая модель или сбалансированная транспортная задача. Чтобы решить несбалансированную транспортную задачу необходимо её сбалансировать, т. е. свести к закрытой модели. В случае, когда запасы в пунктах отправления превосходят потребности всех пунктов назначения, необходимо ввести фиктивного потребителя с потребностью в грузе равной разности общих запасов и общих потребностей. Так как введённый потребитель фиктивный, то все истинные тарифы доставки груза полагают равными нулю.
В случае, когда запасы в пунктах отправления меньше потребностей всех пунктов назначения, необходимо ввести фиктивного поставщика с наличием груза в количестве, равном разности общих потребностей и общих запасов. Так как введённый поставщик фиктивный, то истинные тарифы доставки груза из этого пункта полагают равными нулю.
Чтобы лучше представить условие транспортной задачи, все исходные данные сводят в таблицу, называемую матрицей планирования перевозок. Строки таблицы соответствуют поставщикам, а столбцы потребителям. В последней строке записывают заявки каждого потребителя, а в последнем столбце запасы каждого поставщика. В верхних правых углах внутренних клеток таблицы записываются истинные тарифы c  , а в нижних левых углах – планируемые перевозки x
, а в нижних левых углах – планируемые перевозки x  .
.
Транспортная задача является задачей линейного программирования, поэтому она может быть решена симплексным методом. Следует отметить особенности экономико-математической модели транспортной задачи по сравнению с другими моделями задач линейного программирования:
- система ограничений есть система уравнений, т.е. транспортная задача задана в канонической форме;
- коэффициенты при переменных системы ограничений равны единице или нулю.
Специфичность формы системы ограничений данной задачи позволяет существенно упростить обычный симплексный метод. Модификация симплексного метода применительно к транспортной задаче называется распределительным методом. По аналогии с обычным случаем решение в нём осуществляется по шагам. При этом каждому шагу соответствует разбиение переменных на основные (базисные) и неосновные (свободные). Число базисных переменных закрытой транспортной задачи равно m+n-1, где m - число поставщиков, n - число потребителей. Каждому разбиению переменных x 
 задачи на базисные и свободные соответствует базисное решение и, как следствие, заполнение таблицы поставок, которое называется базисным. При этом заполненным клеткам соответствуют базисные переменные, а свободным – свободные.
задачи на базисные и свободные соответствует базисное решение и, как следствие, заполнение таблицы поставок, которое называется базисным. При этом заполненным клеткам соответствуют базисные переменные, а свободным – свободные.
Подобно тому, как это было в симплексном методе, в распределительном методе решения транспортной задачи необходимо переходить от одного базисного распределения поставок к другому в сторону не возрастания целевой функции вплоть до оптимального решения. Для начала такого движения необходимо найти исходное базисное распределение поставок – так называемый опорный план.
Существуют три метода отыскания исходного опорного плана транспортной задачи: метод «северо-западного угла», метод минимальной стоимости и метод Фогеля. Построенный одним из методов исходный опорный план доводят до оптимального путем последовательного улучшения с помощью метода потенциалов.
Решение транспортной задачи рассмотрим на конкретном примере.
Задача 3.
На трех складах оптовой базы имеется однородный груз в количествах 40, 80 и 80 единиц. Этот груз необходимо перевезти в четыре магазина, каждый из которых должен получить соответственно 70,20, 60 и 60 единиц. Стоимости доставки единицы груза (тарифы) из каждого склада A  (i =1, 2, 3) во все магазины B
(i =1, 2, 3) во все магазины B  (j = 1, 2, 3, 4) заданы матрицей C=(
(j = 1, 2, 3, 4) заданы матрицей C=( )
)
С = 
Составить план перевозок однородного груза с минимальными транспортными затратами.
Решение.
1. Проверяем необходимое и достаточное условие разрешимости задачи:
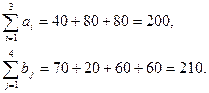
Как видно, суммарная потребность в грузе превышает его запасы на складах оптовой базы. Следовательно, модель транспортной задачи является открытой и в исходном виде решения не имеет. Для получения закрытой модели введём дополнительный (фиктивный) склад A  c запасом груза, равным a
c запасом груза, равным a  =210-200=10. Тарифы перевозки единицы груза из склада A
=210-200=10. Тарифы перевозки единицы груза из склада A  во все магазины полагаем равными нулю. Все исходные данные заносим в таблицу 3.1.
во все магазины полагаем равными нулю. Все исходные данные заносим в таблицу 3.1.
Таблица 3.1
| Поставщики | Потребители | Запасы | |||
B 
| B 
| B 
| B 
| a 
| |
A 
| |||||
A 
| |||||
A 
| |||||
A 
| |||||
Потребности
b 
| 210= 210 |
2. Построение первого опорного плана методом минимальной стоимости.
Среди тарифов минимальным является c  =1. В клетку А
=1. В клетку А  В
В  направляем максимально возможный груз, равный min(60,40)=40. Тогда x
направляем максимально возможный груз, равный min(60,40)=40. Тогда x  = 40. Из склада А
= 40. Из склада А  весь груз вывезен, но потребность четвертого магазина неудовлетворенна на 20 ед. Строка А
весь груз вывезен, но потребность четвертого магазина неудовлетворенна на 20 ед. Строка А  выходит из рассмотрения.
выходит из рассмотрения.
Среди оставшихся тарифов минимальный элемент - c  = 2. В клетку A
= 2. В клетку A  B
B  направляем груз min (60,80) =60. При этом столбец B
направляем груз min (60,80) =60. При этом столбец B  выходит из рассмотрения, а из склада A
выходит из рассмотрения, а из склада A  не вывезено 20 ед.
не вывезено 20 ед.
Продолжая рассуждения аналогичным образом, получаем первый опорный план, который является допустимым, так как все грузы со складов вывезены, и потребности всех магазинов удовлетворены.
3. Проверка вырожденности плана.
Число базисных переменных в невырожденном плане должно быть m+n-1 = 4+4-1 = 7. Первый опорный план является вырожденным, так как число занятых клеток равно шести. Для продолжения решения задачи опорный план необходимо дополнить введением фиктивной перевозки, т. е. занять нулём одну из свободных клеток. Направляем нуль в клетку A  B
B  , так как данная клетка не образует с другими занятыми клетками таблицы замкнутого прямоугольного контура.
, так как данная клетка не образует с другими занятыми клетками таблицы замкнутого прямоугольного контура.
4. Расчет значения целевой функции.
F(X  ) =
) =  =
=
560 (тыс. руб.).
5. Нахождение оптимального плана транспортной задачи.
Построенный исходный опорный план доводим до оптимального методом потенциалов. Основой вычислительного процесса при улучшении опорного плана является определение критерия оптимальности  :
: 
 = с
= с  ,
,
где c  - затраты (истинные тарифы), связанные с доставкой одной единицы груза из i-того пункта отправления в j-ый пункт назначения;
- затраты (истинные тарифы), связанные с доставкой одной единицы груза из i-того пункта отправления в j-ый пункт назначения;
c  - расчётные затраты (косвенные тарифы), связанные с доставкой одной единицы груза из i-того пункта отправления в j-ый пункт назначения, определяемые для тех клеток опорного плана, ресурсы в которые не распределены (для незаполненных клеток).
- расчётные затраты (косвенные тарифы), связанные с доставкой одной единицы груза из i-того пункта отправления в j-ый пункт назначения, определяемые для тех клеток опорного плана, ресурсы в которые не распределены (для незаполненных клеток).
План транспортной задачи является оптимальным, если для всех свободных клеток таблицы перевозок значение критерия оптимальности 
 . Если для всех свободных клеток таблицы перевозок критерий оптимальности
. Если для всех свободных клеток таблицы перевозок критерий оптимальности  <0, то этот план перевозок является единственным. Если для некоторых свободных клеток таблицы перевозок критерий оптимальности
<0, то этот план перевозок является единственным. Если для некоторых свободных клеток таблицы перевозок критерий оптимальности 
 =0, то этот оптимальный план перевозок не является единственным. Наконец, если имеются свободные клетки, для которых критерий оптимальности
=0, то этот оптимальный план перевозок не является единственным. Наконец, если имеются свободные клетки, для которых критерий оптимальности  >0, то полученный план перевозок не является оптимальным.
>0, то полученный план перевозок не является оптимальным.
Алгоритм метода потенциалов состоит в следующем: каждому поставщику A  ставится в соответствие некоторое число u
ставится в соответствие некоторое число u  , которое называется потенциалом A
, которое называется потенциалом A  -того поставщика; каждому потребителю B
-того поставщика; каждому потребителю B  ставится в соответствие некоторое число v
ставится в соответствие некоторое число v  , которое называется потенциалом B
, которое называется потенциалом B  -того потребителя. Для каждой заполненной клетки, т. е. для каждой базисной переменной строится соотношение:
-того потребителя. Для каждой заполненной клетки, т. е. для каждой базисной переменной строится соотношение:
u  +v
+v  =c
=c 
Получаем систему с числом уравнений, равным количеству базисных переменных. Из этой системы определяем неизвестные потенциалы u  и v
и v  , полагая u
, полагая u  =0. Для каждой незаполненной клетки, т. е. для каждой небазисной переменной, рассчитываются косвенные тарифы c
=0. Для каждой незаполненной клетки, т. е. для каждой небазисной переменной, рассчитываются косвенные тарифы c  по формуле: c
по формуле: c  = u
= u  +v
+v  . Затем полученный план проверяют на оптимальность по критерию оптимальности
. Затем полученный план проверяют на оптимальность по критерию оптимальности  . Если для каждой незаполненной клетки выполняется условие:
. Если для каждой незаполненной клетки выполняется условие:  , то исходный план является оптимальным. Если некоторые
, то исходный план является оптимальным. Если некоторые  >0, то необходимо перейти к новому плану путем перемещения перевозки в клетку, отвечающую условию max
>0, то необходимо перейти к новому плану путем перемещения перевозки в клетку, отвечающую условию max  . Если таких клеток несколько, то выбирают любую из них.
. Если таких клеток несколько, то выбирают любую из них.
Для правильного перемещения перевозок, чтобы не нарушить ограничения задачи, строят так называемый цикл, т. е. замкнутый многоугольник, соединяющий выбранную клетку с ней же самой и проходящий через заполненные клетки.
Цикл строится следующим образом: вычёркиваются (мысленно) все строки и столбцы, содержащие ровно одну заполненную клетку, при этом считается, что выбранная клетка без поставки является заполненной; все оставшиеся после вычеркивания клетки составляют цикл и лежат в его углах, они соединяются ломаной линией.
В каждую клетку цикла, начиная с незаполненной, поочередно вписывают знаки “+” и “-“. В клетках с отрицательными знаками выбирается минимальная величина поставки, обозначаемая как  . В те вершины, которые имеют знак “+” прибавляется поставка
. В те вершины, которые имеют знак “+” прибавляется поставка  , а в вершинах со знаком “-“ поставки уменьшаются на величину
, а в вершинах со знаком “-“ поставки уменьшаются на величину  . При этом суммы поставок по строкам и столбцам не изменяются. В результате клетка, для которой строился цикл, станет занятой, а в одной из бывших занятых клеток окажется нулевая поставка и её надо объявить свободной. Общее количество заполненных клеток не изменится, следовательно, новый план перевозок является невырожденным.
. При этом суммы поставок по строкам и столбцам не изменяются. В результате клетка, для которой строился цикл, станет занятой, а в одной из бывших занятых клеток окажется нулевая поставка и её надо объявить свободной. Общее количество заполненных клеток не изменится, следовательно, новый план перевозок является невырожденным.
Если в результате пересчета одновременно в нескольких ранее занятых клетках цикла поставки примут нулевые значения, то свободной объявляется лишь одна из них. Остальные считаются условно занятыми с нулевыми поставками.
Значения переменных, включенных в цикл, после пересчета переносятся в новую таблицу без изменений. Полученный новый план проверяется на оптимальность.
Такое улучшение плана можно проводить неоднократно до тех пор пока все критерии для незаполненных клеток окажутся 
 0. Затем вычисляется оптимальная стоимость перевозок.
0. Затем вычисляется оптимальная стоимость перевозок.
Вернёмся к нашему примеру. Найдём потенциалы u  и v
и v  по занятым клеткам из соотношений:
по занятым клеткам из соотношений:
u  +v
+v  =c
=c  =1, u
=1, u  +v
+v  =c
=c  =3,
=3,
u  +v
+v  =c
=c  =2, u
=2, u  +v
+v  =c
=c  = 3,
= 3,
u  +v
+v  =c
=c  =4, u
=4, u  +v
+v  =c
=c  = 6,
= 6,
u  +v
+v  =c
=c  =0.
=0.
Получили семь уравнений с семью неизвестными. Полагая u  =0, находим остальные неизвестные.
=0, находим остальные неизвестные.
u  =0, u
=0, u  =2, u
=2, u  =5, u
=5, u  =-1; v
=-1; v  =-1, v
=-1, v  =1, v
=1, v  =0, v
=0, v  =1.
=1.
Заносим значения потенциалов в таблицу 3.2.
Находим косвенные тарифы для незаполненных клеток и проверяем условия оптимальности:
c  = u
= u  +v
+v  = -1<c
= -1<c  =5,
=5,  =-6, c
=-6, c  = u
= u  +v
+v  =1<c
=1<c  =4,
=4,  =-3,
=-3,
с  = u
= u  +v
+v  =0 <c
=0 <c  =2,
=2,  =-2, с
=-2, с  = u
= u  +v
+v  =1<c
=1<c  =4,
=4,  =-3,
=-3,
с  =u
=u  +v
+v  =6>c
=6>c  =3,
=3,  =3>0, с
=3>0, с  =u
=u  +v
+v  =5>c
=5>c  =3,
=3, 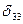 =2>0
=2>0
c  =u
=u  +v
+v  =-2<c
=-2<c  =0,
=0,  =-2, c
=-2, c  =u
=u  +v
+v  =0=c
=0=c  =0,
=0,  =0,
=0,
c  = u
= u  +v
+v  =-1<c
=-1<c  =0,
=0,  =-1.
=-1.
Первый опорный план является не оптимальным, так как  =3 >0 и
=3 >0 и 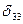 =2 >0. Выбираем максимальное значение
=2 >0. Выбираем максимальное значение  . Для улучшения плана клетку A
. Для улучшения плана клетку A  B
B  необходимо загрузить, т.е. переменную x
необходимо загрузить, т.е. переменную x  ввести в состав базисных и построить для неё цикл пересчета поставок.
ввести в состав базисных и построить для неё цикл пересчета поставок.
Таблица 3.2
| Поставщики | Потребители | Запасы | ||||
B 
| B 
| B 
| B 
| |||
u  /v /v 
| -1 | 1 | 0 | 1 | ||
A 
| 0 | |||||
A 
| 2 |  - 3 - 3
| + 3 | |||
A 
| 5 |  3 3
| - 6 | |||
A 
| -1 | |||||
| Потребности | 210= 210 |
Мысленно вычеркнем в таблице 3.2 первый, и третий столбцы, а также первую и четвертую строки, так как они содержат по одной заполненной клетке. Оставшиеся четыре заполненные клетки, включая введенную нами, образуют цикл. В клетках цикла, начиная с клетки (3,2), проставим поочередно знаки “+” и “-“. В клетках с отрицательными знаками выберем наименьшее значение из поставок
Поделиться:
Поиск по сайту
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2017-06-12
Нарушение авторских прав и Нарушение персональных данных