БМФ будут в билете ниже.

+ Основные теоремы о пределах.

1. Предел константы равен этой же константе;

2. Константный множитель можно вынести за предел;

3. Предел суммы функций равен сумме пределов функций;

4. Предел произведения функций равен произведению пределов функций;

5. Предел частного функций равен частному пределов функций;

6. Предел показательно-степенной функции равен пределу показателя в степени, равной пределу степени исходной функции.

 

++Виды неопределённостей. Вычисление неопределённостей.

++Первый замечательный предел. Второй замечательный предел.

+ Бесконечно малые функции. Бесконечно большие функции.

α(x) – бесконечно малая при x → x₀, если предел равен 0.

Аналогично U(x) – бесконечно большая при x → x₀, если предел равен бесконечности.

+ Выделение главной части бесконечно малых и бесконечно больших функций.

Если α(x) и β(x) бесконечно малые при x → x₀ и β(x) эквивалентна C(α(x))^k, где C!= 0 и k – константы, то C(α(x))^k – главная часть β(x), k – порядок β(x) относительно α(x).

· x₀ – константа, β(x) эквивалентна C(x – x₀)^k

· x₀ – бесконечность, β(x) эквивалентна C(1/x)^k

Если U(x) и ψ(x) бесконечно большие при x → x₀, а ψ(x) эквивалентна C(U(x))^k, где C!= 0 и k – константы, то C(U(x))^k – главная часть ψ(x), k – порядок ψ(x) относительно U(x).

· x₀ – константа, ψ(x) эквивалентна C(1 / (x – x₀))^k

· x₀ – бесконечность, ψ(x) эквивалентна C(x)^k

Для выделения главной части бесконечно малых и бесконечно больших функций используют следующие теоремы:

1. Если предел функции f(x) равен С – константе, C принадлежит интервалу (0, inf), то f(x)α(x) эквивалентна Cα(x) при x → x₀

2. Если α(x) эквивалентна α₁(x) и β(x) эквивалентна β₁(x) при x → x₀, то:

a. α(x)β(x) эквивалентна α₁(x)β₁(x)

b. α(x) / β(x) эквивалентна α₁(x) / β₁(x)

3. Если α(x) эквивалентна β(x) и β(x) эквивалентна γ(x) при x → x₀, то α(x) эквивалентна γ(x)

4. Сумма бесконечно малых функций разного порядка эквивалентна бесконечно малой функции меньшего порядка

5. Сумма бесконечно больших функций разного порядка эквивалентна бесконечно большой функции большего порядка

+ Сравнение бесконечно малых функций. Эквивалентные бесконечно малые.

Если нужно сравнить бесконечно малые и бесконечно большие функции, то нужно сравнить порядок этих функций.

+ Определение непрерывности функции одной переменной.

f(x) непрерывна в точке x₀, если:

1. f(x) определена в точке x₀;

2. Существуют конечные односторонние пределы в этой точке;

3. Эти пределы равны значению функции в точке x₀.

+ Точки разрыва первого рода функции одной переменной.

Если односторонние пределы в точке не равны, то эта точка – точка разрыва 1-го рода, а величина δ, разница между пределами, называется скачком функции.

Если односторонние пределы в точке равны между собой, но не равны значению функции в точке, то эта точка – точка устранимого разрыва 1-го рода. Чтобы устранить разрыв, нужно переопределить или доопределить функцию в точке разрыва, т.е. ввести новую функцию.

+ Точки разрыва второго рода функции одной переменной.

Если односторонние пределы в точке не определены или равны бесконечности, то эта точка – точка разрыва второго рода.

+ Определение производной. Её физический смысл. Геометрический смысл производной.

Пусть:

· f(x) задана на (a; b) и x₀ принадлежит (a; b)

· Δx – приращение аргумента в x₀, Δ(x) принадлежит (a; b)

· Δy = f(x₀ + Δx) – f(x₀) – приращение функции

Тогда f’(x₀) = lim Δx → 0 (Δy / Δx)

Физический смысл производной: производная от расстояния по времени есть скорость.

Геометрический смысл производной: производная равна тангенсу угла между OX и касательной к функции в точке x₀.

+ Дифференцируемая функция.

Если f(x), заданная на (a; b), имеет конечную производную в точке x₀, принадлежащей (a; b), то она дифференцируема в этой точке.

+ Правила дифференцирования.

1. f(x) = const → f’(x) = 0

2. (f(x) ± g(x))’ = f’(x) ± g’(x)

3. (f(x) * g(x))’ = f’(x) * g(x) + f(x) * g’(x)

4. (cf(x))’ = cf’(x)

5. (f(x) / g(x))’ = (f’(x) * g(x) – f(x) * g’(x)) / g²(x)

++Производные основных элементарных функций.

± Дифференциал. Его свойства.

Дифференциал – это приращение графика касательной (понятность определения зашкаливает).

dy = f’(x) * dx

Свойства дифференциала (u и v – функции от x, c – константа):

1. d(u ± v) = du ± dv

2. d(uv) = udv + vdu

3. d(cu) = cdu

4. d(u/v) = (vdu - udv) / v²

++Производная сложной функции.

++Производная функций, заданных параметрически.

+ Дифференцирование функций, заданных неявно.

Пусть дан функционал F(x, y) = 0. Если y = f(x), то функция задана явно, и всё хорошо, в противном случае возьмём F’(x, y) и выразим y’ через всё остальное.

+ Уравнение касательной к кривой. Угол между кривыми.

Если f(x) дифференцируема в точке x₀, то уравнение касательной в этой точке:

y = f’(x₀) * (x – x₀) + f(x₀)

Углом между кривыми на плоскости в их общей точке называется наименьший из двух возможных углов между касательными к этим кривым в данной точке. Если уравнения касательных, проведенных к кривым и , соответственно и , то тангенс угла между кривыми определяется соотношением:

± Вычисление дифференциала. Приближённое вычисление с помощью дифференциала.

Приращение 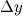функции представимо в виде:

где функция является б.м. функцией при стремлении аргумента к нулю. Так как , то

В силу того, что второе слагаемое является бесконечно малым, то им можно пренебречь, а поэтому

А так как в нахождении дифференциал значительно проще, чем приращение функции, то данная формула активно используется на практике.

Для приближенного вычисления значения функции применяется следующая формула:

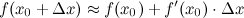
++Логарифмическое дифференцирование.

+ Производные высших порядков.

Пусть f(x) дифференцируема на (a; b). Тогда:

f⁽ⁿ⁾(x) = (f^(n-1)(x))’, n – порядок производной.

+ Дифференциалы высших порядков.

Если существует дифференциал n-1-го порядка f(x), то дифференциал n-го порядка:

dⁿf(x, dx) = f⁽ⁿ⁾(x)(dx)ⁿ

+ Основные теоремы дифференциального исчисления. Теорема Ферма. Теорема Ролля.

Теорема Ферма: Пусть f(x) имеет на интервале D точку экстремума x₀, причём D содержит некую окрестность x₀ (т.е. D = (x₀ – δ; x₀ + δ)). Тогда f’(x₀) = 0 либо f’(x₀) не существует.

Теорема Ролля: Пусть f(x) дифференцируема на интервале (a; b) и непрерывна в конечных точках a и b. f(a) = f(b) = 0. Тогда найдётся хотя бы одна точка x0 ∈ (a; b), где f’(x₀) = 0.
Другими словами, между двумя корнями a и b дифференцируемой функции f(x) обязательно найдётся корень x₀ её производной.

+ Основные теоремы дифференциального исчисления. Теорема Лагранжа. Теорема Коши.

Теорема Лагранжа: Пусть f(x) дифференцируема на интервале (a; b) и непрерывна в конечных точках a и b. Тогда на (a; b) найдётся точка x0 такая, что:

f’(x0) = (f(b) – f(a)) / (b - a) ↔ f(b) – f(a) = f’(x₀) * (b - a) ↔ Δf = f’(x₀) * Δx

Теорема Коши: Пусть x = φ(t), y = ψ(t), t∈ [α; β] – функция, заданная параметрически и дифференцируемая на на (α; β), причём φ’(x)!= 0 на t ∈ (α; β). Тогда найдётся t₀∈ (α; β) такая, что:

(ψ(β) – ψ(α)) / (φ(β) – φ(α)) = ψ’(t) / φ’(t) – производная параметрически заданной функции.

++Правило Лопиталя, его приложение для раскрытия неопределённостей различного вида.

+ Монотонность функции. Признаки монотонности.

f(x) называется возрастающей (убывающей) на [a; b], если для ∀ x₁, x₂∈ [a; b], удовлетворяющих условию x₁>x₂, справедливо f(x₁) >f(x₂) (f(x₁) <f(x₂)).

Признак монотонности: Пусть f(x) дифференцируема на [a; b]. Тогда если f’(x) > 0 (f’(x) < 0) для ∀x ∈ [a; b], то f(x) возрастает (убывает) на [a; b].

++Исследование функций с помощью первой производной.

++Исследование функций с помощью второй производной.

+ Исследование функции без привлечения производных. Вертикальные, горизонтальные и наклонные асимптоты.

· Вертикальные асимптоты: x = a, limx → a (f(x)) = inf

· Горизонтальные асимптоты: y = b, limx → inf (f(x)) = const

· Наклонные асимптоты: y = kx + b, k = limx → inf (f(x) / x), b = lim x → inf (f(x) - kx)

+ Схема построения графиков функций.

1. Найти ООФ

2. Чётность и периодичность

3. Корни и знаки функции

4. Исследование с помощью первой производной: монотонность, экстремумы

5. Исследование с помощью второй производной: выпуклость, перегибы

6. Асимптоты

7. График