Случайное событие, которое невозможно представить как объединение или пересечение более простых событий, называется элементарным событием. Вероятность наступления события p(A) определяется как отношение числа m элементарных событий, благоприятствующих наступлению события, к общему числу n элементарных событий. Эта формула носит название классической вероятности:
(2.1)
Событие, противоположное событию А ( не -A), обозначается как 
. Вероятности исходного и противоположного события связаны формулой:
(2.2)
Произведением событий AB называется новое событие, состоящее в одновременном появлении событий A и B. Суммой событий A+B называется новое событие, состоящее в появлении либо события A, либо события B, либо обоих этих событий. События называются несовместными, если они не могут произойти одновременно. События образуют полную группу, если они попарно несовместны, а сумма их вероятностей равна 1. Вероятность суммы событий вычисляется так:
p (A+B) = p (A) + p (B) – p (AB) (2.3)
В случае несовместности событий последнее слагаемое обращается в ноль. События называются независимыми, если вероятность появления одного из них не зависит от появления другого. Вероятность произведения независимых событий равна:
p (AB) = p (A) p (B) (2.4)
Условная вероятность 
означает вероятность события A при условии, что событие B произошло. В случае зависимых событий вероятность произведения равна:
p (AB) = p (A) p (B/A) (2.5)
Предположим, что событию A предшествуют n взаимно исключающих друг друга гипотез Hi. Вероятности этих гипотез должны удовлетворять равенству 
. Тогда полная вероятность события A определяется так:
(2.6)
Пусть проводится конечное число n последовательных независимых испытаний, в каждом из которых некоторое событие A может наступить с одинаковой вероятностью p.
Вероятность того, что в серии из n независимых испытаний событие A наступит k раз, равно (формула Бернулли):
(2.7)
Важной количественной мерой информации является неопределённость. Чем больше исходов опыта, тем выше его неопределённость. В случае одного исхода опыта неопределённость равна 0. Мера неопределённости называется энтропией. Энтропия H опыта связана с числом его исходов S:
H = log2 S (2.8)
Поскольку знание исхода опыта A полностью снимает его неопределённость, полученная в опыте A информация численно равна энтропии:
H (A) = I (A) (2.9)
Первая буква синтаксической информации обладает, очевидно, наибольшей неопределённостью, поэтому информация первой буквы – максимальна. Согласно простейшей модели угадывания, информация непрерывно убывает, обращаясь в 0 для последней буквы, которой считается пробел. Это объясняется тем фактом, что чем больше букв слова мы уже знаем, тем легче нам вычислить вероятность появления оставшихся букв.
Пример 1. Студент при построении фразы может ошибиться в морфологии с вероятностью 0,6, а в синтаксисе – 0,3. Найти вероятность того, что при переводе фразы студент
a) ошибётся в морфологии или в синтаксисе
b) ошибётся или в морфологии, или в синтаксисе.
c) ошибётся в морфологии и в синтаксисе
d) ошибётся в морфологии, но не в синтаксисе.
Введём элементарные события: A – “студент ошибётся в морфологии”, B – “студент ошибётся в синтаксисе”.
a) Поскольку происходит одно из событий, воспользуемся формулой сложения вероятностей (2.3), отметив, что события совместны – значит, последнее слагаемое не обращается в ноль:
p = 0,6 + 0,3 – 0,18 = 0,72.
b) Здесь используется та же формула (2.3), но события уже не являются совместными (“или” …, “или” …), и последнее слагаемое исчезает:
p = 0,6 + 0,3 = 0,9.
c) Здесь происходят оба события, поэтому применяется формула умножения вероятностей (2.4):
p = 0,6 · 0,3 = 0,18.
d) Вероятность того, что студент не ошибётся в синтаксисе, вычисляется по формуле (2.2), а затем для общей вероятности применяется формула (2.4):
p = 0,6 · (1 – 0,3) = 0,42.
Пример 2. Дешифровщик обозначил графемы неизвестного слова как ABCDA. Вероятность правильности чтения каждой графемы он оценивает как 0,4. Найти вероятность того, что хотя бы одна из графем прочтена им верно.
Пусть событие A – “одна из графем прочтена верно”. Перейдём к противоположному событию – “ни одна из графем не прочтена верно”. Это – вероятность произведений противоположных событий. По формуле (2.4)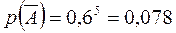 
. Тогда по формуле (2.2) получаем: 
.
Пример 3. Впростом слове, не содержащем инфиксов или трансфиксов, 8 букв. Найти вероятность того, что длина корня – три буквы.
Поскольку в слове отсутствуют инфиксы или трансфиксы, буквы корня идут подряд. Значит, они могут занимать позиции в слове 123, 234…678. Таких вариантов 6. Теперь вычислим комбинации, при которых число букв корня меняется от 1 до 8. Если в корне 1 буква, то у неё 8 вариантов расположения: 1, 2, 3…8. Если в корне 2 буквы, то 7 вариантов: 12, 23, 34…78. Таким образом, найдём искомую вероятность по формуле (2.1): 
.
Пример 4. Во фразе 8 знаменательных слов: 2 глагола, 3 существительных и 3 прилагательных. Этимология глаголов филологу известна точно, этимология существительных с вероятностью 0,8, а этимология прилагательных – с вероятностью 0,7. Найти вероятность того, что филолог правильно определит этимологию любого слова из фразы.
Введём гипотезы: H1 – “слово является глаголом”, H2 – “слово является существительным”, H3 – “слово является прилагательным”. Вычислим их вероятности: p(H1) = 2/8 = 1/4, p(H2) = p(H3) = 3/8. Событие A – “филолог правильно определит этимологию слова”. Условные вероятности: p(A/H1) = 1, p(A/H2) = 0,8, p(A/H3) = 0,7. Тогда по формуле (2.6) получается:
p(A) = p(A/H1) p(H1) + p(A/H2) p(H2) + p(A/H3) p(H3) = 1/4 + 3/8 * (0,8 + 0,7) = 0, 8125.
Пример 5. Информант, носитель одного из диалектов, правильно переводит фразу на литературный язык с вероятностью 0,7. Найти вероятность того, что двое из пяти информантов правильно переведут фразу на литературный язык.
Применяем формулу Бернулли (p = 0,7, k=2, n=5).
Пример 6. Имеется трёхсловное предложение, каждое из слов которого выбирается из нескольких вариантов. Например, “ Дима (Никита) любит (уважает) Катю (Надю, Свету, Алину) ”. Найти энтропию фразы.
Энтропия фразы складывается из энтропий её слов. Для первых двух слов существует 2 варианта, а для третьего четыре, поэтому H = H1 + H2 + H3 = log2 2 + log2 2 + log2 4 = log2 16 = 4.
Пример 7. Найти синтаксическую информацию трёх последних значимых букв слова “ филология ”.
Мы уже знаем первые шесть букв слова, и нам нужно угадать три последних буквы (самой последней буквой считается пробел, его мы здесь не учитываем). После “ филоло- “ может стоять только буква г, поэтому I (г) = H (г) = log21 = 0. Для предпоследней буквы имеется 5 вариантов: и, а, у, о, е. Эти варианты мы для простоты считаем равнозначными. Поэтому I (и) = H (и) = log25.
Для последней же буквы – 3 варианта: я, и, ч. I (я) = H (я) = log23.