Проекцией вектора  на ось
на ось  (рис. 1) называется взятая с соответствующим знаком длина отрезка
(рис. 1) называется взятая с соответствующим знаком длина отрезка  , заключенного между проекциями начала и конца вектора
, заключенного между проекциями начала и конца вектора  на эту ось. Проекция берется со знаком "плюс", если перемещение от
на эту ось. Проекция берется со знаком "плюс", если перемещение от  к
к  совпадает с положительным направлением оси
совпадает с положительным направлением оси  , и, если нет, то со знаком "минус»,
, и, если нет, то со знаком "минус»,  или
или  .
.

| Рисунок |
Согласно определению, проекция вектора на ось есть величина скалярная: положительная или отрицательная, в зависимости от того, острый иди тупой угол образует проектируемый вектор с осью проекций.
Из самого определения проекции вектора на ось следует, что проекция не изменится, если мы будем переносить вектор параллельно самому себе или если будем проектировать на различные, но параллельные и одинаково направленные оси.

| Проекцией вектора  на плоскость на плоскость 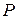 называется вектор называется вектор 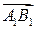 , заключенный между проекциями начала и конца вектора , заключенный между проекциями начала и конца вектора  на эту плоскость (рис. 2). По определению на эту плоскость (рис. 2). По определению  есть вектор, который характеризуется не только своим численным значением, но и направлением в плоскости есть вектор, который характеризуется не только своим численным значением, но и направлением в плоскости 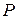 . Модуль вектора . Модуль вектора  определяется равенством определяется равенством  , где , где 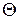 – угол между векторами – угол между векторами  и и  . .
| |
| Рисунок | ||
Суммой двух свободных векторов называется вектор, совпадающий по величине и направлению с диагональю параллелограмма, построенного на этих векторах. Сумма нескольких векторов есть вектор, который изображается замыкающей стороной ломаной линии, составленной из слагаемых векторов. При этом начало каждого последующего вектора откладывается от конца предыдущего, а замыкающий вектор направлен от начала первого слагаемого вектора к концу последнего. Составленный таким способом многоугольник носит название векторного многоугольника, а сам метод – правила векторного многоугольника. Если ломаная линия, составленная из слагаемых векторов, самозамыкается, т. е. если конец последнего из слагаемых векторов совпадает с началом первого, то сумма векторов равна нулю.
В векторном исчислении различают два вида умножения векторов: скалярное и векторное.

| 1. Скалярным произведением двух векторов  и и 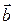 называется скалярная величина, равная произведению модулей называется скалярная величина, равная произведению модулей  и и  этих векторов, умноженному на косинус угла между ними (рис. 3). По определению этих векторов, умноженному на косинус угла между ними (рис. 3). По определению  . .
| |
| Рисунок 3 | ||
Скалярное произведение двух векторов можно рассматривать как произведение модуля одного вектора на проекцию на него другого, т. е.
 .
.
Из этого равенства следует, что:
а) скалярное произведение двух взаимно перпендикулярных векторов равно нулю;
б) скалярный квадрат вектора равен квадрату его модуля, т. е.  . Здесь
. Здесь  .
.
2. Векторное произведение есть вектор (рис. 4), модуль которого равен произведению модулей перемножаемых векторов, умноженному на синус угла между ними.

| Направлен перпендикулярно к плоскости, проходящей через векторы  и и 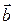 , причем в ту сторону, чтобы, смотря с конца полученного вектора , причем в ту сторону, чтобы, смотря с конца полученного вектора  , видеть кратчайший поворот первого вектора до совмещения со вторым против хода часовой стрелки (рис. 4). По определению вектор векторного произведения определяется по формуле , видеть кратчайший поворот первого вектора до совмещения со вторым против хода часовой стрелки (рис. 4). По определению вектор векторного произведения определяется по формуле
| |
| Рисунок 4 | ||
 , а его модуль
, а его модуль
 .
.
Из последнего равенства следует, что:
1) модуль векторного произведения двух векторов численно равен площади параллелограмма, построенного на этих векторах (рис. 4);
2) векторное умножение двух векторов свойством коммутативности (переместительности) не обладает, так как 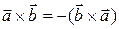 .
.
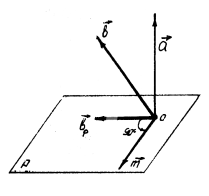
| Геометрически векторное произведение  можно найти следующим построением (рис. 5): проводим плоскость Р, перпендикулярную вектору можно найти следующим построением (рис. 5): проводим плоскость Р, перпендикулярную вектору  , строим ортогональную проекцию вектора , строим ортогональную проекцию вектора 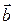 на плоскость Р и поворачиваем эту проекцию в плоскости Р вокруг точки О на 90° против хода часовой стрелки (если смотреть на плоскость с конца вектора на плоскость Р и поворачиваем эту проекцию в плоскости Р вокруг точки О на 90° против хода часовой стрелки (если смотреть на плоскость с конца вектора  ). Полученный вектор ). Полученный вектор  является векторным произведением является векторным произведением 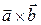 . .
| |
| Рисунок 5 | ||