Статика
Равнодействующая двух пересекающихся сил–  ; диагональ параллелограмма
; диагональ параллелограмма  . Равнодействующая сходящихся сил
. Равнодействующая сходящихся сил  .
.
Проекции силы на оси координат (для плоской системы сил):  .
.
Модуль силы: 
 ; направляющие косинусы:
; направляющие косинусы:  разложение на составляющие:
разложение на составляющие:  .
.
Для пространственной системы:  ,
,  ,
,
 ;
; 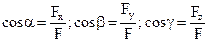 .
.
Проекции равнодействующей системы сходящихся сил на координатные оси: Rx=åFix; Ry=åFiy; Rz=åFiz;  .
.
Условия равновесия сист. сходящихся сил: геометрическое:  , аналитические: åFix=0; åFiy=0; åFiz=0.
, аналитические: åFix=0; åFiy=0; åFiz=0.
Условие равновесия пар сил:  .
.
Момент силы относительно точки: 
 – векторное произведение. Модуль векторного произведения:
– векторное произведение. Модуль векторного произведения:  R×F×sina= F×h. Плоская система сил:
R×F×sina= F×h. Плоская система сил:  , >0 – против час.стр.; <0 – по час.стр.
, >0 – против час.стр.; <0 – по час.стр.
 , проекции момента силы на оси координат:
, проекции момента силы на оси координат:  ,
,  ,
, 
Условия равновесия плоской системы сил: аналитические:  , или
, или  , А,В,С – точки не на одной прямой, или
, А,В,С – точки не на одной прямой, или  , ось "х" не перпендикулярна отрезку АВ.
, ось "х" не перпендикулярна отрезку АВ.
Для пространственной системы сил:
Главный вектор  и главный момент
и главный момент  ,
,
Статические инварианты: 1-ый – квадрат модуля главного вектора: I1= Fo2= Fx2+Fy2+Fz2; 2-ой – скалярное произв. главного вектора на гл. момент: I2=  =Fx×Mx+Fy×My+Fz×Mz.
=Fx×Mx+Fy×My+Fz×Mz.
Момент силы относительно оси: 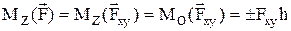 . Моменты силы относительно осей координат: Мx(
. Моменты силы относительно осей координат: Мx( )=yFz – zFy; Мy(
)=yFz – zFy; Мy( )=zFx – xFz; Мz(
)=zFx – xFz; Мz( )=xFy – yFx.
)=xFy – yFx.
Проекция гл. момента на направление гл. вектора  . Мmin=M*
. Мmin=M*
уравнения центральной оси:  .
.
Условия равновесия пространственной системы сил:
åFkx=0; åFky=0; åFkz=0; åMx(Fk)=0; åMy(Fk)=0; åMz(Fk)=0.
Условия равновесия для системы параллельных сил (например, параллельных оси z):
åFkz=0; åMx(Fk)=0; åMy(Fk)=0.
Координаты центра параллельных сил:  .
.
Координаты центра тяжести твердого тела:  ;
;  ; где Р=åрk.
; где Р=åрk.
Центр тяжести плоской фигуры:  ,
,  .
.
Для координаты центра тяжести  плоского тела и для координат центра тяжести
плоского тела и для координат центра тяжести  объемного тела формулы сходные, но в объемном теле суммирование производится по всему объему
объемного тела формулы сходные, но в объемном теле суммирование производится по всему объему  .
.
Центр тяжести тела с вырезанной частью:  . Здесь
. Здесь  – площадь или объем вырезанной части.
– площадь или объем вырезанной части.
Закон Кулона (закон Амонта – Кулона):  .
.
Сила трения скольжения:  . tgjсц=fсц; tgjтр=f.
. tgjсц=fсц; tgjтр=f.
Сила трения качения (без проскальзывания)  .
.  – радиус трения (определяется упругими свойствами катка и поверхности трения),
– радиус трения (определяется упругими свойствами катка и поверхности трения), 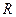 – радиус катка.
– радиус катка.
Кинематика
s=f(t) – естественный способ задания движения, прямолинейное движение: х=f(t).
Координатный способ: x=f1(t), y=f2(t), z=f3(t). Уравнение траектории: f(x,y,z)=0.
Векторный способ: радиус-вектор  =
=  , модуль
, модуль  , направляющие косинусы:
, направляющие косинусы:  и т.д. Переход от координатного способа к естественному:
и т.д. Переход от координатного способа к естественному:  . Скорость точки. Вектор скорости:
. Скорость точки. Вектор скорости:  ;
;  . Проекции скорости:
. Проекции скорости:  ,
,  ,
,  . Модуль скорости:
. Модуль скорости:  , направляющие косинусы:
, направляющие косинусы:  и т.д.
и т.д.
Естественный способ:  ,
,  ,
,  – орт касательной. Движение в полярной системе координат: r=r(t) – полярный радиус, j=j(t) – угол. Проекции скорости на радиальное направление
– орт касательной. Движение в полярной системе координат: r=r(t) – полярный радиус, j=j(t) – угол. Проекции скорости на радиальное направление  , поперечное направление
, поперечное направление  , модуль скорости
, модуль скорости  .; x=rcosj, y=rsinj. Ускорение точки.
.; x=rcosj, y=rsinj. Ускорение точки.  . Проекции уск.-я:
. Проекции уск.-я:  и т.д.
и т.д.
Модуль ускорения: 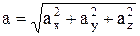 , направляющие косинусы:
, направляющие косинусы: 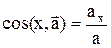 , и т.д.
, и т.д.
Проекции ускорения. на радиальное направление  , поперечное направление
, поперечное направление  , модуль ускорения
, модуль ускорения  .
.  . Модуль нормального ускорения:
. Модуль нормального ускорения:  , r – радиус кривизны траектории, модуль касательного ускорения
, r – радиус кривизны траектории, модуль касательного ускорения  ,
,  ^
^ 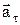 , Þ
, Þ  .
.
Частные случаи движения:
1. Прямолинейное движение: r= ¥, аn=0, a=at.
2. Равномерное криволинейное движение: v=const, at=0, a=an. s=s0+v×t.
3. Равномерное прямолинейное движение: а=at=an=0.
4) Равнопеременное криволинейное движение: at=const, v=v0+at×t,  .
.
Для вращательного движения:
Угловая скорость:  ,. Угловое ускорение тела:
,. Угловое ускорение тела:  .
.
Равномерное вращение: w=const, j=wt, w=j/t, равнопеременное вращение: w=w0+et;  . Скорости и ускорения точек вращающегося тела:
. Скорости и ускорения точек вращающегося тела:  .
.
v=w×r×sin(a) = w×(ОM), (ОМ) – расстояние от точки М до оси вращения.
Формулы Эйлера:  ,
,
vx=wyz – wzy; vy=wzx – wxz; vz=wxy – wyx. Если ось вращения совпадает с осью z, то vx= – wy; vy=wx. Ускорение:  . Вращательное уск.
. Вращательное уск.  , авр=e×r×sina, центростремительное уск.
, авр=e×r×sina, центростремительное уск.  , ац=w2×R. Полное ускорение:
, ац=w2×R. Полное ускорение:  . Угол, между полным и центростремительным ускорениями:
. Угол, между полным и центростремительным ускорениями:  .
.
Плоское движение твердого тела, уравнения плоского движения: xA= f1(t), yA= f2(t), j = f3(t).
Скорость  ;
;  , vBA= w×BA, vAcosa = vBcosb.
, vBA= w×BA, vAcosa = vBcosb.
Мгновенный центр скоростей – Р:  .
.  ,
,  .
.
Ускорения:  ,
,
 .
.  ,
,  ,
,  ,
, 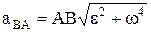 .
.
Мгновенный центр ускорений – Q;  ,
,  ,
,  .
.
Динамика
Основной закон динамики (2-ой закон (Ньютона)):  . Дифференциальные уравнения движения материальной точки:
. Дифференциальные уравнения движения материальной точки: 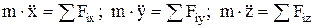 ,
,
 – дифференциальное уравнение прямолинейного движения точки, его общее решение:
– дифференциальное уравнение прямолинейного движения точки, его общее решение:
x=f(t,C1,C2), начальные условия: t=0, x=x0,  =Vx=V0.
=Vx=V0.
 – количество движения материальной точки,
– количество движения материальной точки,  – элементарный импульс силы.
– элементарный импульс силы.
теорема об изменении количества движения материальной точки в дифференциальной форме  , или
, или 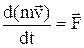 .
. 
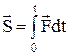 – импульс силы за [0,t]. В проекциях на оси координат:
– импульс силы за [0,t]. В проекциях на оси координат:  и т.д.
и т.д.
 - момент количества движения материальной точки относительно центра О.
- момент количества движения материальной точки относительно центра О.
Теорема об изменении момента количества движения матер. точки.  ,
,  .
.
Если МО= 0, Þ  =const.
=const.  =const, где
=const, где  – секторная скорость. Элементарная работа dA = Ftds, Ft – проекция силы на касательную к траектории, или dA = Fdscosa. dA=
– секторная скорость. Элементарная работа dA = Ftds, Ft – проекция силы на касательную к траектории, или dA = Fdscosa. dA=  – скалярное произведение; dA= Fxdx+Fydy+Fzdz.
– скалярное произведение; dA= Fxdx+Fydy+Fzdz.
Работа силы на любом конечном перемещении М0М1:
 . Если F=const, то
. Если F=const, то  = F×s×cosa.
= F×s×cosa.  ,
,  .
.
Работа силы тяжести:  . A>0, если М0 выше М1.
. A>0, если М0 выше М1.
Работа силы упругости:  .
.
Работа силы трения:  , Fтр=fN. Сила притяжения (тяготения):
, Fтр=fN. Сила притяжения (тяготения):  , k=gR2. Работа силы тяготения:
, k=gR2. Работа силы тяготения:  .
.
Мощность  . Если N=const, то N=A/t.
. Если N=const, то N=A/t.
Теорема об изменении кинетической энергии точки. В дифференциальной форме:  .
.  – кинетическая энергия материальной точки. В конечном виде:
– кинетическая энергия материальной точки. В конечном виде:  .
.
Примеры решения задач
Задача 1.
К одному из узлов плоской фермы приложена сила  . Определить реакции опор фермы и усилия во всех её стержнях.
. Определить реакции опор фермы и усилия во всех её стержнях.
| Дано: P = 8 кН | Решение
1) Определение реакций опор. Внешние силы, приложенные к ферме:  , ,  и и  ; их линии действия должны пересекаться в одной точке (D). Треугольник сил ; их линии действия должны пересекаться в одной точке (D). Треугольник сил  , ,  , ,  подобен треугольнику ADО. Получаем: подобен треугольнику ADО. Получаем:
|
| RA, RB, Si, 1 ≤ i ≤ 10 |

 , где
, где 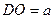 ,
,  ,
,  .
.
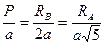
 RB = 16 кН;
RB = 16 кН;  = 17.88 кН.
= 17.88 кН.
2) Определение усилий в стержнях. На каждый узел фермы действуют реакции сходящихся в нём стержней. Эти реакции равны усилиям в стержнях. Рассмотрим равновесия сил, приложенных к узлам, выбирая узлы такой последовательности, чтобы число неизвестных сил в узле не превышало двух. Пусть все стержни растянуты. Отрицательные значения найденных реакций показывают, что соответствующие стержни сжаты. Рассматривая равновесие узлa B получаем, что  .
.
Узел D:  ;
; 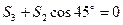

 = –16 кН.
= –16 кН.
 ;
; 

 =22.63 кН
=22.63 кН
Узел O:  ;
; 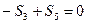

 = -16 кН.
= -16 кН.
 ;
; 

 .
.
Узел C:  ;
; 

 = 11.31 кН.
= 11.31 кН.
 ;
; 

 = -8 кН.
= -8 кН.
Узел A:  ;
; 

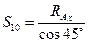 = 11.31 кН.
= 11.31 кН.
 ;
; 

 = 8 кН.
= 8 кН.
Узел K:  ;
; 

 = –8 кН.
= –8 кН.
 ;
;  .
. 
 =-8 кН
=-8 кН
Данные расчёта в таблице:
| Номер стержня | ||||||||||
| Знак усилия | + | + | – | - | + | – | - | + | + | |
| Усилие, кН | 22,63 | 11,31 | 11,31 |
Задача 2.
Найти реакции опор конструкции.

| Дано: G = 10 кН P = 6 кН M = 8 кН∙м α = 45○ | Решение
Рассмотрим равновесную систему сил, приложенных к балке. Заменим связи их реакциями: шарнирно-неподвижную опору A заменим силами XA, YA, нить C заменим силой P, стержневую опору DB заменим силой RB, приложенной в точке D. Составляем уравнения равновесия:
 ; ;  . (1) . (1)
|
| XA, YA, RB –? |

 ;
;  . (2)
. (2)
 ;
;  . (3)
. (3)
(1) 
 = 1,72 кН.
= 1,72 кН.
(2) 
 = 1,22 кН.
= 1,22 кН.
(3) 
 = 2,78 кН
= 2,78 кН
Задача 3.
Найти реакции стержней, поддерживающих тонкую горизонтальную плиту весом G, при действии на неё вдоль AB силы  .
.
Дано: G = 20 кН; P = 25 кН; a = 4 м; b = 5 м; c = 3 м; d = 1,5 м.
Найти: Si –? 1≤ i ≤6.
Решение

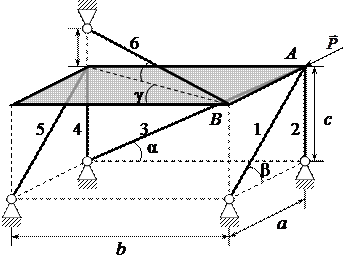
Рассмотрим равновесную систему сил, действующих на плиту. Пусть все стержни растянуты, их реакции  ,
,  ,
,  ,
,  ,
,  ,
,  направлены от углов. Введём углы α, β, γ, θ. Составляем 6 уравнений равновесия:
направлены от углов. Введём углы α, β, γ, θ. Составляем 6 уравнений равновесия:
 ;
;  ; (1)
; (1)
 ;
;  ; (2)
; (2)
 ;
;  ; (3)
; (3)
 ;
;  ; (4)
; (4)
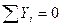 ;
;  ; (5)
; (5)
 ;
;  . (6)
. (6)
Найдём синусы и косинусы углов:
 ;
;  ;
;  ;
;  ;
;
 ;
;  ;
;  ;
; 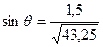 .
.
(2) 
 = 42,69 кН;
= 42,69 кН;
(3) 
 = 32,46 кН;
= 32,46 кН;
(1) 
 = –29,47 кН;
= –29,47 кН;
(5) 
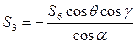 = –37,85 кН;
= –37,85 кН;
(4) 
 = 39,36 кН;
= 39,36 кН;
(6) 
 = 25,68 кН.
= 25,68 кН.
Задача 4.
Найти координаты центра тяжести плоской фигуры
Решение
Разобьём площадь фигуры отрезками LC, KM, SH, GQ по пять прямоугольников. Координаты центра тяжести будем искать по формулам:
 ;
;  . (1)
. (1)


Для фигуры 1 получаем:
F 1 = 4 ∙ 2 = 8 см2; x 1 = 8 – 2/2 = 7 см; y 1 = 10 – 4/2 = 8 см.
Для фигуры 2:
F 2 = 2 ∙ 6 = 12 см2; x 2 = 6/2 = 3 см; y 2 = 10 – 2/2 = 9 см.
Для фигуры 3:
F 3 = 2 ∙ 8 = 16 см2; x 3 = 2/2 = 1 см; y 3 = 8/2 = 4 см.
Для фигуры 4:
F 4 = 10 ∙ 2 = 20 см2; x 4 = 2 + 10/2 = 7 см; y 4 = 2/2 = 1 см.
Для фигуры 5:
F 5 = 4 ∙ 2 = 8 см2; x 5 = 12 – 2/2 = 11 см; y 5 = 4/2 = 2 см.
Составляем таблицу:
| Номер элемента | Fi, см2 | xi, см | yi, см | Six = Fixi, см3 | Siy = Fiyi, см3 |
| Σ | – | – |
По формулам (1) вычисляем координаты центра тяжести плоской фигуры:
 = 5,25 см;
= 5,25 см;  = 4,25 см.
= 4,25 см.
Задача 5.
По заданным уравнениям движения точки M установить вид её траектории и для момента времени t = t 1 найти положение точки на траектории, её скорость, полное, касательное и нормальное ускорение, а также радиус кривизны траектории в соответствующей точке.
Дано:
 (1)
t 1 = 1 c (1)
t 1 = 1 c
| Решение
Уравнения движения (1) являются параметрическими уравнениями траектории точки M. Чтобы получить уравнение траектории в координатной форме, исключим время t из уравнений движения. Тогда:
   . .
|
| v, w, w τ, w n, R –? |
Это уравнение параболы.
Для определения скорости точки находим проекции скорости на оси координат:
 (см/с);
(см/с);  (см/с).
(см/с).
Модуль скорости точки
 .
.
Аналогично проекции ускорения точки
 (см/с2);
(см/с2);  (см/с2).
(см/с2).
Модуль ускорения точки
 = 8 см/с2.
= 8 см/с2.
Координаты точки, её скорость, ускорение и их проекции на координатные оси для момента времени t = 1 с приведены в таблице.
| Координаты, см | Скорость, см/с | Ускорение, см/с2 | Радиус кривизны, см | |||||||
| x | y | vx | vy | v | w x | w y | w | w τ | w n | R |
| –3 | –3 | –8 | –3 | 8,54 | –8 | 7,49 | 2,81 | 28,71 |
Касательное ускорение равно:
 ;
;
 .
.
При t = 1 с
 = 7,49 см/с2.
= 7,49 см/с2.


 .
.
Нормальное ускорение точки:
 = 2,84 см/с2.
= 2,84 см/с2.
Радиус кривизны траектории в данной точке:
 = 28,71 см/с2.
= 28,71 см/с2.
Полученные значения wτ, wn и R также приведены в таблице.
Задача 6.
По заданному уравнению прямолинейного поступательного движения груза 1 определить скорость, вращательное и центростремительное и полное ускорение точки М механизма в момент времени, когда путь, пройденный грузом, равен S.
Решение
1) Найдём момент времени T, когда путь S, пройденный грузом равен 40 см:
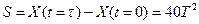

 (с)
(с)
Скорость груза равна:  см/с
см/с

2) Угловая скорость звена 2:  с-1.
с-1.
Угловые скорости колес 2 и 3, связанных гибкой передачей, обратно пропорциональны радиусам этих колес:
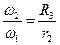

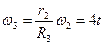 с-1.
с-1.
Угловое ускорение  4 с-2 –
4 с-2 –  .
.
Скорость точки M:  , и направлена перпендикулярно к радиусу в сторону вращения колеса 3) Вращательное ускорение точки M:
, и направлена перпендикулярно к радиусу в сторону вращения колеса 3) Вращательное ускорение точки M:  = 60 м/с2 и направлено в сторону вращения колеса перпендикулярно радиусу колеса.
= 60 м/с2 и направлено в сторону вращения колеса перпендикулярно радиусу колеса.
Центростремительное ускорение точки M:  м/с2.
м/с2.
Полное ускорение:  .
.
Значения этих величин для момента времени  приведены в таблице:
приведены в таблице:
| ω3, с-1 | ε3, с-2 | v, см/с | Ускорение, см/с2 | ||
| aτ | an | a | |||
| 247,38 |
Задача 7.
Найти для заданного положения механизма скорости и ускорения точек B и C.
Дано:
OA = 25 см
АВ = 80 см
АС = 20 см
 = 1 с-1 = 1 с-1
 = 2 с-2 = 2 с-2
| Решение
1. Определение скоростей точек.
Найдём скорость точки A:  = 25 см/с. = 25 см/с.
 , ,  .
Мгновенный центр скоростей находится в точке .
Мгновенный центр скоростей находится в точке  , потому что она находится в точке пересечения перпендикуляров, проведённых из точек A и B к их скоростям. Угловая скорость звена AB: , потому что она находится в точке пересечения перпендикуляров, проведённых из точек A и B к их скоростям. Угловая скорость звена AB:
 = 0,625 (с-1). = 0,625 (с-1).
|
 , ,  , ,
 , ,  –? –?
|
Скорости точек B и C:
 86,6 (см/с).
86,6 (см/с).
 = 106,8 (см/с).
= 106,8 (см/с).
 .
.
2. Определение ускорений точек.
Ускорение точки складывается из вращательного и центростремительного ускорений:
 .
.
 = 50 см/с2;
= 50 см/с2;  = 25 см/с2.
= 25 см/с2.
По теореме об ускорениях точек плоской фигуры имеем:

 или
или 
где  = 50 (см/с2).
= 50 (см/с2).
Строим многоугольник ускорений. Относительно координатных осей получаем
 .
.
Отсюда получаем:  = 8,3 (см/с2);
= 8,3 (см/с2);
 0,195 (с-2).
0,195 (с-2).
Аналогично для точки C:
 или
или
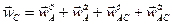
где  = 12,5 (см/с2).
= 12,5 (см/с2).
 = 3,9 (см/с2).
= 3,9 (см/с2).
Значения этих величин для времени  сведены в таблице
сведены в таблице
| ω3, с-1 | ε3, с-2 | v, см/с | Ускорение, см/с2 | ||
| wв | wц | w | |||
| 247,38 |
Задача 8.
Камень скользит в течение τ с по участку AB откоса, составляющему угол α с горизонтом и имеющему длину l. Его начальная скорость vA. Коэффициент трения скольжения камня f. Со скоростью AB и через TC ударяется в т. C о вертикальную стенку.
| Дано: | Решение
Для ускоренно движущегося по плоскости AB тела характерно:
 ; (1) ; (1)
 . (2) . (2)
|
| α = 15○; L = 3 м | |
| vB = 3 м/с; f = 0 | |
| τ = 1,5 с; d = 2 м | |
| vA, h –? |
Делим (1) на (2) и получаем:






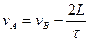 = 4 – 3 = 1 м/с.
= 4 – 3 = 1 м/с.
Для падающего с начальной скоростью vB тела под углом к горизонту характерно:
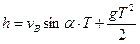 ; (3)
; (3)
 . (4)
. (4)
(4) 
 – (3)
– (3) 
 .
.
Получаем:
 = 0,48 + 2,18 = 2,66 м
= 0,48 + 2,18 = 2,66 м
Задача 9.
Найти уравнение движения тела M массой m, принимаемого за материальную точку и находящегося под действием переменной силы  при заданных начальных условиях.
при заданных начальных условиях.
| Дано: | Решение
Дифференциальное уравнение движения точки M (второй закон Ньютона):
   .
Решим это дифференциальное уравнение.
Так как .
Решим это дифференциальное уравнение.
Так как  , то , то
|

| |
| m = 0,1 кг | |
| z 0 = 200 м | |
 = 0,1 м/с = 0,1 м/с
| |
| z (t) –? |
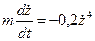







 ;
;
 .
.
Так как  , то
, то




 .
.
Постоянные интегрирования найдём из начальных условий:


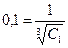

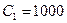 ;
;




 .
.
Окончательно получаем

Задача 10.
Механическая система под действием сил тяжести приходит в движение из состояния покоя. Учитывая скольжение тела A, пренебрегая другими силами сопротивления и массами нитей, определить скорость тела A в момент, когда пройденный им путь станет равным S.

Дано:


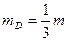
 м м


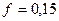

 м м
| Решение
По теореме об изменении кинетической энергии системы:
 ,
где ,
где  и и  – кинетическая энергия системы в конечном и начальном положениях. Пусть – кинетическая энергия системы в конечном и начальном положениях. Пусть  , тогда , тогда  .
Кинетическая энергия системы равна: .
Кинетическая энергия системы равна:
 ,
где ,
где
 – кинетическая энергия груза A. – кинетическая энергия груза A.
 – кинетическая энергия груза A. – кинетическая энергия груза A.
|
| S –? |
 ,
, 

 .
.
 – кинетич. энергия поступательного и вращательного движения барабана D.
– кинетич. энергия поступательного и вращательного движения барабана D.
 ,
,  ,
, 

 .
.
Найдём сумму работ  , приложенных к системе на заданном её перемещении:
, приложенных к системе на заданном её перемещении:
 ,
,
где  ,
,