Анализ устойчивости исходной САР.

Основным моментом анализа исходной САР является установление факта устойчивости системы. Если она неустойчива, то она только по этой причине уже требует коррекции. При устойчивой исходной САР требуется проверка удовлетворения динамических и точностных требований предъявляемых к ней.

Для оценки устойчивости систем используются алгебраические критерии Гурвица и Рауса и частотные методы Михайлова и Найквиста. Принцип всех критериев основан на анализе корней характеристического уравнения, на наличие нулевых и действительных корней, а также комплексных корней, имеющих положительную действительную часть.

Критерий Гурвица.

Формулировка критерия: система автоматического регули­рования устойчива, если все коэффи­циенты однородного дифференциального уравнения замкнутой системы имеют оди­наковый знак, а все определители Гур­вица больше нуля. Пусть характеристическое уравнение замкнутой системы имеет вид

. (1)

Для коэффициентов уравнения (1) составляют квадратную матрицу, содержащую n строк и m столбцов. По диагонали от левого верхнего до правого нижнего углов выписывают все коэффициенты от a_{n- 1} до a ₀. Каждую строчку дополняют коэффициентами с убывающими слева направо индек­сами так, чтобы чередовались строки с нечетными и четными индексами. В случае отсутствия данного коэффициента и если его номер больше п или меньше нуля, на его месте проставляют нуль.

 

. (2)

 

Определители Гурвица составляют по следующему правилу (в соответствии с пунктирными линиями):

; (3)

 

; (4)

 

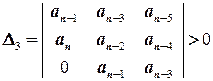. (5)

Последний (n -ый) определитель включает всю матрицу (2), но он может быть выражен через предпоследний определитель Гурвица (D_n-1):

 

. (6)

Так как в устойчивой системе D_n-1 > 0, то положительность последнего определителя сводится к положительности свободного члена характеристического уравнения a₀.

В рассмотренном выше примере передаточная функция разомкнутой системы слежения за соотношением углов поворота приводов главного движения и подачи (рис. 6) имеет следующий вид:

 

. (7)

Для этого случая передаточная функция замкнутой системы

 

, (8)

где – коэффициент усиления разомкнутой системы.

Характеристическое уравнение имеет вид

 

. (9)

Пусть параметры системы имеют следующие значения: К_У1 =1.0; К_У2 =10; К_ТР =10; К_Д =1.26 рад/с×В; К_Дос =1.0 В/рад; Т_ТР =0.003с; Т_Я =0.05с; Т_М =0.15с. Тогда К_р =126 с^-1.

 

В соответствии с критерием Гурвица его определители соответственно равны

 

;

 

 

Поскольку третий и четвертый определители системы меньше нуля, то замкнутая система не устойчива.

 

Критерий Михайлова.

Вектор Михайлова, построенный на основании характеристического уравнения замкнутой системы (1) заменой р = jw, описывает на комплексной плоскости годограф Михайлова.

. (10)

Формулировка критерия: система автоматического регулирования устойчива, если годограф Михайлова начинается при w = 0 на положительной действительной полуоси и с увеличением частоты от 0 до ¥ проходит в положите льном направлении (против часовой стрелки) последовательно, нигде не обращаясь в нуль, п квадрантов (п –порядок диф­ференциального урав­нения системы).

Проверим полученное ранее заключение о не устойчивости системы рис.6 с помощью критерия Михайлова. В соответствии с (9)

 

. (11)

Подставляя в (11) соответствующие числовые значения получим

 

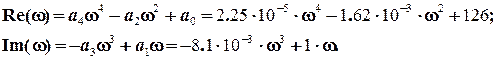
На основании полученных зависимостей можно построить годограф Михайлова на комплексной плоскости (рис.7)

Im(w)

Re(w)

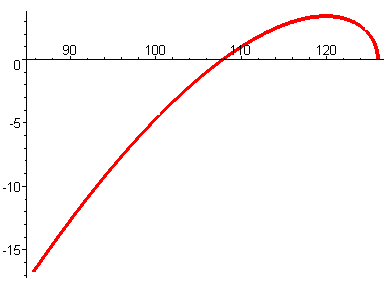
Рис.7. Годограф Михайлова для системы слежения за соотношением углов поворота приводов главного движения и подачи

Из анализа поведения годографа видно, что нарушена последовательность обхода квадрантов. Он не прошел через 2-й квадрант, хотя порядок системы равен 4. Это подтверждает ранее полученное заключение о неустойчивости рассматриваемой системы.

 

 

Критерий Найквиста.

Отличие частотного критерия Найквиста перед критерием Михайлова является то, что он позво­ляет судить об устойчивости замкну­той автоматической системы регу­лирования по характеристикам ра­зомкнутой системы и может быть применен для систем с транспорт­ным запаздыванием без поправок и дополнений.

Формулировка критерия: си­стема автоматического регулирования, устойчивая или нейтрально устойчивая в разомкнутом со­стоянии, устойчива в замкнутом состоянии, если годограф комплексной частотной характеристики (АФХ) разомкнутой системы при изменении ча­стоты от 0 до ¥ не охватывает на комп­лексной плоскости точку с координа­тами (-1; j 0) или охватывает ее на угол kp, где k число корней в правой полуплоскости комплексной плоскости. Для неустойчивой в разомкнутом состоянии системы формулировка критерия несколько сложнее и здесь не рассматривается.

Комплексная частотная характеристика системы может быть получена путем замены р = jw в передаточной функции разомкнутой системы. Она представлена следующим образом

 

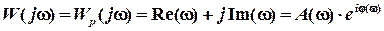. (12)

Для системы с передаточной функцией (7)

 

.

Тогда для алгебраической формы записи годографа

 

 

На основании полученных выражений любым из известных методов, например с помощью пакета программ Mapl или в ручную, можно построить в комплексной плоскости соответствующий годограф (см. рис. 8). Диапазон изменения частоты следует выбирать исходя из значений постоянных времени, например 1/Т₁<w<1/T₃.

Из анализа годографа Найквиста видно, что он охватывает точку с координатами (-1, j0). Это подтверждает ранее полученное заключение о неустойчивости рассматриваемой системы.

 

 

Im(w)

Re(w)

Рис.8. Годограф Найквиста для системы слежения за соотношением углов поворота приводов главного движения и подачи

Критерий, основанный на логарифмических

частотных характеристиках

В практике расчета простых одномерных стационарных систем, являющихся объектом исследования данной контрольно-курсовой работы, широкое распространение получили инженерные методы, основанные на использовании логарифмических частотных характеристик (ЛЧХ) [1 - 3, 5 - 8]. Эти методы позволяют в процессе синтеза корректирующего устройства определить как его структуру, так и параметры. Они снабжены большим количеством удобных номограмм, графиков и зависимостей, позволяющих быстро производить приближенный анализ и синтез линейных САУ.

Пусть, например, требуется провести анализ исходной системы (рис.5), например, с помощью частотного метода, основанного на логарифмических частотных характеристиках системы [6]. Передаточная функция разомкнутой системы примет вид

 

(13)

 

Пусть параметры системы имеют следующие значения: К_У1 =1.0; К_У2 =10; К_ТР =10; К_Д =1.26 рад/с×В; К_Дос =1.0 В/рад; Т_ТР =0.003с; Т_Я =0.05с; Т_М =0.15с. Тогда К_р =126.

Построенная в асимптотах ее логарифмическая амплитудно- фазо-частотная характеристика (рис. 9) позволяет сделать вывод, что система минимально-фазовая с разомкнутой частью, находящейся в близи границы устойчивости, запасы по модулю и фазе отсутствуют L₁(w). Это требует проведения соответствующей коррекции. Интересно заметить, что уменьшение коэффициента усиления до К_р =12 приводит ее в устойчивое состояние (L₂(w)) с запасами по модулю DL=15.6 дБ и по фазе j= 32°. Однако, как будет показано ниже (п. 5.2) в результате этого снижается точность регулирования до с₀=1(1+К_р)=0.077, что является совершенно не допустимым.

 

 

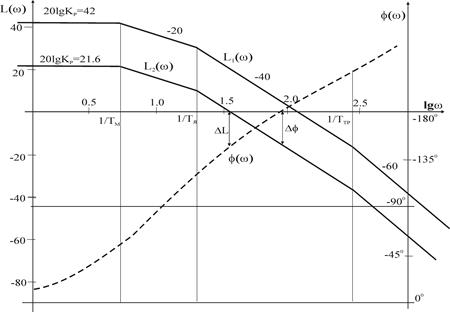
Рис. 9. Логарифмические частотные характеристики исходной разомкнутой системы в асимптотах

 

Несколько более высокую точность позволяет получить построение ЛАЧХ с помощью прикладных пакетов программ, например Mapl, для статической системы с К_р =126 см. рис.10.

Рис. 10. Логарифмические частотные характеристики исходной разомкнутой системы