ПРОЕКТНО-ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
ПО ТЕМЕ
"Простое решение "непростой" задачи"
Автор Кравчук Владимир, 9 класс
ГУО" СШ №2 г. Иваново"
Научный руководитель –
Хлус Ирина Леонидовна,
Учитель математики первой
Квалификационной категории
Уч.год
ОГЛАВЛЕНИЕ
| Введение................................................ | |
| Актуальность темы.................................... | |
| Цель................................................ | |
| Задачи............................................... | |
| Объект исследования.................................. | |
| Предмет исследования................................. | |
| Гипотеза............................................. | |
| Ход работы........................................... | |
| Задача 1................................................. | |
| Решение 1 (арифметическое)............................ | |
| Решение 2 (алгебраическое)............................. | |
| Решение 3 (с помощью графика)......................... | |
| Задача 2................................................. | |
| Задача 3................................................. | |
| Текстовые задачи в тесте................................... | |
| Краткие решения некоторых задач........................... | |
| Задача 3.............................................. | |
| Задача 5.............................................. | |
| Задача 7.............................................. | |
| Результаты тестирования................................... | |
| Выводы.................................................. | |
| Практическая значимость................................... | |
| Литература............................................... |
Введение
Актуальность темы связана с необходимостью выработки навыка быстрого решения текстовых задач в условиях ограниченного времени при различных видах контроля знаний учащихся, например, тестирования.
Цель: Изучить графический метод решения текстовых задач, сравнить его с другими методами (арифметическим (по действиям) и алгебраическим
(с помощью уравнений, неравенств и их систем)
Задачи:
1. провести сравнительный анализ различных методов решения текстовых задач на примере типичной (тестовой) задачи;
2. отработать приемы применения графического метода на серии задач;
3. подобрать примеры текстовых задач в тестах;
4. обучить этому методу учащихся 9 класса;
5. провести исследование преимуществ данного метода.
6. провести тестирование в 9 классе с использованием этого метода;
7. провести анализ результатов;
8. создать компьютерную презентацию.
Объект исследования: Текстовые задачи.
Предмет исследования: Графический метод решения текстовых задач.
Гипотеза: Графический метод решения текстовых задач является более рациональным для выполнении тестовых заданий и имеет большое значение для повышения математической культуры учащихся.
Ход работы.
В ходе работы были изучены графические методы решения текстовых задач. Проведён сравнительный анализ различных методов решения текстовых задач на примере типичной (тестовой) задачи. Отработаны приемы применения графического метода на серии задач Проведено тестирование в 9 классе с использованием этого метода. Сделан анализ результатов. Иллюстративный материал к задачам сделан в среде «Живая математика».
Графическое представление условия задачи может помочь в решении задач различных уровней сложности. С помощью графиков рационально решаются задачи, в которых описывается некоторый процесс: движение, работа, заполнение зала зрителями, горение свечи и так далее.
В школьных задачах, как правило, описываются процессы с постоянной скоростью протекания. Поэтому, независимо от вида процесса, его характеристики связаны одной и той же линейной зависимостью: результат процесса равен произведению скорости и времени его протекания. Формулы этой зависимости имеют вид: S=v, A=vt. График такой зависимости удобно изображать в системе координат: горизонтальная ось – ось времени, вертикальная – ось результата процесса (например, пройденный путь).
Графиком линейной зависимости служит прямая. Угол наклона прямой к оси абсцисс характеризует скорость процесса, а модуль тангенса этого угла численно равен значению скорости протекания процесса.
Изображая графики процессов, можно находить зависимости между величинами, применяя геометрические знания, а можно решать задачу привычным способом. Построенная модель зависимости между величинами помогает увидеть отношения между этими величинами. На этих двух подходах основано использовании графиков при решении текстовых задач.
Задачи приведенные дальше будут решены графическим методом, с достаточно подробным чертежом, описанием решения.
В данной проектной работе я использовал программу Живая математика, при помощи которой удобно стоить чертежи. Используя данную программу, мы можем строить, изменять, видеть непосредственные чертежи задач. Все далее приведенные построения осуществлялись в среде Живой математики.
Задача 1
Грибник и рыболов находятся на расстоянии 220 метров от охотника. Когда охотник догнал грибника, рыболов отставал от них на 180 метров. На каком расстоянии от рыболова был грибник, когда охотник догнал рыболова?
Приведем три решения этой задачи.
Решение 1 (арифметическое)
Обозначим через vор скорость сближения охотника с рыболовом, через vог – скорость сближения охотника с грибником. Сначала рассмотрим движение с момента, когда охотник был на расстоянии 220 метров от грибника и рыболова. Когда охотник догнал грибника, он преодолел разность расстояния между ними, равную по условию 220 метров, а также разность расстояния между ним и рыболовом, обогнав при этом последнего на 180 метров. Таким образом, скорости vог соответствует путь в 220 метров, а скорости vор – 400 метров (220+180). Таким образом 
.
Теперь рассмотрим движение с момента встречи охотника и рыболова. Когда охотник догнал грибника, он преодолел разность расстояния между ними, то есть искомое расстояние, а также обогнал рыболова на 180 метров. Значит, скорости vог соответствует искомый путь, скорости vор – равный 180 метров. Таким образом, когда охотник догнал рыболова, рыболов и грибник были на расстоянии 
.
Ответ: 99 метров.
Решение 2 (алгебраическое)
Обозначим через vо, vг, vр скорости охотника, грибника и рыболова соответственно. Тогда время за которое охотник догнал грибника, равно 
. За это время рыболов и грибник прошли соответственно 
, 
- количество пути, после чего расстояние между ними было 
, что по условию равно 180 метрам. Таким образом, имеем уравнение 
(1).
Рассуждая аналогично, получим, что расстояние между рыболовом и грибником в момент, когда охотник догнал рыболова, было равно 
(2).
Из уравнения (1) выразим vр: 
, и подставим его значение в выражение (2): 
Ответ: 99 метров.
Решение 3 (с помощью графика):
В прямоугольной системе координат построим графики движений грибника, рыболова и охотника (считаем, что они идут с постоянными скоростями). На чертеже точки пересечения графиков соответствуют встречи объектов в какой-то момент времени. Для любой точки графика с координатами (x;y) x – это момент времени, в который объект находится на расстоянии y от начальной точки.
В данной задаче за начальную точку возьмем точку, в которой находился охотник, когда он был на расстоянии 220 метров от рыболова и грибника. Здесь OA=220 метров, CD=180 метров, BE – искомый отрезок (обозначим его за x).
Ход решения:
1) 
OAC~ EBC – по двум углам: 
C – общий, AOC= BEC – как накрест лежащие при параллельных прямых. Из подобия следует:
(1)
2) BAE~ CAD – по двум углам: A – общий, AEB= ADC – как накрест лежащие при параллельных прямых. Из подобия следует:
(2)
3) Сложим уравнения (1) и (2), получим: 
Ответ: 99 метров.
Задача 2
Из пункта O в пункт N вышел пешеход. Одновременно с ним из пункта N в пункт O выехал велосипедист, который встретил пешехода через 50 минут после своего выезда из N. Сколько времени понадобится пешеходу для того, чтобы пройти весь путь, если известно, что велосипедист проделал бы весть путь на 4 часа быстрее пешехода.
Решение:
Построим график зависимости пройденного пешеходом и велосипедистом пути от времени. Пусть p(x) – зависимость пройденного пешеходом пути от времени x, w(x) - зависимость пройденного велосипедистом пути от времени x. Обозначим BC через x. Тогда NK=OB=5/6 ч, CD=4 ч, KT= x, KL= x +4.
Ход решения:
1) MBC ~ MKN – по двум углам: MBC= MKN=90о, KMN= BMC – как вертикальные.
Из подобия следует:
(1)
2) MLK ~ MBO – по двум углам: KLM= MOB – как накрест лежащие углы при параллельных прямых, MBO= MKL=90о. Из подобия следует: 
(2)
3) Из равенств (1) и (2) получаем: 
4) Подставим значения: 
5) Так как OD=(x +5/6+4) – время прохождения пути пешеходом, то он проделал его за 5 часов.
Ответ: 5 часов.
Задача 3
Три пловца должны проплыть из пункта A в пункт B и обратно. Сначала стартует первый, через 5 секунд – второй, еще через 5 секунд – третий. На пути из A до B прошли некоторую точку C одновременно. Третий пловец, доплыв до B и сразу повернув назад, встречает второго в 9 метрах от B, а первого – в 15 метрах от B. Найдите скорость третьего пловца, если расстояние между A и B равно 55 метров.
Решение:
Построим график зависимости пройденного пешеходами и лыжником пути от времени. Пусть p(x) – зависимость пути, который проплыл первый пловец, от времени x, w(x) – зависимость пути, который проплыл второй пловец, от времени x, m(x) – зависимость пути, который проплыл третий пловец, от времени x. AD=DE=5 с, AB=55 м, BT=15 м, BM=9 м.
Ход решения:
1) DKG ~ IKH – по двум углам: DKG= IKH – как вертикальные углы, KDG= KIH – как накрест лежащие при параллельных прямых. Пусть h1, h2 – высоты этих треугольников соответственно. Из подобия следует:
(1)
2) ALG ~ JLH – по двум углам: ALG= JLH – как вертикальные углы, LAG= LJH – как накрест лежащие при параллельных прямых. Пусть h3, h4 – высоты этих треугольников соответственно.
Из подобия следует:
(2)
3) Из равенств (1),(2) следует: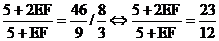 
Следовательно скорость первого пловца: 
Ответ: 1 м/с