Рассмотрим систему линейных однородных уравнений:
(2.5.1)
Система (2.5.1) является частным случаем системы (2.1.1). Она всегда совместна. С одной стороны, это вытекает из теоремы Кронекера–Капелли, так как матрица 
получена из А добавлением нулевого столбца и, следовательно, ранги этих матриц равны. С другой стороны, это видно и непосредственно, так как ей всегда удовлетворяет решение 
, которое будем называть нулевым, или тривиальным. Иногдасистема (2.5.1), кроме тривиального, может иметь и другие решения (нетривиальные). Рассмотрим условия существования нетривиальных решений для данной однородной системы.
Используя теоремы 2.2.2, 2.2.3 и замечание 2.2.1, получим следующие результаты.
Пусть матрица А системы (2.5.1)имеет ранг 
.
Система линейных однородных уравнений (2.5.1) тогда и только тогда имеет единственное нулевое решение, когда ранг ее матрицы равен количеству неизвестных, т. е. r=n.
В частности, если количество уравнений в системе совпадает с числом неизвестных (m=n), то система (2.5.1) имеет единственное нулевое решение тогда и только тогда, когда матрица А невырожденная, т.е. 
.
Для того чтобы система (2.5.1) имела нетривиальные решения, необходимо и достаточно, чтобы ранг матрицы системы был меньше числа неизвестных, т. е. r<n.
Если в однородной системе (2.5.1) число уравнений меньше числа неизвестных (m<n), то она имеет бесконечно много решений.
Все нетривиальные решения системы можно найти, решая систему методом Гаусса, который подробно описан в предыдущем параграфе.
Замечание 2.5.1. В матрице однородной системы (2.5.1) нулевой столбец свободных членов писать не будем. Поэтому вместо матрицы будем писать матрицу А.
Пример 2.5.1. Решить однородные системы уравнений
a)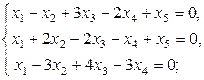 
b) 
Решение:
a)Система состоит из 3-х уравнений, содержащих 5 неизвестных. Данная система является неопределенной, как любая однородная система, в которой число уравнений меньше числа неизвестных. Составим матрицу системы и с помощью элементарных преобразований над строками приведем ее к трапециевидной форме:
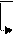
Найдем один из базисных миноров этой матрицы.
Так как 
не существует, то минор 
является базисным. Переменные 
, коэффициенты при которых составляют базисный минор, будем считать базисными, а остальные переменные 
– небазисными, или свободными. Последней матрице соответствует система:
Пусть 
, где 
, тогда 
является общим решением системы.
Ответ: ; 
.
Замечание 2.5.1. Здесь в качестве базисных переменных можно было бы взять переменные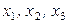 
. Однако вычисления в этом случае будут более громоздкими.
b)
Матрица системы приведена к треугольной форме, следовательно, система имеет единственное тривиальное решение.
Ответ: 
.
Пусть 
– вектор-решения системы (2.5.1), а 
– некоторые числа. Тогда выражение вида 
, согласно определению 1.4.1, является линейной комбинацией вектор-решений системы.
Определение 2.5.1. Вектор-решения называются линейно зависимыми, если хотя бы одно из них является линейной комбинацией остальных. В противном случае, вектор-решения называются линейно независимыми.
Вектор-решения системы линейных однородных уравнений обладает следующими свойствами.
Лемма 2.5.1. Любая линейная комбинация конечного числа вектор-решений системы однородных линейных уравнений (2.5.1) также является вектор-решением данной системы.
В этом несложно убедиться непосредственной подстановкой линейной комбинации вектор-решений в систему.
Лемма 2.5.2. Пусть для системы линейных однородных уравнений (2.5.1) 
, где r – ранг матрицы системы, а n – число неизвестных. Тогда эта система имеет (n–r) линейно независимых вектор-решений таких, что любое другое решение этой системы является их линейной комбинацией.
Доказательство.
Так как в системе (2.5.1) , то данная система имеет n–r свободных неизвестных. Не нарушая общности, можно считать неизвестные 
базисными. Решая систему методом Гаусса, выразим базисные переменные через небазисные
(2.5.2)
Тогда любое вектор-решение этой системы можно записать в виде
(2.5.3)
где 
– произвольные числа; 
определяются равенствами (2.5.2) при условии, что 
.
Рассмотрим вектор-решения системы (2.5.1)
(2.5.4)
Очевидно, что эти вектор-решения линейно независимые. Для любого вектор-решения С системы (2.5.1) имеем 
. То есть, вектор-решение (2.5.3) является линейной комбинацией линейно независимых вектор-решений 
.
Замечание 2.5.1. Можно показать, что (n–r) – максимальное число линейно независимых вектор-решений системы.
Определение 2.5.2. Максимальный набор линейно независимых решенийоднородной системы называется фундаментальной системой решений.
Совокупность решений (2.5.4) является фундаментальной. Эта совокупность называется нормированной фундаментальной системой решений.
Замечание 2.5.2. Для нахождения нормированной фундаментальной системы решений однородной системы с n неизвестными ранга r (r<n) нужно в общее решение системы в качестве значений свободных переменных подставить строки (столбцы) единичной матрицы 
.
Пример 2.5.2. Найти фундаментальную систему решений для системы из примера 2.5.1а.
Решение.
В примере 2.5.1 уже найдено общее решение системы ; . Фундаментальная система решений состоит из 5–3=2 решений. Беря в качестве свободных переменных строки (столбцы) единичной матрицы 
, т.е.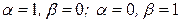 
, получаем вектор-решения
образующие нормированную фундаментальную систему решений.
Ответ: 
.
Пример 2.5.3. Найти фундаментальную систему решений системы
Решение.
В данной системе число уравнений меньше числа неизвестных. Следовательно, система имеет нетривиальные решения. Таким образом, существует фундаментальная система решений указанной системы. Найдем общее решение системы методом Гаусса:
В качестве базисных можно взять переменные 
, так как коэффициенты при этих неизвестных образуют ненулевой определитель 
. Остальные переменные 
– будем считать свободными. Выражая базисные переменные через небазисные, получим
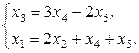
Общее решение системы имеет вид: 
, где 
. Фундаментальная система решений системы состоит из 5–2=3 вектор-решений. Найдем их, беря в качестве свободных переменных элементы строк (столбцов) матрицы 
. Вектор-решения
образуют нормированную фундаментальную систему решений данной системы.
Ответ: 
* Леопольд Кронекер (1823–1891) – немецкий математик, Альфредо Капелли (1855–1891) – итальянский математик. Независимо друг от друга установили критерий совместности произвольной системы линейных уравнений.
* Габриель Крамер (1704–1752) – швейцарский математик. Открыл и опубликовал в 1750 году правило решения систем n линейных уравнений с n неизвестными.
* Карл Фридрих Гаусс (1777–1855) – немецкий математик. В 1849 году в своей работе описал метод последовательного исключения неизвестных для нахождения решений систем линейных уравнений.