Определение 21) Доказать, что не имеет предела в точке (0,0)

Рассмотрим две последовательности точек, сходящихся к (0,0):
(0;  ) и (
) и ( ;0)
;0)
1. 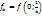 =
=  =-1 и
=-1 и  -1
-1
2.  =
=  =-1 и
=-1 и 
23. f(x,y)= 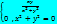 ,
,  +
+  непрерывна в (0,0)?
непрерывна в (0,0)?
24.
(1,0) (Доказать)
25. (Опр) Частной производной функций нескольких переменных по одной их этих переменных называется предел отношения частного приращения функции к приращению соответствует независимой переменной, когда это приращение стремиться к 0.

 =
= 

Ответ:0
26. (определение 25)
Найти частные производные
 =y*2x=4
=y*2x=4
 =
= 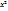 =1
=1
27. Определение дифференцируемости функции. Функция z=f(x,y) называется дифференцируемой в точке ( ,
,  ), если ее полное приращение можно представить в виде:
), если ее полное приращение можно представить в виде:
 =
=  (
(  )
)  , где
, где
 бесконечно малая при
бесконечно малая при 
 - расстояние от (x,y) до (
- расстояние от (x,y) до (  )
)
Если функция z=f(x,y) дифференцируема в ( ), то она непрерывна в этой точке.
), то она непрерывна в этой точке.
Док-во: необходимо проверить, что 
 =
= 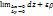 =
=  +
+ 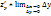 +
+  =0
=0
28. Определение дифференциала функции. Полный дифференциал дифференцируемой функции z=f(x,y) представляет собой главную часть приращения функции, линейную относительно приращения аргументов
dz=  , dx=
, dx= 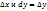
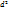 z=
z=  d
d 
Функция z=f(x,y) называется дифференцируемой в точке ( ,
,  ), если ее полное приращение можно представить в виде:
), если ее полное приращение можно представить в виде:
 =
=  (
(  )
)  , где
, где
 бесконечно малая при
бесконечно малая при 
 - расстояние от (x,y) до (
- расстояние от (x,y) до (  )
)
Пример: z=  -?
-?
Как связаны производная по направлению и градиент?
 =(gradf(M),
=(gradf(M),  ) – скалярное произведение векторов
) – скалярное произведение векторов
Произведение по направлению представляет собой скалярное произведение  и вектора с координатами (
и вектора с координатами ( ) (градиент)
) (градиент)
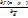 =
=  *
*  *cos
*cos 
Если  , то производная равна 0
, то производная равна 0
Определение градиента. Градиентом функции в т. М называется вектор, координаты которого равны частным производным данной функции в точке М
grad f(M)=( )
)
Градиент указывает направление наискорейшего роста функции
 =(gradf(M),
=(gradf(M),  )=
)=  *
*  *cos
*cos  - достигает наибольшего значения при
- достигает наибольшего значения при
cos  при
при  , т.е. в направлении градиента
, т.е. в направлении градиента
31. Определение однородной функции степени α. Пусть D из Rn – область в Rn, содержащая с каждой своей точкой (x1, x2, …., xn) и все точки вида (tx1, tx2, …., txn) при t>0 функция f(x1, x2, …., xn) с такой областью определения D называется однородной степени λ, если для любого t>0 выполнятся равенство f (tx1, tx2, …., txn)=tλf(x1, x2, …., xn).
Да, является. 2 степени.  =t2
=t2
32. Пример однородной функции степени 3, не являющейся рациональной функцией:
F (x,y)=x2 
F (tx, ty)=t2x2√(tx*ty)=t3F (x,y)
33. Вывести формулу Эйлера для однородной функции трех переменных.
f (tx1, tx2,tx3)=tλf(x1, x2, x3). u= f(x,y,z)
 или, короче,
или, короче,

34. Определение локального экстремума для функции двух переменных. Является ли равенство нулю частных производных функций в некоторой точке достаточным условием ее локального экстремума в этой точке? Пусть z=f(x;y) определена в некоторой области D и точка М(х0;у0) – внутренняя точка D (М принадлежит D), тогда данная функция в данной точке будет иметь локальный минимум (максимум), если найдется e - окрестность точки М, что для всех внутренних точек этой окрестности, отличных от М(х0;у0) выполняются неравенства:
f(x;y)>f(х0;у0) – min или
f(x;y)<f(х0;у0) – max
Нет, т.к. это является необходимым условием.
35. Имеет ли функция f(x,y)=x6y4локальный экстремум в точке (0,0)?
Вводим переменную h так, чтобы g(x,y) = (x-h)6(y-h)4 . Подставляем точку (0,0) – получается, что g = (-h)6 * (-h)4 = h1o – четная, неотрицательная =>экстремум есть. Понятия не имею, откуда это, но Марине я верю.
36.f(x,y)=xy4 (0,0)
Аналогично 35, но там получается g = h5и экстремума нет.
37. f(x.y)=x2-y2 (o,o)
| x=0 y=0 |

 =-4 <0 точек нет Ответ: нет
=-4 <0 точек нет Ответ: нет
38. Доказать, что функция f(x.y)=x2+y2 а) не имеет лок. экстремума в (1,1), б) имеет в этой точке условный локальный экстремум при наличии связи х+у=2
а) F’x=2xF’y=2y
В точке (1,1) первые производные данной функции не обращаются в ноль, следовательно точка (1,1) не является точкой локального экстремума (не выполняется необходимое условие).
б) Дано уравнение связи x+y=2. Y=2-x
f= x2+(2-x)2=2x2-4x+4
f’=4x-4=0 x=1 при х=1 у=2-1=1
39. Найти наименьшее значение функции f(x,y) = |x-1| + 2y2 -3
Рассмотрим 3 случая. 1) х-1>0 2)x-1<0 3) x=0