Вероятность событий. Классическое определение вероятности. Свойства вероятности событий

Вероятность события – численная мера возможности его наступления.

Событие А называется благоприятствующим событию В, если всякий раз, когда наступает событие А, наступает и событие В.

События А ₁, А ₂,..., А_n образуют схему случаев, если они:

1) равновозможны; 2) попарно несовместны; 3) образуют полную группу.

В схеме случаев (и только в этой схеме) имеет место классическое определение вероятности P (A) события А. Здесь случаем называют каждое из событий, принадлежащих выделенной полной группе равновозможных и попарно несовместных событий.

Если n – число всех случаев в схеме, а m – число случаев, благоприятствующих событию А, то вероятность события А определяется равенством:

Из определения вероятности вытекают следующие ее свойства:

1. Вероятность достоверного события равна единице.

Действительно, если событие достоверно, то каждый случай в схеме случаев благоприятствует событию. В этом случае m = n и, следовательно,

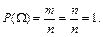
2. Вероятность невозможного события равна нулю.

Действительно, если событие невозможно, то ни один случай из схемы случаев не благоприятствует событию. Поэтому m =0 и, следовательно,

3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Действительно, случайному событию благоприятствует лишь часть из общего числа случаев в схеме случаев. Поэтому 0< m < n, а, значит, 0< m / n <1 и, следовательно, 0 < P(A) < 1.

Итак, вероятность любого события удовлетворяет неравенствам

0 £ P(A) £ 1.

В настоящее время свойства вероятности определяются в виде аксиом, сформулированных А.Н. Колмогоровым.

Одним из основных достоинств классического определения вероятности является возможность вычислить вероятность события непосредственно, т.е. не прибегая к опытам, которые заменяют логическими рассуждениями.

Примеры решения задач

ПРИМЕР 1. Какова вероятность появления четного числа очков (событие А) при одном бросании игрального кубика?

Решение. Рассмотрим события А_i – выпало i очков, i = 1, 2, …,6. Очевидно, что эти события образуют схему случаев. Тогда число всех случаев n = 6. Выпадению четного числа очков благоприятствуют случаи А ₂, А ₄, А ₆, т.е. m = 3. Тогда .

ПРИМЕР 2. В урне 5 белых и 10 черных шаров. Шары тщательно перемешивают и затем наугад вынимают 1 шар. Какова вероятность того, что вынутый шар окажется белым?

Решение. Всего имеется 15 случаев, которые образуют схему случаев. Причем ожидаемому событию А – появлению белого шара, благоприятствуют 5 из них, поэтому .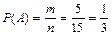

ПРИМЕР 3. Группа из 5 женщин и 20 мужчин выбирает трех делегатов. Считая, что каждый из присутствующих с одинаковой вероятностью может быть выбран, найти вероятность того, что выберут двух женщин и одного мужчину.

Решение. Общее число равновозможных исходов испытания равно числу способов, которыми можно выбрать трех делегатов из 25 человек, т.е. . Подсчитаем теперь число благоприятствующих случаев, т.е. число случаев, при которых имеет место интересующее нас событие. Мужчина-делегат может быть выбран двадцатью способами. При этом остальные два делегата должны быть женщинами, а выбрать двух женщин из пяти можно . Следовательно, . Поэтому

.

Частота событий

Статистическое определение вероятности используется в случае, когда исходы опыта не являются равновозможными.

Относительная частота события А определяется равенством:

,

где m – число испытаний, в которых событие А наступило, n – общее число произведенных испытаний.

Я. Бернулли доказал, что при неограниченном увеличении числа опытов относительная частота появления события будет практически сколь угодно мало отличаться от некоторого постоянного числа. Оказалось, что это постоянное число есть вероятность появления события. Поэтому, естественно, относительную частоту появления события при достаточно большом числе испытаний называть статистической вероятностью в отличие от ранее введенной вероятности.

Пример. Как приближенно установить число рыб в озере?

Пусть в озере х рыб. Забрасываем сеть и, допустим, находим в ней n рыб. Каждую из них метим и выпускаем обратно. Через несколько дней в такую же погоду и в том же месте забрасываем ту же самую сеть. Допустим, что находим в ней m рыб, среди которых k меченных. Пусть событие А – «пойманная рыба мечена». Тогда по определению относительной частоты .

Но если в озере х рыб и мы в него выпустили n меченых, то .

Так как  Р ^*(А) » Р (А), то .