Среди статистических гипотез центральное место занимают гипотезы о равенстве средних.
Эти гипотезы имеют место в случаях, если необходимо обосновать предположение что среднее значение некоторого показателя в двух группах различается или что показатель в одной группе с течением времени под влиянием каких-то факторов в среднем изменился.
Выборки, по которым проверяется гипотеза, называются связанными, если каждому значению одной выборки xi соответствует элемент yi из другой выборки характеризующие показатели для одного и того же тестируемого, но в различных условиях.
Несвязанные выборки как правило характеризуют различные группы респондентов, например экспериментальную группу сравнивают с контрольной.
Параметрический критерий Стьюдента
Это наиболее мощный критерий сравнения средних для связанных и несвязанных выборок объема n и m, однако, он применяется для случаев, когда показатели, представленные выборками имеют закон распределения близкий к нормальному. В основе критерия лежит сравнение основных выборочных параметров (средних и дисперсий), поэтому он называется параметрическим. Рассмотрим случай когда выборки независимы и несвязны.
Рассматриваются две генеральные совокупности  и
и 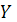 , выборки из них
, выборки из них  .
.
 - средние значения равны.
- средние значения равны. 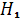 - средние значения различны.
- средние значения различны.
Задается уровень значимости α.
Рассчитывается.
На первом этапе по выборкам вычисляются выборочные средние и дисперсии:
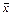 =
= 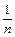 (x1+x2+…+xn),
(x1+x2+…+xn), 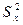 =
= 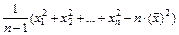 ,
,
 =
= 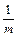 (y1+y2+…+ym),
(y1+y2+…+ym), 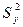 =
=  .
.
На втором этапе сравниваются дисперсии. Для этого вычисляется F = 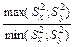 , как отношение большей дисперсии к меньшей. Это число сравнивается с критическим значением
, как отношение большей дисперсии к меньшей. Это число сравнивается с критическим значением  , взятым из приложения 3 по Теме 8. При этом
, взятым из приложения 3 по Теме 8. При этом 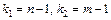 , если
, если 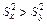 и
и 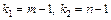 , если
, если 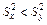 . Если
. Если 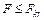 , то дисперсии можно считать равными, если
, то дисперсии можно считать равными, если  , то дисперсии различны.
, то дисперсии различны.
На третьем этапе вычисляется статистика критерия Стьюдента:
 где
где  , (3)
, (3)
если дисперсии равны и
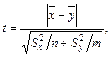 (4)
(4)
если дисперсии различные.
По таблице обратного распределения Стьюдента (ПРИЛОЖЕНИЕ1) находят критическое значение статистики  . Если
. Если 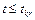 , то средние значения показателей для выборок не различаются.
, то средние значения показателей для выборок не различаются.
Задача. Произведены две выборки урожая пшеницы: при своевременной уборке урожая и уборке с некоторым опозданием. В первом случае измерялась урожайность 14 участков; во втором – 12 участков. Значения урожайности (ц/га) приведены в таблице. На уровне значимости 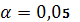 .выяснить влияние своевременности уборки урожая на среднее значение урожайности. Использовать параметрический критерий Стьюдента.
.выяснить влияние своевременности уборки урожая на среднее значение урожайности. Использовать параметрический критерий Стьюдента.
| Урожайность при своевременной уборке урожая | |||||||||||||
| Урожайность при уборке с некоторым опозданием | |||||||||||||
Решение.
Первый этап. Объемы выборок равны n = 14; m = 12. Вычисляем выборочные средние и дисперсии.
 =
=  (x1+x2+…+xn);
(x1+x2+…+xn);
 =
= 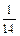 (23+25+23+22+23+24+28+16+18+23+29+26+31+19) = 23,5;
(23+25+23+22+23+24+28+16+18+23+29+26+31+19) = 23,5;
 =
= 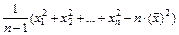 ,
,
 =
=  (232+252+232+222+232+242+282+162+182+ +232+292+262+312+192- 14(23,5)2) = 20,96,
(232+252+232+222+232+242+282+162+182+ +232+292+262+312+192- 14(23,5)2) = 20,96,
 =
=  (y1+y2+…+ym),
(y1+y2+…+ym),
 =
=  (6+27+29+24+17+24+30+33+23+26+20+34) = 25,2,
(6+27+29+24+17+24+30+33+23+26+20+34) = 25,2,
 =
= 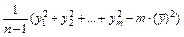 ,
,
 =
= 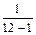 (162+272+292+242+172+242+302+332+232+
(162+272+292+242+172+242+302+332+232+
+262+202+342- 12(25,2)2) = 36,04.
Второй этап. Проверяем, можно ли считать средние равными:
F = 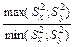 =
= 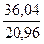 = 1,7,
= 1,7,
По табл. ПРИЛОЖЕНИЯ 3 находим Fкр = F (11; 13) = 2,65.
Видно, что F < Fкр (т.к. 1,7 < 2,65), то есть дисперсии можно считать равными. Исходя из этого на третьем этапе применяем формулу (3).
Третий этап. Вычисляем статистику критерия:
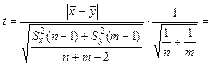
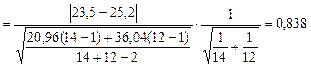 .
.
По табл. Стьюдента (1 ПРИЛОЖЕНИЯ) находим критическое значение критерия:
tкр = t1-a (n+m-2)=t 0,95(24)=1,711
Видно, что t < tкр (т.к. 0,838 < 1,711), следовательно для выборок средние показатели различаются и можно говорить, что для данных выборок показатели агрессивности у мужчин и женщин можно считать статистически равными, а предположение о том, что агрессивность в среднем у мужчин и женщин в данных группах различна отвергается по выборочным данным.
Критерий знаков
Используется только для связанных выборок.
Для его применения выписывают пары значений первой и второй выборок  , затем находят разности между элементами первой и второй выборок в каждой паре
, затем находят разности между элементами первой и второй выборок в каждой паре  и считают число положительных разностей r. При этом l – число ненулевых разностей.
и считают число положительных разностей r. При этом l – число ненулевых разностей.
Если предполагается, что средний показатель первой выборки больше чем у второй, то это предположение можно считать справедливым, если выполняется неравенство:
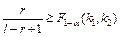 , (1)
, (1)
где k 1=2(l-r +1), k 2=2 r,
Если же предполагается, что средний показатель выше у второй выборке, то это считается справедливым, если выполняется неравенство
 , (2)
, (2)
где k1 =2(r +1), k2 =2(l-r).
Здесь  - обратное распределение Фишера, его значения находят по статистическим таблицам (см. табл. приложения 3).
- обратное распределение Фишера, его значения находят по статистическим таблицам (см. табл. приложения 3).
Если оба неравенства (1)-(2) не выполняются, то значения показателя в обеих выборках в среднем равны.
ЗАДАЧА. Технолог разработал новую технологию, позволяющую, по его мнению, увеличить производительность оборудования. Для проверки этого предположения были измерены показатели 14 оборудований до x и после y внедрения технологии. Можно ли с вероятностью 0,95 говорить о том, что разработанная технология действительно приводит к увеличению производительности, используя критерий знаков.
| x | ||||||||||||||
| y |
Решение. Используем критерий знаков. Присвоим каждой паре значений обоих выборок знаки по следующему правилу:
если xi > yi знак «+ »,
если xi < yi знак «- »,
если xi = yi знак «0».
| xi | ||||||||||||||
| yi | ||||||||||||||
| Знаки | + | + | - | - | + | + | - | - | - | + | - | - |
l = 12 (число ненулевых разностей);
r = 5 (число разностей со знаком «+»);
доверительная вероятность р =0,95, следовательно уровень значимости a=1-0,95=0,05.
Так как предполагается, что средний показатель второй выборки выше, чем средний показатель у первой, то вычисляется левая часть неравенства (2) по формуле:
F =  .
.
Правая часть этого неравенства вычисляется по таблице ПРИЛОЖЕНИЯ 3 по теме:
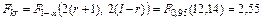 ,
,
Видно, что F < Fkr, то есть можно считать, что средние показатели для выборок из обеих групп статистически не различаются, т.е. методика не привела к увеличению уровня внимательности.
Если выборки являются независимыми и не связаны, то существует несколько критериев решения данной задачи. Рассмотрим основные из них.