Поверхности второго порядка
Понятие алгебраической поверхности
Определение. Алгебраической поверхностью называют множество точек  пространства, координаты которых относительно некоторой аффинной системы координат удовлетворяют уравнению
пространства, координаты которых относительно некоторой аффинной системы координат удовлетворяют уравнению
 , (1.1)
, (1.1)
где  - целая рациональная функция (многочлен) степени
- целая рациональная функция (многочлен) степени  от переменных
от переменных 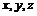 .
.
Степень  называют порядком поверхности.
называют порядком поверхности.
Если уравнение (1.1) не является алгебраическим, то поверхность называют трансцендентной.
Если  , то поверхность первого порядка – плоскость:
, то поверхность первого порядка – плоскость:
 .
.
Если  , то общее уравнение поверхности второго порядка относительно некоторой аффинной системы координат записывают в виде
, то общее уравнение поверхности второго порядка относительно некоторой аффинной системы координат записывают в виде
 (1.2)
(1.2)
причем очевидно, что  .
.
Первые шесть слагаемых уравнения (1.2) называют его старшими членами, а их коэффициенты – старшими коэффициентами.
Для изучения поверхностей используют так называемый метод параллельных сечений.
Определение. Сечениями называют линии пересечения плоскостей с поверхностью.
Для определения формы поверхности по ее уравнению проводят ряд равноотстоящих друг от друга секущих плоскостей, как правило, частного расположения относительно системы координат (плоскостей, параллельных координатным плоскостям). В таком случае сечения называют линиями уровня изучаемой поверхности. Далее линии уровня проецируют на соответствующие координатные плоскости – получают так называемую карту. По форме и расположению линий на карте делают вывод о форме изучаемой поверхности.
Цилиндрические поверхности
Пусть в некоторой аффинной системе координат заданы в плоскости  некоторая линия
некоторая линия  уравнением
уравнением
 (2.1)
(2.1)
и некоторый ненулевой вектор  :
: 
Определение. Множество всевозможных прямых, параллельных вектору  и пересекающих линию
и пересекающих линию  , называют цилиндрической поверхностью.
, называют цилиндрической поверхностью.
Линию  называют при этом направляющей поверхности, а параллельные прямые – образующими.
называют при этом направляющей поверхности, а параллельные прямые – образующими.


(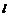 - образующая)
- образующая) 
 .
.
Очевидно, что векторы  и
и  коллинеарны. Следовательно, справедливы соотношения
коллинеарны. Следовательно, справедливы соотношения
 .
.
Отсюда имеем  .
.
Рис. 1. Цилиндрическая поверхность.
Подставляя эти равенства в (2.1), получаем соотношение
 . (2.2)
. (2.2)
Этому равенству удовлетворяют координаты тех и только тех точек, которые лежат на поверхности  . Следовательно, (2.2) – уравнение цилиндрической поверхности.
. Следовательно, (2.2) – уравнение цилиндрической поверхности.
Теорема 2.1. Если образующие цилиндрической поверхности параллельны оси  , то уравнение такой поверхности по внешнему виду совпадает с уравнением ее направляющей.
, то уравнение такой поверхности по внешнему виду совпадает с уравнением ее направляющей.
► Действительно, если  , то
, то  . Тогда соотношение (2.2) равносильно уравнению
. Тогда соотношение (2.2) равносильно уравнению
 , (2.3)
, (2.3)
которое по внешнему виду полностью совпадает с уравнением (2.1) направляющей  . ◄
. ◄
В связи с этим можно дать другое определение цилиндрической поверхности.
Определение. Алгебраическую поверхность называют цилиндрической, если в некоторой аффинной системе координат ее можно задать алгебраическим уравнением, не содержащим одну из координат.
Теорема 2.2. Сечения цилиндрической поверхности параллельными плоскостями, пересекающими ее образующие, принадлежат одному и тому же аффинному классу кривых, к которому принадлежит ее направляющая.
Определение. Цилиндрическую поверхность называют поверхностью второго порядка, если ее направляющей является линия второго порядка.
◊ Для каждого из девяти видов линий второго порядка существует цилиндрическая поверхность с образующими, параллельными одной из координатных осей.
Примеры цилиндрических поверхностей второго порядка.


Рис. 2. Эллиптический цилиндр Рис. 3. Гиперболический цилиндр



Рис. 4. Параболический цилиндр 
Эллипсоид.
Определение. Множество точек  пространства, координаты которых в некоторой прямоугольной декартовой системе координат удовлетворяют уравнению
пространства, координаты которых в некоторой прямоугольной декартовой системе координат удовлетворяют уравнению
 , (3.1)
, (3.1)
называют эллипсоидом.
Будем считать, что  .
.
Из уравнения (3.1) следует, что если на эллипсоиде лежит точка  , то на нем лежат и точки
, то на нем лежат и точки  с любым набором знаков
с любым набором знаков  и
и  . Это означает, что для поверхности (3.1) начало координат – точка
. Это означает, что для поверхности (3.1) начало координат – точка  – является ее центром симметрии и называется центром эллипсоида; оси координат являются осями симметрии и их называют главными осями; координатные плоскости являются плоскостями симметрии и называются главными плоскостями поверхности.
– является ее центром симметрии и называется центром эллипсоида; оси координат являются осями симметрии и их называют главными осями; координатные плоскости являются плоскостями симметрии и называются главными плоскостями поверхности.
Если  , то эллипсоид (3.1) называют трехосным.
, то эллипсоид (3.1) называют трехосным.
Рассмотрим сечения поверхности (3.1) плоскостями, параллельными координатным плоскостям.
1) Сечения эллипсоида плоскостями  определяются уравнениями
определяются уравнениями
 или
или  (3.2)
(3.2)
а) Если 
 , то система (3.2) действительных решений не имеет. Это означает, что плоскость
, то система (3.2) действительных решений не имеет. Это означает, что плоскость  в этом случае не пересекает поверхность (3.1).
в этом случае не пересекает поверхность (3.1).
б) Если 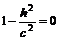
 , то система (3.2) имеет одно единственное решение
, то система (3.2) имеет одно единственное решение  при
при  и одно единственное решение
и одно единственное решение  при
при  .
.
Точки  и
и  пересечения поверхности (3.1) с осью
пересечения поверхности (3.1) с осью  называют вершинами эллипсоида.
называют вершинами эллипсоида.
в) Если 
 , то уравнения (3.2) равносильны системе
, то уравнения (3.2) равносильны системе
 (3.3)
(3.3)
Уравнения (3.3) определяют эллипс, расположенный в плоскости 
 . Его центр находится в точке
. Его центр находится в точке  , оси параллельны координатным осям
, оси параллельны координатным осям  и
и  . Длины полуосей
. Длины полуосей
 и
и 
изменяются от  и
и  до
до 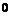 при изменении
при изменении  от
от 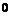 до
до  соответственно. Если
соответственно. Если  , то сечением поверхности (3.1) является самый большой из эллипсов (3.3):
, то сечением поверхности (3.1) является самый большой из эллипсов (3.3):
 (3.4)
(3.4)
2) Сечения поверхности (3.1) плоскостями  и
и  рассматриваются совершенно аналогичным образом. При этом точки
рассматриваются совершенно аналогичным образом. При этом точки  ,
,  и
и  ,
,  пересечения эллипсоида с координатными осями
пересечения эллипсоида с координатными осями  и
и  соответственно также называют вершинами эллипсоида.
соответственно также называют вершинами эллипсоида.
Из приведенных выше рассуждений следует, что эллипсоид целиком расположен внутри параллелепипеда, вершины которого находятся в точках  . Каждая грань этого параллелепипеда имеет с поверхностью (3.1) только одну общую точку – его вершину.
. Каждая грань этого параллелепипеда имеет с поверхностью (3.1) только одну общую точку – его вершину.
Приведенные рассуждения и сделанные при этом выводы позволяют получить представление о форме рассматриваемой поверхности (Рис. 5).

Рис. 5. Эллипсоид.
Если  , то эллипсоид (3.1) называют вытянутым эллипсоидом вращения; он получается вращением эллипса
, то эллипсоид (3.1) называют вытянутым эллипсоидом вращения; он получается вращением эллипса  вокруг его большой оси (Рис. 6).
вокруг его большой оси (Рис. 6).

Рис. 6. Вытянутый эллипсоид вращения.
Если  , то эллипсоид (3.1) называют сжатым эллипсоидом вращения; он получается вращением эллипса
, то эллипсоид (3.1) называют сжатым эллипсоидом вращения; он получается вращением эллипса  вокруг его малой оси (Рис. 7).
вокруг его малой оси (Рис. 7).

Рис. 7. Сжатый эллипсоид вращения.
Если  , то эллипсоид (3.1) является сферой радиуса
, то эллипсоид (3.1) является сферой радиуса  с центром в начале координат (Рис.8).
с центром в начале координат (Рис.8).

Рис. 8. Сфера.