Принцип максимума
Функция U, гармоническая в области 
, достигает своего максимума и минимума только на границе 
. Таким образом, гармоническая функция не может иметь во внутренней точкеобласти локального экстремума, за исключением тривиального случая постоянной в функции. Однако функция может быть неопределена на границе, поэтому правильнее сказать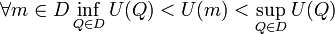 
Теорема Лиувилля
Гармоническая функция, определённая на 
и ограниченная сверху или снизу, постоянна.
Свойство среднего
Если функция 
гармонична в некотором шаре 
с центром в точке 
, то её значение в точке равно её среднему значению по границе этого шара или по шару:
где 
— объём шара и 
— площадь его границы. Обратно, любая функция, обладающая свойством среднего в некоторой области, является в этой области гармонической.
Дифференцируемость
Функция, гармоническая в области, бесконечно дифференцируема в ней.
Амплитуда — наибольшее значение, которое принимает какая-либо величина, изменяющаяся по гармоническому закону[1].
Формальное определение предполагает применение термина "амплитуда" только для гармонической функции; "амплитуда" — модуль коэффициента перед гармонической функцией. В связи с этим термин "амплитуда" следует отличать от терминов, применимых к произвольным функциям:
§ Максимальное значение сигнала — наибольшее мгновенное значение сигнала на протяжении заданного интервала времени
§ Минимальное значение сигнала — наименьшее мгновенное значение сигнала на протяжении заданного интервала времени
§ Размах сигнала — разность между максимальным и минимальным значениями сигнала на протяжении заданного интервала времени
Период электрического тока — Наименьший интервал времени, по истечении которого мгновенные значения периодического электрического тока повторяются в неизменной последовательности.
Круговая частота́ — скалярная физическая величина, мера частоты вращательного или колебательного движения. В случае вращательного движения, угловая частота равна модулю вектора угловой скорости. В системах СИ и СГС угловая частота выражается в радианах в секунду, её размерность обратна размерности времени (радианы безразмерны). Угловая частота является производной по времени от фазы колебания:
Другое распространённое обозначение 
Угловая частота в радианах в секунду выражается через частоту f (выражаемую в оборотах в секунду или колебаниях в секунду), как
В случае использования в качестве единицы угловой частоты градусов в секунду связь с обычной частотой будет следующей:
Численно циклическая частота равна числу циклов (колебаний, оборотов) за 2π секунд. Введение циклической частоты (в её основной размерности — радианах в секунду) позволяет упростить многие формулы в теоретической физике и электронике. Так, резонансная циклическая частота колебательного LC -контура равна 
тогда как обычная резонансная частота 
В то же время ряд других формул усложняется. Решающим соображением в пользу циклической частоты стало то, что множители 2π и 1/(2π), появляющиеся во многих формулах при использовании радианов для измерения углов и фаз, исчезают при введении циклической частоты.
Комплексная синусоида
Комплексная функция: 
облегчает многие виды операций с
использованием, в значительной степени благодаря упрощению Эйлера:
Эта часто употребимая запись называются комплексной синусоидой, и она сохраняет различие между положительными и отрицательными 
.
§ Для положительных значений она так же зовется аналитическим сигналом .
Преобразование Фурье от 
— ненулевой отклик на единственной частоте .
§ Преобразование от имеет отклики на и 
, что отражает тот факт, что одного недостаточно для определения знака .
§ Как, например, 
это +2 или −2, конкретный результат зависит от сопутствующей информации.
§ По-другому, и очень удобно, это показывает следствие из формулы Эйлера, содержащее обе частоты: 
.
Метод компле́ксных амплитуд — метод расчета линейных электрических цепей, содержащих реактивные элементы, в установившемся режиме при гармонических входных сигналах, впервые применённый О. Хевисайдом.
Суть метода заключается в следующем:
§ Для всех реактивных элементов определяется их комплексный импеданс.
§ Все токи и напряжения рассматриваются в виде комплексных амплитуд.
После введения этих замен задача анализа цепи сводится к задаче анализа цепи на постоянном токе:
§ импедансы трактуются как обычные сопротивления
§ комплексные амплитуды токов и напряжений как обычные токи и напряжения
Таким образом, мы избавились от реактивности элементов и зависимости от времени сигналов. Эти факторы, затрудняющие математическое описание схемы, теперь перенесены в сигнал: все параметры зависят от частоты гармонического сигнала и являются комплекснозначными.
Задача анализа цепи на постоянном токе решается соответствующими методами, например, методом узловых потенциалов или методом контурных токов. После нахождения всех искомых комплексных амплитуд их можно при необходимости перевести обратно в гармонические сигналы.
2.7 з-ны Ома и Кирхгофа в компл-ной форме…
Обратимся к законам Кирхгофа для цепи переменного ток
для любого узла 1 –й закон
Для любого контура 2 –й закон
В установившемся гармоническом режиме все токи и напряжения изменяются по гармоническому закону.Составим этим функциям(оригиналы) их комплексы(изображения)
Пользуясь методом комплексных амплитуд перейдем от уравнений связывающих оригиналы к уравнениям связывающим их изображения, тогда вместо уравнения (1) получим
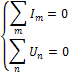
Для любого узла,для любого контура (2)
Законы Кирхгофа в комплексной форме
Перейдем теперь к ур-ям элементов цепи
i(t) R
U(t)=Ri(t)
В установившемся гармоническом режиме, который мы изучаем, все токи и напряжения будут гармоническими. Введем, как и выше отвечающие им изображения
Методом комплексных амплитуд перейдем от уравнений связывающие оригиналы к уравнениям связывающие изображения
Эти 3 рисунка можно объединить в 1 след. образом
Уравнение (3) –называют 3- ом Ома в Комплексной форме
R,JwL, 
- комплексными сопротивлениями или импедансами
Применяют так же след. название,R- активное сопротивление
wL (емкостное сопротивление) 
(емкостное сопротивление)-реактивные сопротивления
все это вещественные величины
С помощью законов Кирхгофа в комплексной форме легко убедиться что остаются справедливыми все правила нахождения общего сопротивления цепи состоящей из нескольких элементов (т.е. правила которыми мы пользовались,изучая цепи постоянного тока)
2.9 расчет эл-х цепей в установившемся гармоническом режиме…
Понятие переходного процесса. Дифференциальное ур-е переходного процесса, тип диф ур-я и его вывод с помощью з-нов Кирхгофа
Рассмотрим эл цепь состоящую из резисторов, катушек, конденсаторов, ист напряжения и ист тока.
Все источники явл-ся либо постоянными либо периодическими, примем период Ту всех ист-ов во 2-м случаем одинаковым.
Будем считать, что рабата ист-ка началась при t=-∞, тогда к моменту времени t=0 в цепи будет иметь место установившийся режим. Это означает, что токи во всех ветвях цепи и напряжения на всех эл-тах будет изменяться во времени по периодическому з-ну с одинаковым для всех величин периодом T. Пусть в момент t=0 в цепи происходит коммутация: включ каких-то источников, или подключ новых источников, или изменение структуры цепи. Тогда при t→+∞ в цепи возникает новый установившийся режим: токи и напряжения станут опять периодическими с тем же общим периодом Т, но графики этих ф-ций будут отличаться от тех, что были до коммутации. Процессы, которые будут происходить в цепи после коммутации, т.е. начиная с t=0, называют переходными процессами
Дифференциальное ур-е переходного процесса – так мы будем называть диф-е ур-я для некоторого выделенного нами тока ветви или напряжения на элементе.
Эти ур-я составляют для цепи, возникшей после коммутации.
Делается это так:
а) записывают полную сис-му ур-й по 1-му и 2-му з-нам Кирхгофа для данной цепи.
б) исключая последовательно из сис-мы неизвестные кроме 1-ой получают искомое ур-е. будет выглядеть ток(искомой величиной здесь будем считать ток i в некоторой ветви):
- дифф ур-е переходного процесса
(i= 
- коэфф ур-я (некоторые числа, котор выражаются через параметры эл-тов цепи)
-свободный член(вид этой ф-ции определяется имеющимися в цепи источниками)
Натуральное число n наз-ся порядком дифф ур-я.
Тип этого дифф ур-я:
- обыкновенное
- линейное
- с пост коэфф
- неоднородное(правая часть отлична от 0, если =0, то ур-е наз-ся однородным).
Рассмотрим на примере как получается такое ур-е:
Для цепи после коммутации имеем:
Дифф-ем 3-е ур-е получим новую сис-му:
Составим ур-е для тока 
, подставляя в 1-е ур-е из 3-го ток 
получим новую сис-му:
Из 2-го ур-я найдём ток 
:
;
После дифф-я этого ур-я будем иметь:
Подставим и 
в 1-е ур-е.
После преобразований получим такой итог:
- дифф-е ур-е переходного процесса(для тока )
3.2 постановка задачи Каши для линейного дифф ур-я с пост.коэфф. начальные условия. Проблема пересчета начальных условий от t=-0 к t=+0. Правила коммутации.
Дифф-е ур-е переходного процесса
(1)
имеет бесконечно много решений. Добавим к нему начальные условия – значения искомой ф-ции и ее первых производных до (n-1) порядка включительно при t=0:
(2) некоторые заданные числа(откуда их взять? см ниже!)
Дифф ур-е (1) с начальн условием (2) наз-ся задачей Каши для данного ур-я. Как известно, эта задача имеет единственное решение.
Построив это решение, мы решим задачу о переходном процессе.
Как построить это решение мы рассмотрим в след п., а сейчас вычислим как работа пост 
, 
и т.д., входящие в нач условие (2). Прежде всего отметим, что мы должны различать знач-я ф-ций при t→-0(в пределе к о слева до коммутации) и при t→+0(в пределах к 0 справа после коммутации).
Дифф ур-е процесса (1) будет выполняться, начиная с момента t=+0, поэтому в начальных условиях (2) на самом деле подразумевается момент t=+0.
Но известным состоянием цепи явл-ся ее состояние при t=-0, поэтому возникают проблемы пересчета состояния цепи от момента t=-0 к моменту t=+0. При таком подсчете важными оказываются правила коммутации.
Сформулируем 1-ое правило. Рассмотрим подключение RC цепи к источнику пост напряжения
Предположим, что в момент коммутации напряжение на конденсаторе изменяется мгновенно, т.е. ф-ция при t=0 
(t) имеет разрыв 1-го рода.
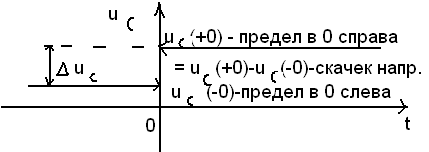
Чтобы увидеть проблему заменим мгновенное изменение напряжения быстрым изменением за время △t
Тогда по 2-му з-ну Кирхгофа для нашей цепи получим:
(3), где
-как производная линейной ф-ции, 
-const, 
→∞=>∞ при 
→0
Мы видим, что при →0 выполнить рав-во (3) невозможно, т.е. мы приходим к противоречию со 2-м з-ном Кирхгофа.
Отсюда мы получаем 1-е правило коммутации:
Напряжение на конденсаторе мгновенно изменяться не может:
Аналогично выводится 2-е правило коммутации:
Ток через катушку индуктивности мгновенно измениться не может:
Решение задачи Каши. Имеем при t>0 задачу Каши для обыкновенного линейного неоднородного дифф-го ур-я порядка n с пост коэфф.
n=2
(1), t>0 исходное неоднородное ур-е(после коммутации)
1-я производная 
(2)наход-ся по известному сост-ю цепи при t=-0 с помощ з-нов коммут
Имеем ввиду +0! Порядок производной