Максимальное, среднее и среднеквадратичное отклонение.

ЛЕКЦИЯ № 13. 16.05.2017

Разложение в ряд Лорана с помощью геометрической прогрессии.

Пример. Разложить функцию :

а) в ряд Лорана в кольце

б) во внешней области

в) в ряд Тейлора в круге .

Во-первых, если центр кольца 0, а точки разрыва и , то есть 3 области: , , .

Чертёж:

кольцо, расположенное между двумя точками разрыва, так, чтобы ни одна из низ не была внутри кольца.

Разложим на простейшие дроби. Это действие необходимо в любом случае, независимо от того, в каком множестве надо получать разложение в ряд.

= = система: = .

1) Для разложения в ряд Лорана в кольце, надо вынести за скобку иногда константу, а иногда , чтобы всегда получалось что-то меньшее 1.

Из условия следует и , то есть в знаменателе можно получать и , но нельзя и .

= =

теперь в каждом случае получено выражение вида котрое и является суммой геометрической прогрессии, и его можно превратить в бесконечную сумму по формуле .

= =

2) Теперь разложим в ряд во внешней области, которую, впрочем, можно также считать кольцом типа . Здесь причём автоматически выполнено также и , т.е. надо получать в знаменталелях выражения и , и в итоге в ответе будут только отрицательные степени.

= = =

в данном случае их можно и объединить, т.к. в каждом слагаемом есть одинаковые степени.

= . В этом ряде Лорана есть только главная часть.

3) Если требуется разложить в ряд в круге, то это получится ряд Тейлора, там наоборот, в обеих дробях надо выносить константу, чтобы было и .

= = =

= .

Пример (со сдвигом центра)

Разложить функцию в ряд Лорана по степеням .

Решение. Центр в точке 1, тогда расстояние до ближайшей особой точки равно 3, а до второй 4. Получается, что кольцо, где будет ряд, для этой задачи: .

Разложение на простейшие дроби то же самое, .

Но после этого надо отделить выражение .

= далее в соответствии с неравенствами надо вынести за скобку в одной дроби константу, а в другой .

= =

= .

Объединить их нельзя, так как в одной части отрицательные степени, а в другой части положительные, это главная и правильная часть ряда соответственно.

Ряды Фурье.

Скалярное произведение функций.

Вспомним скалярное произведение векторов .

Для функций можно построить обобщение. Если заданы 2 функции , то очевидно, их можно умножить в каждой точке. Затем все эти произведения надо проинтегрировать, так как точек на интервале бесконечное количество. Получается как бы бесконечное количество координат.

Итак, определим скалярное произведение пары функций на интервале по формуле: .

Можно считать, что это верно и на отрезке , ведь две граничные точки не влияют на величину интеграла.

Пример. Найти скалярное произведение и на интервале (0,1).

Решение. = = .

Свойства скалярного произведения, которые легко следуют из свойств линейности интеграла:

Вспомним, что для векторов есть понятие модуля,

. Аналогичное понятие для функций называется нормой функции:

Очевидно, что этот квадратный корень существует, ведь , а значит и .

Ортогональные функции.

Две функции называются ортогональными на интервале , если , то есть .

Здесь нет такого простого геометрического смысла, как в случае перпендикулярных векторов, для функций ортогональность значит, что произведение функций где-то больше, а где-то меньше нуля так, чтобы эти части компенсировались и уничтожились при интегрировании.

Пример. Доказать, что функции , ортогональны на интервале .

= = = = 0.

Замечание. Если одна из функций в произведении тождественно равна 0, то интеграл очевидно, равен 0. Поэтому тождественный 0 это ортогональная всем функция.

Ортогональные системы. Если любая пара функций в системе ортогональна, то система называется ортогональной.

ортогональна, если для любых .

Система функций на отрезке :

ортогональна, её подробно рассмотри позже, с помощью неё как раз и строятся тригонометрические ряды Фурье.

Формулы коэффициента (Фурье) разложения по ортогональной системе: или .

Доказательство. Пусть функция представлена в виде суммы: найдём коэффициенты.

Можно скалярно домножить на . Получим

среди этих слагаемых, лишь одно отлично от нуля, ведь система ортогональна, и при будет .

Тогда , тогда то есть .

Можно записать и с помощью интегралов: .

Аналогичное равенство верно и для векторов: .

Максимальное, среднее и среднеквадратичное отклонение.

Чтобы исследовать взаимосвязь 2 функций, а именно, удаление их графиков друг от друга, можно использовать такую величину:

называемую «равномерным», или максимальным, отклонением между графиками. Однако это не совсем точно характеризует взаимосвязь пары функций, ведь они могут идти очень близко, а затем удалиться на коротком интервале, а отклонение будет считаться большим. Например, как на чертеже:

Вместо этого можно рассматривать среднее значение модуля разности, и это уже более точная оценка.

- среднее отклонение.

Но чтобы посчитать интеграл от модуля, надо искать точки пересечения и разбивать интервал на части. Чтобы избежать этих громоздких вычислений, можно рассматривать такую величину:

среднеквадратичное отклонение между и . Когда среднее стремится к 0, то и среднеквадратичное тоже, и хотя они не прямо пропорциональны, но минимальное значение одной из этих величин достигается при тех же условиях, что и у другой.

Если домножить функции из системы на какие-то коэффициенты, то получится выражение многочлен по ортогональной системе.

Теорема. Среднеквадратичное отклонение между и минимально коэффициенты (совпадают с коэффициентами Фурье).

Доказательство. минимально тогда и только тогда, когда минимально, так что мы можем рассмотреть просто интеграл от квадрата разности, то есть величину . Во-первых, она по построениею больше или равна 0. Рассмотрим её подробнее:

= применим свойства скалярного произведения, будет так:

Но от двойной суммы где (n+1)² слагаемых, фактически остаётся только (n+1) так как при несовпадении номера, скалярные произведения 0, ведь это ортогональная система.

преобразуем 2-е слагаемое по формуле .

теперь прибавим и вычтем такое слагаемое, чтобы образовать разность квадратов:

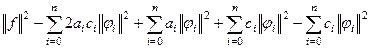Это выражение минимально, когда разность равна 0, то есть в точности, когда что и требовалось доказать.

Отсюда следует неравенство Бесселя:

При получается равенство , которое называется уравнением замкнутости.

Аналоги в векторных пространствах: если рассмотреть неполную сумму квадратов координат какого-то вектора, то очевидно, она меньше, чем квадрат его модуля. Так, для вектора из 3 координат

, . Так и здесь, если рассматривать не всю систему функций, а всего лишь до номера n то получим неравенство, а если всю - то равенство.

Кстати, с помощью скалярных произведений и норм можно доказать аналог теоремы Пифагора для систем функций.

Если ортогональные функции, то:

для векторов такое равенство означало,что квадрат гипотенузы равен сумме квадратов катетов.

1. Доказательства

1. Вывод формул коэффициента (Фурье) разложения по ортогональной системе: или .

2. Доказать теорему: Среднеквадратичное отклонение между и минимально коэффициенты (совпадают с коэффициентами Фурье).

3. Доказать, что если ортогональные функции, то:

= .

2. Определения и формулировки.

Что такое скалярное произведение функий, норма функции.Приведите пример.

Что такое ортогональные фнукции, ортогональная система функций.

Что такое среднее и среднеквадратичное отклонение.

Напишите вид коэффициента Фцрье по произвольной ортогональной системе.

3. Примеры из лекций.