Ьк1. ФКП, действ, мнимая часть, предел, непрерывность
Определение функции комплексной переменной
Рассмотрим две плоскости комплексных чисел: C = { z | z = x + iy } и W = { w | w = u + iv }. Пусть в плоскости С задана область D и задано правило, ставящее в соответствие каждой точке 
определённое комплексное число 
. В этом случае говорят, что на области D определена однозначная функция w = f (z) (или определено отображение 
).
Область D называется областью определения функции, множество 
- множеством значений функции (или образом области D при отображении f.
Действительная и мнимая часть функции комплексной переменной. Так как
w = u + iv, z = x + iy, то зависимость w = f (z) можно записать в виде
w = u + iv = f (z) = f (x + iy) = Re f (x + iy) + i Im f (x + iy). Таким образом, задание комплекснозначной фу нкции w = f (z) комплексной переменной z равносильно заданию двух действительных функций u = u (x, y) = Re f (z), v = v (x, y) = Im f (z) двух действительных переменных х, у.
Предел ФКП.
Опр. Пусть функция w = f (z) определена в проколотой окрестности точки z 0 = x 0 + iy 0. Комплексное число w 0 = u 0 + iv 0 называется пределом функции при 
, если для любой 
-окрестности 
( >0) точки w 0 найдётся такая проколотая 
-окрестность 
точки z 0, что для всех 
значения f (z) принадлежат .
если z 0 - собственная точка плоскости, то для любого >0 должно существовать такое >0, что из неравенства 
следует неравенство 
. Т.о., существование предела функции комплексной переменной равносильно существованию пределов двух действительных функций u (x, y) и v (x, y) двух действительных переменных.
Непрерывность ФКП. Пусть функция w = f (z) определена в окрестности точки z 0 = x 0 + iy 0. Функция называется непрерывной в точке z 0, если:
1. существует 
;
2. 
.
w = f (z) будет непрерывной в точке z 0 = x 0 + iy 0 тогда и только тогда, когда функции u (x, y) и v (x, y) непрерывны в точке (x 0, y 0)
Производная, необхусл, усл. Коши-Римана, аналитичность ф-ции. Формы записи производной
Опр производной. Аналитичность ФКП. Пусть w = f (z) определена, однозначна и принимает собственные значения в окрестности точки 
. Производной функции w = f (z) в точке z называется предел 
. Функция, имеющая конечную производную в точке z, называется дифференцируемой в этой точке.
Опр. Однозначная функция называется аналитической (регулярной)в точке z, если она дифференцируема в некоторой окрестности этой точки.
Однозначная функция называется аналитическойв области D, если она аналитична в каждой точке этой области.
Условия Коши-Римана
Для того, чтобы функция w = f (z) = u (x, y) + iv (x, y) была дифференцируема в точке z = x + iy, необходимо и достаточно, чтобы функции u (x, y) = Re f (z) и v (x, y) = Im f (z) были дифференцируемы в точке (х, у), и чтобы в этой точке выполнялись соотношения
.
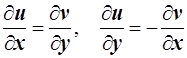Производная дифференцируемой функции может находиться по любой из формул 
, эти равенства следуют из условий Коши-Римана. При вычислении производных можно пользоваться всеми правилами действительного анализа: 
(в точках, где 
.
док-ть регулярность суммы, частного, произведения регулярной ф-ции и сложной ф-ции, восстановление ф-циипо известной мнимой ф-ции
Дифференцируя первое соотношение Коши-Римана 
по переменной х, второе соотношение 
по переменной у, получим 
, т.е. 
(
- оператор Лапласа), т.е. u (x, y) - гармоническая функция. Дифференцируя первое соотношение Коши-Римана по переменной у, второе соотношение по переменной х, получим 
, т.е. 
, т.е. v (x, y) - тоже гармоническая функция. Пара гармонических функций, связанных соотношениями Коши-Римана, называется сопряжёнными функциями.
Для любой гармонической в односвязной области D функции u (x, y) существует единственная (с точностью до постоянного слагаемого) сопряжённая с ней гармоническая функция v (x, y), т.е. такая функция, что w = f (z) = u (x, y) + iv (x, y) - аналитическая функция; и наоборот, для любой гармонической v (x, y) существует сопряжённая с ней гармоническая u (x, y).
Пусть, например, дана u (x, y), обозначим 
. Эти функции удовлетворяют условию 
, т.е. векторное поле 
потенциально. Функцию v (x, y) можно найти теперь из системы 
.