Нули аналитической функции.

Определение. Точка а называется нулём порядка k аналитической функции f (z), если

, но .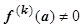

13. Изолированные особые точки.

Определение. Точка а называется изолированной особой точкой функции f (z), если существует окрестность этой точки, в которой f (z) аналитична во всех точках, за исключением точки а.

Рассмотрим разложение функции f (z) в ряд Лорана в окрестности изолированной особой точки а. При этом возможны следующие случаи.

1. Главная часть ряда Лорана отсутствует: .

В этом случае особая точка а называется устранимой.

2. Главная часть содержит конечное число членов:

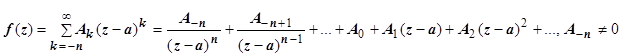
В этом случае особая точка а называется полюсом n -го порядка. Если n =1, полюс называется простым, в остальных случаях - кратным.

3. Главная часть содержит бесконечно много членов. В этом случае особая точка а называется существенно особой точкой.

14. Признаки особых точек по значению .

1. Для того, чтобы особая точка z = a была устранимой особой точкой функции f (z), необходимо и достаточно, чтобы существовал конечный предел .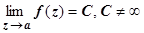

2. Для того, чтобы особая точка z = a была полюсом функции f (z), необходимо и достаточно, чтобы существовал бесконечный предел .

15. Вычеты!

1) Вычет аналитической функции в особой точке. Пусть функция f (z) аналитична в области D за исключением точки a. Разложим f (z) в окрестности этой точки в ряд Лорана:

Коэффициент называется вычетом функции в точке а и обозначается . Если - произвольный кусочно-гладкий замкнутый контур, расположенный в области D и содержащий внутри себя точку а, то, согласно общей формуле для коэффициентов ряда Лорана, .

2) Вычет в устранимой особой точке равен нулю.

Это следует из определения устранимой особой точки: главная часть ряда Лорана отсутствует, все коэффициенты с отрицательными индексами равны нулю, A _-1 = 0.

3) Вычеты в полюсах.

3.1) Если а - простой полюс функции f (z), то .

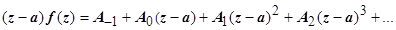Док-во. Простой полюс - полюс первого порядка, поэтому разложение в ряд Лорана начинается с минус первой степени: . Тогда , и .

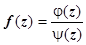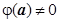3.2) Пусть , где и - аналитические в окрестности точки а функции. Если а - простой нуль функции , и , то .

Док-во. Если а - простой нуль функции , и 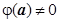, то а – простой полюс функции 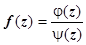. Тогда, по предыдущему утверждению, .

3.3.) Если а - полюс функции f (z) n - го порядка, то .

Док-во. Так как точка z = a - полюс n -го порядка функции f (z), то. . Для того, чтобы удалить особенность в точке а, умножим f (z) на (z – a) ⁿ 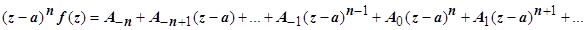. Теперь, чтобы убрать первые члены этой формулы и добраться до A _-1, дифференцируем это произведение n -1 раз: ,

,

………………………………………………………………….,

, , откуда и следует доказываемая формула.

16. Основная теорема о вычетах. Пусть функция f (z) аналитична во всех точках ограниченной замкнутой области , границей которой является контур L, за исключением конечного числа особых точек z ₁, z ₂, z ₃, …, z_n, расположенных внутри L. Тогда .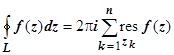

Док-во. Окружим каждую особою точку z_k, k = 1, 2, …, n контуром таким, чтобы все контуры лежали в области D и не пересекались. В области, ограниченной контурами L, , функция аналитична, поэтому по Теореме Коши для многосвязной области

. По определению вычета, , следовательно, , ч.т.д.

17. Бесконечно удалённая особая точка. Будем считать точку особой точкой любой аналитической функции. Точка является изолированной особой точкой аналитической функции w = f (z), если в некоторой окрестности этой точки нет других особых точек этой функции. Для определения типа этой особой точки сделаем замену переменной , при этом точка переходит в точку , функция w = f (z) примет вид . Типом особой точки функции w = f (z) будем называть тип особой точки z ₁ = 0 функции . Если разложение функции w = f (z) по степеням z в окрестности точки , т.е. при достаточно больших по модулю значениях z, имеет вид , то, заменив z на , получим . Таким образом, при такой замене переменной главная и правильная части ряда Лорана меняются местами, и тип особой точки определяется количеством слагаемых в правильной части разложения функции в ряд Лорана по степеням z в окрестности точки 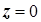. Поэтому

1. Точка - устранимая особая точка, если в этом разложении правильная часть отсутствует (за исключением, возможно, члена A ₀);

2. Точка - полюс n -го порядка, если правильная часть заканчивается слагаемым ;

3. Точка - существенно особая точка, если правильная часть содержит бесконечно много членов.

При этом остаются справедливыми признаки типов особых точек по значению : если - устранимая особая точка, то этот предел существует и конечен, если - полюс, то этот предел бесконечен, если - существенно особая точка, то этот предел не существует (ни конечный, ни бесконечный).

18.Вычет функции в бесконечно удалённой особой точке. Для конечной особой точки z ₁ , где - контур, не содержащий других, кроме z ₁, особых точек, проходимый так, что область, им ограниченная и содержащая особую точку, остаётся слева (против часовой стрелке). Определим аналогичным образом: , где - контур, ограничивающий такую окрестность точки , которая не содержит других особых точек, и проходимый так, что эта окрестность остаётся слева (по часовой стрелке). Таким образом, все остальные (конечные) особые точки функции должны находиться внутри контура . Изменим направление обхода контура : . По основной теореме о вычетах , где суммирование ведётся по всем конечным особым точкам. Поэтому, окончательно, , т.е. вычет в бесконечно удалённой особой точке равен сумме вычетов по всем конечным особым точкам, взятой с противоположным знаком.