- кручение прямого стержня
1. Постановка задачи.
Рассмотрим моделирование напряженного и деформированного состояния в прямом стержне при кручении, т.е. когда из всех внутренних сил только 
. Примеры: валы турбореактивного, турбовинтового и турбовентиляторного двигателей.
Сечение по-прежнему будем считать плоским, что справедливо для круглых сечений и приближенно справедливо для некруглых. Для последних в практических расчетах вводят поправочные коэффициенты для вычисления максимальных напряжений и эффективного полярного момента инерции 
.
Очевидно, что при кручении в сечении возникают касательные напряжения от 
и угловые деформации 
от взаимного сдвига сечений.
Итак, параметры задачи – четыре неизвестные функции от координаты сечения:
- крутящий момент 
(иногда принято обозначать Мz(z)=Мк(z)),
- угол поворота сечения φz(z),
- угловая деформация (z),
- касательное напряжение в сечении 
,
появление которых является следствием действующих внешних нагрузок на определенным образом закрепленный стержень. Ограничимся сосредоточенными крутящими моментами 
и погонными крутящими моментами нагрузками 
, постоянными по величине на длине их действия. Примеры сосредоточенного момента - крутящий момент от зубчатого колеса, момент от одного ряда лопаток турбины. Примеры распределенного момента - момент от нескольких рядов лопаток. Подробнее смотри в конце лекции.
 |
2. Математическая модель
Необходимо сформулировать четыре (по числу параметров) уравнения связи неизвестных функций от z.
Уравнение равновесия получим, рассмотрев равновесие элемента dz. Получаем
. Откуда
. (*)
Для получения физических зависимостей при кручении вернемся к опыту на растяжение и схематизации напряженного состояния.
В принятых координатах в опыте на растяжение имеем линейное напряженное состояние.
Матрица напряжений в главных осях 
, т.е. 
Рассмотрим площадку, повернутую на угол α относительно оси x. При этом проекции нормали 
, а проекции полного напряжения 
(см. в главных осях формулу *** лекция 3) 
Соответственно 
, 
.
Откуда
. (1)
Рассмотрим возникшие угловую деформацию (сумма углов поворота -составляющих изначально прямого угла)
.
Продольная деформация 
.
Поперечная деформация 
.
Спроектируем контур ABLB'A на нормаль n-n к отрезку AB’. Получаем
С учетом малости 
получаем
.
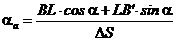С учетом выражений для деформаций: 
, 
.
Для второго отрезка поворотом на 90о получаем
,
,
и, соответственно,
.
Сравнивая последнее выражение с формулой (1) для касательных напряжений, получаем закон Гука при сдвиге -искомое физическое уравнение
,
т.е. 
(**)
где модуль сдвига
(2)
выражается через коэффициент Пуассона и модуль Юнга.
Теперь, используя гипотезу плоских сечений, рассмотрим кольцевой элемент круглого сечения с текущим радиусом 
бесконечно малой толщины 
, длиной dz и площадью dA.
Приравнивая длину дуги BB' из двух треугольников (
), получаем с учетом закона Гука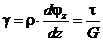 
. откуда
. (3)
Элементарный крутящий момент (
)
и, интегрируя по площади сечения, получаем
.
Для круга 
.
Откуда
, (***)
Подставляя (3) в (***) получаем касательные напряжения
, (****)
которые линейно распределены по высоте сечения.
Задача фактически сводится к решению системы двух линейных дифференциальных уравнений
(*****)
при соответствующих граничных условиях – математическом описании закрепления концов стержня.
По оставшимся двум формулам можно вычислить напряжения и угловую деформацию и провести расчет на прочность.
Матрица напряжений в принятых осях
дает инварианты НС 
и, соответственно, главные напряжения - решение характеристического уравнения матрицы (
)
Напряженное состояние - " чистый сдвиг ".
Условие прочности по гипотезе касательных напряжений:
.
По энергетической гипотезе
.
Как видно, разница существенна. Больший запас дает первый вариант.
Таким образом, анализ напряженного и деформированного состояний сводится к решению системы (*****).
3. Решение задачи и расчет на прочность.
Сравнивая математические модели кручения и растяжения, видим полную аналогию вплоть до обозначений. Поэтому как аналитическое, так и численное решение для кручения получаем из решения для растяжения заменой соответственно:
.
Согласно (****) максимальные касательные напряжения возникают на поверхности тела. Например, для трубчатого сечения внутренним диаметром d, толщиной стенки t и внешним диаметром D
, где 
, 
и максимальное касательное напряжение в сечении
где 
- называют моментом сопротивления при кручении.
В итоге расчет на прочность сводится к проверке условия
по всей длине стержня.
* Сравним расход металла для сплошного (диаметром Dв)и трубчатого валов внешним диаметром Dт и толщиной стенки t. Приравнивая моменты сопротивления (условие равнопрочности) получаем 
и соотношение площадей сечений 
. Результаты расчетов иллюстрируются графиком:
Трубчатый вал позволяет экономить вес конструкции по мере уменьшения толщины стенки. Уменьшение последней при поперечном изгибе ограничено касательными напряжениями по Журавскому, а при чистом кручении - устойчивостью формы поперечного сечения.
Для некруглого сечения используют Wk, приводимое в справочниках, которое вычисляется численно или определяется экспериментально.
Например, для прямоугольного сечения высотой 
и шириной 
, 
и в справочнике приводится таблица
| h/b | 1,5 | ∞ | ||||
| α | 0,208 | 0,231 | 0,246 | 0,282 | 0,307 | 0,333 |
| β | 0,141 | 0,196 | 0,229 | 0,281 | 0,307 | 0,333 |