Эллиптические уравнения в частных производных

Лабораторная работа №2

Тема: Численное решение дифференциальных

Уравнений в частных производных.

Цель работы: Изучение вычислительных возможностей пакета MathCAD для решения методом сеток некоторых уравнений математической физики.

Теоретические сведения.

Дифференциальные уравнения в частных производных требуют нахождения функции не одной, как для ОДУ, а нескольких переменных. Эти уравнения включают в себя производные по различным переменным (частные производные). Уравнениями в частных производных описывается множество разнообразных физических явлений, и с их помощью можно с успехом моделировать самые сложные явления и процессы (диффузия, гидродинамика, квантовая механика, экология и т. д.). MathCAD имеет ограниченные возможности по отношению к уравнениям в частных производных. С помощью его встроенных функций можно решать лишь некоторые из частных случаев. С помощью двух встроенных функций multigrid и relax можно решить только простейшие случаи уравнения Пуассона.

Эллиптические уравнения в частных производных

К исследованию такого уравнения приводит рассмотрение задач об электрических и магнитных полях, о стационарном тепловом состоянии, задач гидродинамики, диффузии и т. д. Рассмотрим решения уравнения Пуассона и его однородной формы - уравнения Лапласа.

Решение уравнения Пуассона будем искать в некоторой ограниченной области

(1)

(1)

Граничные условия:

(2)

где f, f₁, f₂, f₃, f₄ - заданные функции (задача, состоящая в решении эллиптического уравнения при заданных значениях искомой функции на границе расчётной области, называется задачей Дирихле.).

Построим в области равномерную прямоугольную сетку с шагами h и l по х и y соответственно:

Искомая функция 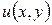с помощью метода сеток (метода конечных разностей) будет представлена множеством своих приближенных значений в узлах сетки Заменим производные конечно-разностными отношениями:

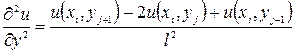, при этом ДУ (1) заменится конечно-разностным уравнением (3).

Аппроксимируем дифференциальную задачу (1) - (2) на шаблоне “крест” (Рис. 1), в результате получаем неявную трехслойную разностную схему (3):

Рис. 1 Шаблон аппроксимации уравнения Пуассона "крест".

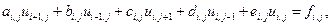(3)

где

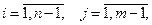
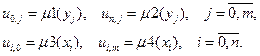
Для решения уравнения Пуассона в Mathcad используется функция relax

relax (a, b, c, d, e, f, u, rjac)

Возвращает квадратную матрицу решения уравнения Пуассона. Здесь a,b,c, d, e - квадратные матрицы одинакового размера, содержащие коэффициенты уравнения (3); f - квадратная матрица, содержащая значения правой части уравнения (3) в каждой точке области W, в которой ищется решение; u - квадратная матрица, содержащая граничные значения решения на границе области и начальное приближение для решения внутри области; rjac - число между 0 и 1, которое управляет сходимостью алгоритма.

При f = 0 получаем уравнение Лапласа:

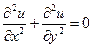
(4)

Если для уравнения Лапласа в области ввести сетку с равным шагом по осям х и y, то разностная схема (3) существенно упрощается

(5)

 

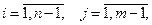
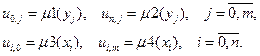
Решение уравнения Лапласа с помощью функции relax показано ниже.

 

Контрольный пример.

Требуется найти распределение температуры в квадратной пластине, для которой заданы граничные условия:

 

Распределение температуры описывается уравнением Лапласа:

Решение.

1. Введем на пластине равномерную сетку с расстоянием между узлами h.

 

 

Сетка содержит 25 узлов, в 16 из которых температура известна согласно граничным условиям

 

 

 

 

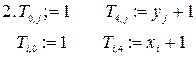
3.Начальное приближение значений температуры в остальных 9 узлах – внутри сетки- положим 0. Таким образом,

 

 

 

 

Стационарное распределение температуры в пластине найдем с помощью разностной схемы (5), используя встроенную функцию relax. (см. решение пункт 4). Схема (5) дает систему 9 линейных алгебраических уравнений с девятью неизвестными значениями Т во внутренних узлах сетки:

 

 

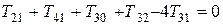
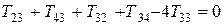
С учетом граничных условий:

 

 

 

4.Задаем матрицы:

 

 

 

Замечание. Распределение температуры Т обладает симметрией соответственно симметрии заданных в примере граничных условий.

5.С помощью команды Graphics Create Contour Plot отобразим найденное распределение температуры в пластине на рис.2

 

 

 

Рис.2

Задание. Найти стационарное распределение температуры в квадратной пластине со стороной 1, описываемое уравнением Лапласа

с краевыми условиямивида

 

 

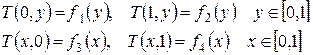
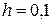
Решать задачу с помощью функции relax.

Для решения задачи построить сетку из 11 узлов по x (i = 0, 1,... 10)и из 11 узлов по y (j = 0, 1,... 10). Отобразить графически с помощью команды Graphics Create Contour Plot стационарное распределение температуры в пластине.

 

Варианты задания

 

№ варианта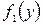
	y 2		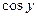x 3
			1 - x 3	x 2
	1 - y 2
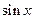
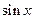
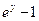
	y 2		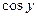x 3	1 + 2 x
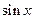
				x 2
	2e y - (1+2e) y 2		1 - x 3
	- 10 y 2 - 8 y + 6	- 10 y 2 - 30 y + 22	9 x 2 + 7 x + 6	9 x 2 - 15 x - 12
	- 7 y 2 - 5 y + 3	- 7 y 2 - 21 y + 13	6 x 2 + 4 x + 3	6 x 2 - 12 x - 9
				x 2 + 3 x + 4
	- y 2 - 5 y	4 + 5 y - y 2	x 2 + 3 x	5 x - 4
	3 - 7 y	7 - 6 y	4 x + 3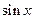
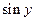