Рассмотрим задачу о распространении тепла в стержне, концы которого поддерживаются при нулевой температуре. Стержень считаем однородным и тонким, так, что d<<l, где d – диаметр стержня, l – его длина. Таким образом, сечение стержня считается настолько малым, что всем точкам сечения в каждый момент времени можно приписать одну температуру. Это означает, что 
, где ось 
направлена вдоль стержня. Боковая поверхность стержня предполагается изолированной от окружающей среды.
В начальный момент времени 
задано распределение температуры вдоль стержня, характеризуемое функцией 
. Указан также тепловой режим, поддерживаемый на концах стержня – считаем температуру на его концах равной нулю. Задача состоит в отыскании решения уравнения теплопроводности
, 
, (10)
при граничных условиях
, 
(11)
и при начальном условии
, (12)
где – непрерывна, имеет кусочно-непрерывную производную и удовлетворяет условиям согласования с требованиями (11) 
Метод разделения переменных, называемый также методом Фурье, заключается в следующем:
1. Ищем частные решения уравнения (10) в виде
. (13)
2. Подставляя (13) в (10) получаем уравнение
.
Разделив обе части полученного уравнения на 
из (13), имеем
. (14)
Постоянная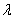 
, называемая постоянной разделения, появилась в (14) из следующих соображений: левая часть в (14) зависит только от переменной 
, правая – только от переменной 
, и эти части должны быть равны при всех значениях и . Поэтому оба отношения в (14) равны постоянной. Приравнивая каждое отношение в (14) постоянной, получим два обыкновенных дифференциальных уравнения для функций 
и 
:
(15)
(16)
3. По условию задачи функция должна удовлетворять краевым условиям вида (16). Из (18) и (16) получаем условия для функции
, 
.
Таким образом, для функции получили задачу: требуется найти не равные тождественно нулю решения краевой задачи
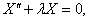
, , (15’)
а также числовые значения параметра, при которых существуют ненулевые решения задачи (15), (15’).
Поставленная задача называется задачей Штурма-Лиувилля. Указанные числовые значения 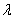называются собственными значениями (числами) краевой задачи, соответствующие этим λ ненулевые решения – собственными функциями.
Найдем собственные числа краевой задачи (15), (15’). Рассмотрим возможности:
Пусть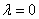 
. Тогда общим решением уравнения (15) будет являться функция
.
При 
и 
, имеем
, 
, 
Следовательно, 
, поэтому 
и начальное условие (12) не будет выполняться.
Пусть 
. Тогда общее решение уравнения (15) имеет вид
.
При и , имеем
, 
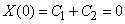систему двух однородных алгебраических уравнений, определитель которой не равен нулю. Поэтому 
, . И в этом случае условие (17) не удовлетворено.
Рассмотрим случай 
. В этом случае корни характеристического уравнения, соответствующего уравнению (15), равны 
, т.е. мнимые числа.
Как известно из курса теории дифференциальных уравнений, общее решение уравнения (15) имеет вид
. (17)
При получаем 
. При имеем
, 
, 
, (18)
где 
. Подставляя (18) в (17), получаем
. (19)
Входящие в формулу (19) функция и постоянная снабжены индексом, поскольку их значения зависят от 
.
Формула (18) определяет собственные числа, а формула (19) – собственные функции краевой задачи, соответствующие этим собственным числам.
4. Подставляя в уравнение (16) вместо 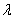собственное значение 
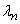для определения функции 
, соответствующей данному собственному значению, получаем уравнение
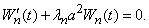(20)
Общее решение уравнения имеет вид
, (21)
где 
- произвольные постоянные.
Итак, все функции
(22)
удовлетворяют уравнению теплопроводности (10) и граничным условиям (11) при любых значениях и любых постоянных 
. Но начальному условию (12) функции (22) в общем случае не удовлетворяют.
5. Требуем, чтобы решение удовлетворяло начальному условию (12). Для этого, учитывая (22), составим ряд
. (23)
Каждый член этого ряда удовлетворяет уравнению (10) и краевым условиям (11).
Предположим, что функция разлагается в равномерно и абсолютно сходящийся ряд Фурье. В силу начального условия, полагая в (23) , получаем
. (24)
Написанный ряд представляет собой разложение функции в ряд Фурье по синусам в промежутке (0,l). Коэффициенты 
находятся по формуле
. (25)
Предполагая, что непрерывна, имеет кусочно-непрерывную производную и обращается в нуль при и , получаем, что ряд (24) с коэффициентами (25) равномерно и абсолютно сходится к (это известно из теории тригонометрических рядов).
Поскольку при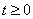 
справедливы неравенства
,
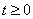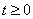то ряд (23) при также сходится абсолютно и равномерно. Поэтому функция (23) непрерывна при , и удовлетворяет начальному и граничному условиям.
Можно показать (мы не останавливаемся на этом), что функция удовлетворяет уравнению (10) и имеет непрерывные производные по и первого и второго порядков соответственно [2]